Рассмотрим пример реализации процесса построения простой после-довательностной схемы
Построим десятичный счетчик с помощью синхронизируемых Т-триггеров. Эта схема содержит четыре таких триггера, выходные сигналы которых формируют кодовый набор, интерпретируемый как десятичная величина в двоично-десятичном коде. Каждый синхроимпульс увеличивает значение кода, которое, достигнув 9, переводится следующим синхроимпульсом в 0. При переходе от 9 к 0 схема выдает выходной сигнал, который указывает на переполнение счетчика: этот сигнал часто называют сигналом переноса.
Первый шаг в процессе проектирования - определение структурной модели и использование ее для идентификации входных и выходных переменных. На рис.10.7 показана подобная модель для десятичного счетчика. В этой схеме, кроме синхросигнала, нет других входных сигналов. Единственным выходным сигналом комбинационной подсхемы является сигнал переноса С.
Если кроме сигнала С вывести также сигналы Q0 - Q3 от всех четырех Т-триггеров, то, используя несколько таких счетчиков, можно получить изображение числа поступивших извне сигналов СИ в двоично-десятичном коде (Д-коде). В таком случае внешний СИ очевидно должен поступать на счетчик, формирующий младшую тетраду кода. Для всех других счетчиков в качестве СИ будет сигнал С предыдущего счетчика. Сигнал С счетчика, формирующего старшую тетраду, является признаком переполнения разрядной сетки, сформированной данной группой этих десятичных счетчиков.
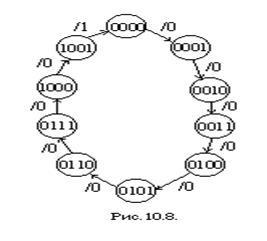
Следующий шаг состоит в построении либо таблицы состояний, либо диаграммы состояний, описывающих поведение схемы. Диаграмма состояний для этого счетчика приведена на рис.10.8. Согласно диаграмме, схема имеет 10 допустимых состояний, последовательность которых есть 0000, 0001, 0010...,1000, 1001, затем следует повторение 0000, 0001 и т.д. Поскольку схема не имеет входов, на ориентированных линях указан лишь текущий выходной сигнал, соответствующий каждому состоянию. Эти значения равны 0 для всех допустимых состояний, за исключением 1001. Таблица 10.1 является соответствующей таблицей состояний. Так как схема не имеет входов, таблица содержит только один внутренний столбец. Отметим, что для шести неиспользованных состояний от 1010 до 1111 следующие состояния не заданы, они обозначены как неопределенные состояния.
Таблицы 2 и 3 являются соответственно таблицей истинности для выхода схемы С и расширенной таблицей истинности для входов триггеров Т3, Т2, Т1, Т0. Выходные значения таблицы истинности и следующие состояния расширенной таблицы истинности получены последовательно по строкам из соответствующих элементов таблицы состояний или соответствующих ориентированных линий на диаграмме состояний. Выходные значения триггеров выбраны такими, чтобы мог осуществляться каждый заданный переход состояний. При определении этих состояний была использована таблица переходов Т-триггера:
Т а б л и ц а 1. Таблица состояний десятичного счетчика
Текущее состояние Следующее состояние
Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0
0 0 0 0 0 0 0 1/0
0 0 0 1 0 0 1 0/0
0 0 1 0 0 0 1 1/0
0 0 1 1 0 1 0 0/0
0 1 0 0 0 1 0 1/0
0 1 0 1 0 1 1 0/0
0 1 1 0 0 1 1 1/0
0 1 1 1 1 0 0 0/0
1 0 0 0 1 0 0 1/0
1 0 0 1 0 0 0 0/1
1 0 1 0 d d d d/d
1 0 1 1 d d d d/d
1 1 0 0 d d d d/d
1 1 0 1 d d d d/d
1 1 1 0 d d d d/d
1 1 1 1 d d d d/d
Т а б л и ц а 2. Таблица переходов Т-триггера
| Текущее состояние Q | Следующее состояние Q | N |
Таблица \3\
| Текущее состояние | Выход | Текущее состояние | Следующее состояние | Вход триггера | ||||||||||||
| Q3 | Q2 | Q1 | Q0 | C | Q3 | Q2 | Q1 | Q0 | Q3 | Q2 | Q1 | Q0 | T3 | T2 | T1 | T0 |
| d | d | d | d | d | d | d | d | d | ||||||||
| d | d | d | d | d | d | d | d | d | ||||||||
| d | d | d | d | d | d | d | d | d | ||||||||
| d | d | d | d | d | d | d | d | d | ||||||||
| d | d | d | d | d | d | d | d | d | ||||||||
| d | d | d | d | d | d | d | d | d |
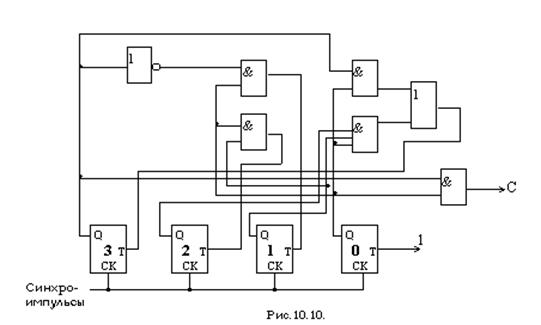
Следующим шагом является получение выражений для выходного сигнала С и входных сигналов триггеров Т3, Т2, Т1 и Т0. На рис. 9 показаны карты, использованные при получении этих минимальных сумм произведений. Логическая схема десятичного счетчика, реализованная в соответствии с этими выражениями посредством вентилей И, ИЛИ, НЕ и четырех синхронизируемых Т-триггеров, приведена на рис.10.10.
| Q1Q0 | Q1Q0 | Q1Q0 | Q1Q0 | |
| Q3Q2 | ||||
| Q3Q2 | ||||
| Q3Q2 | d | d | d | d |
| Q3Q2 | d | d |
T3 = Q3Q0 + Q2Q1Q0
| Q1Q0 | Q1Q0 | Q1Q0 | Q1Q0 | |
| Q3Q2 | ||||
| Q3Q2 | ||||
| Q3Q2 | d | d | d | d |
| Q3Q2 | d |
T2 = Q1Q0
| Q1Q0 | Q1Q0 | Q1Q0 | Q1Q0 | |
| Q3Q2 | ||||
| Q3Q2 | ||||
| Q3Q2 | d | d | d | d |
| Q3Q2 | d | d |
T1 =Q3Q0
| Q1Q0 | Q1Q0 | Q1Q0 | Q1Q0 | |
| Q3Q2 | ||||
| Q3Q2 | ||||
| Q3Q2 | d | d | d | d |
| Q3Q2 | d | d |
T0 = 1
| Q1Q0 | Q1Q0 | Q1Q0 | Q1Q0 | |
| Q3Q2 | ||||
| Q3Q2 | ||||
| Q3Q2 | d | d | d | d |
| Q3Q2 | d | d |
C = Q3Q0
Рис. 9.
Изучение принципов синтеза таких узлов компьютерной техники как различные сумматоры, умножители, шифраторы, дешифраторы, счетки и регистры разного типа и т.д. является своего рода заключительным этапом изучения арифметических и логических основ вычислительной техники. Знания этих принципов безусловно необходимы для будущих специалистов по разработке и эксплуатации вычислительной техники, а также различных автоматизированных устройств.
Однако на практике при синтезе узлов цифровых автоматов, пред-назначенных для реализации достаточно сложных алгоритмов, надо четко и хорошо знать номенклатуру, реализуемые функции и рабочие характеристики современных перспективных интегральных схем средней и большой интеграции. В настоящее время существует достаточно большое число интегральных схем средней и большой интеграции, реализующих различные функции узлов компьютера: триггеры, счетчики, шифраторы, дешифраторы и т.д. Поэтому нет необходимости разрабатывать такие узлы при помощи схем малой интеграции, которые реализуют элементарные логические функци: И, ИЛИ, И-НЕ, НЕ и т.д.
СПИСОК ЛИТЕРАТУРЫ
1. А.Я.Савельев. Арифметические и логические основы цифровых автоматов. М.: Высшая школа. 1980.
2. А.Я.Савельев. Прикладная теория цифровых автоматов. М.:Высшая школа. 1987.
3.Е.Н.Вавилов, Г.П.Портной. Синтез схем электронных цифровых машин. М.: Советское радио. 1963.
4. Г.Н.Соловьев. Арифметические устройства ЭВМ. М.: Энергия. 1978.
5. А.Г.Филиппов, О.С.Белкин. Проектирование логических узлов ЭВМ. М.: Советское радио.1974.
6. Я.Будинский. Логические цепи в цифровой технике. М.: Связь. 1977.
7. Ч.Гилмор. Введение в микропроцессорную технику. М.: Мир. 1984.
8. Я.Чу. Организация ЭВМ и микропрограммирование. М.: Мир. 1975.
9. А.М.Шауман. Основы машинной арифметики. Л.: Из-во Ленинградского университета. 1979.






