Электродвигатели, преобразующие электрическую энергию в механическую, создают вращательное движение; значительная часть машин-орудий также имеет вращающиеся рабочие органы; поэтому представляется целесообразным вывод уравнения движения сделать сначала для случая вращательного движения.
В соответствии с основным законом динамики для вращающегося тела векторная сумма моментов, действующих относительно оси вращения, равна производной момента количества движения:
(5.1)
В системах электропривода основным режимом работы электрической машины является двигательный. При этом момент сопротивления имеет тормозящий характер по отношению к движению ротора и действует навстречу моменту двигателя. Поэтому положительное направление момента сопротивления принимают противоположным положительному направлению момента двигателя, в результате чего уравнение (5.1) записывается в виде:
(5.2)
Уравнение движения привода (5.2) показывает, что развиваемый двигателем вращающий момент 
уравновешивается моментом сопротивления 
на его валу и инерционным или динамическим моментом 
. Где ω - угловая скорость этого звена, рад/с.
Отметим, что угловая скорость 
(рад/с) связана с частотой вращения n (об/мин) соотношением
В уравнении (5.2) принято, что момент инерции привода 
является постоянным, что справедливо для значительного числа производственных механизмов. Здесь моменты являются алгебраическими, а не векторными величинами, поскольку оба момента и действуют относительно одной и той же оси вращения. Правую часть уравнения (5.2) называют инерционным (динамическим) моментом (
), т.е.
(5.3)
Этот момент проявляется только во время переходных режимов, когда изменяется скорость привода. Из (5.3) следует, что направление динамического момента всегда совпадает с направлением ускорения электропривода. В зависимости от знака динамического момента различают следующие режимы работы электропривода:
1) 
, т.е. 
, имеет место ускорение привода при 
, и торможение привода при 
.
2) 
, т.е. 
, имеет место замедление привода при , и ускорение при .
3) 
, т.е. 
, в данном случае привод работает в установившемся режиме, т.е. 
.
Выбор знаков перед значениями моментов зависит от режима работы двигателя и характера моментов сопротивления.
Наряду с системами, имеющими только элементы, находящиеся во вращательном движении, иногда приходится встречаться с системами, движущимися поступательно. В этом случае вместо уравнения моментов необходимо рассматривать уравнение сил, действующих на систему.
При поступательном движении движущая сила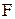 
всегда уравновешивается силой сопротивления машины 
и инерционной силой 
, возникающей при изменениях скорости. Если масса тела 
выражена в килограммах, а скорость 
— в метрах в секунду, то сила инерции, как и другие силы, действующие в рабочей машине, измеряются в ньютонах (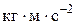
).
В соответствии с изложенным уравнение равновесия сил при поступательном движении записывается так:
. (5.4)
В (5.4) принято, что масса тела является постоянной, что справедливо для значительного числа производственных механизмов.
