Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких возможных ветвей вычислений. Выбор конкретной ветви зависит от выполнения (или не выполнения) заданных условий на значения переменных алгоритма.
Пример 3.2.1. Значение переменной y зависит от значений переменной x и определяется выражением:
(3.2.1)
Выбор одной из двух ветвей вычислений определяется текущим x. На рис. 3.2.1 представлена блок-схема этого алгоритма, хорошо подтверждающая название алгоритма – «разветвляющийся».¨
 |
Рис. 3.2.1. Блок-схема разветвляющегося алгоритма (3.2.1)
Возникает вопрос: какие конструкции необходимы для реализации разветвляющегося алгоритма? Анализ алгоритма (3.2.1) и «программистская интуиция» подсказывают необходимость использования:
· конструкций, проверяющих выполнение заданных условий (чаще гораздо более сложных, чем условие алгоритма (3.2.1));
· конструкций, выбирающих нужную ветвь вычислений в зависимости от результатов проверки заданных условий.
Для проверки заданных условий в MathCAD используется: выражение отношений, логические операции и логические выражения.
Выражением отношений (или просто отношением) называется конструкция вида:
<выр.1> <операция отношения> <выр.2>,
где <выр.1>, <выр.2> – произвольные арифметические выражения, < операция отношения > – любая из следующих операций: 
(здесь вертикальные чёрточки являются разделительным символом при перечислении).
Смысл этих операций понятен и не нуждается в пояснении. Для ввода знаков операций отношений можно использовать палитру Логический (приведённую на рис. 3.2.2) или использовать клавиши, обозначения которых приведены в табл. 3.2.1.
Рис. 3.2.2. Палитра инструментов Логический
Внимание! Не следует путать знак операции сравнения = с похожим знаком вывода значений переменных. Знак операции = имеет больший размер и более жирное начертание.
Таблица 3.2.1
| Знаки операции | Клавиши |
| < | [<] |
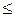
| [Ctrl] + [9] |
| > | [>] |
| [Ctrl] + [0] |
| = | [Ctrl] + [=] |
| [Ctrl] + [3] |
Выражение отношений принимает одно из двух значений: 1 – если заданное отношение выполняется, 0 – в противном случае. Значение 1 можно интерпретировать как значение истина, а 0 – как ложь.
Задание 3.2.1. Пусть значение целой переменной x =3. Определить значение следующих выражений отношений:
. ●
Для проверки более сложных условий используются четыре логические операции, обозначения которых приведены в табл. 3.2.2.
Таблица 3.2.2
| Название операции | Знак |
 Логическое отрицание (NOT)
| |
| Логическое ИЛИ (OR) |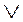 
|
| Логическое И (AND) | 
|
| Исключающее ИЛИ (XOR) |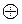 
|
Знаки этих операций вводятся с палитры Логический. Результат выполнения этих операций приведен в табл. 3.2.3.
Таблица 3.2.3
NOT 
| AND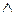 
| OR 
| XOR 
|
| 
| 
| 
|
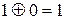
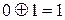
Логическим выражением называется конструкция, состоящая из выражений отношений, логических операций и круглых скобок. Логическое выражение принимает только одно из двух значений: 1 или 0; вычисляется слева направо с учетом приоритета входящих в выражение операций. Наивысший приоритет – круглые скобки, а затем по убыванию: AND, OR и XOR – одинаковый приоритет и самый низкий приоритет выражения отношений.
Задание 3.2.2. Определите порядок вычисления значений логических выражений в документе MathCAD, приведенных на рис. 3.2.3. ●
Рис. 3.2.3. Примеры логических выражений
Для выбора нужной ветви разветвляющегося алгоритма используется конструкция, названная условной функцией if, записываемая в виде:
if (<логическое выражение>, <выр. 1>, <выр. 2>),
где имя функции if вводится с клавиатуры. Если логическое выражение равно 1, то значение функции определяется выр.1, в противном случае – выр. 2. Блок-схема этой функции приведена на рис. 3.2.4.
 |
Рис. 3.2.4. Блок-схема функции if
При программировании разветвляющихся алгоритмов с тремя и более вычислительными ветвями в качестве выр. 1 и выр. 2 вновь может использоваться функция if (см. пример 3.2.1).
Пример 3.2.1. Используя условную функцию if, запрограммировать два разветвляющихся алгоритма.
А. 
Б. 
|
|
Рис. 3.2.5. Реализация разветвляющихся алгоритмов
Конструкции, реализующие эти алгоритмы, показаны на рис. 3.2.5. Для алгоритма Б была определена функция пользователя z (x), а затем был построен ее график.
В MathCAD имеется ряд встроенных функций, которые возвращают результат, зависящий от знака или величины аргумента, и могут использоваться при программировании разветвляющихся алгоритмов. Приведем некоторые из них:
· ceil (x) – наименьшее целое, большее или равное x;
· trunc (x) – целая часть вещественного числа x;
· floor (x) – наибольшее целое, меньшее или равное x;
· round (x, n) – округленное значение вещественного x с точностью до n знаков после десятичной точки;
· Ф(x) – функция Хевисайда – равна 0 при x < 0 и 1 в противном случае;
· sign (x) – функция знака (равна 0 если x = 0; -1, если x <0 и 1, если x >0);
· signum (x) – возвращает 1, если x = 0 и 
в остальных случаях.
