Под структурой данных типа массив понимают однородную структуру однотипных данных, одновременно хранящихся в последовательных ячейках оперативной памяти. Эта структура должна иметь имя и определять заданное количество данных (элементов). Однотипность данных определяет возможность использования циклических алгоритмов для обработки всех элементов массива. Количество итераций цикла определяется количеством элементов массива. Одновременное хранение в памяти всех элементов массива позволяет решать большой набор задач, таких как, поиск элементов, упорядочение и изменение порядка следования элементов.
Доступ к любому элементу массива осуществляется по его номеру (индексу). Поэтому для обращения к элементу массива используют имя_массива(номер элемента), например, А(5).
Массив называется одномерным, если для получения доступа к его элементам достаточно одной индексной переменной.
Рассмотрим простой алгоритм ввода элементов одномерного числового массива A из 9 элементов. В этом циклическом алгоритме условие выхода из цикла определяется значением специальной
 |
 переменной К, которая называется счетчиком элементов массива А (рис.16), эта же переменная К определяет количество итераций циклического алгоритма ввода элементов массива. На каждом шаге итерации переменная К(значение номера элемента массива А) изменяется на 1, то есть происходит переход к новому элементу массива.В дальнейшем, при рассмотрении алгоритмов обработки одномерных массивов в целях устранения дублирования алгоритм ввода элементов массива будем заменять одним блоком, подразумевая, что он реализуется по схеме, циклического алгоритма, представленного на ри- сунке 16.
переменной К, которая называется счетчиком элементов массива А (рис.16), эта же переменная К определяет количество итераций циклического алгоритма ввода элементов массива. На каждом шаге итерации переменная К(значение номера элемента массива А) изменяется на 1, то есть происходит переход к новому элементу массива.В дальнейшем, при рассмотрении алгоритмов обработки одномерных массивов в целях устранения дублирования алгоритм ввода элементов массива будем заменять одним блоком, подразумевая, что он реализуется по схеме, циклического алгоритма, представленного на ри- сунке 16. Пример 9. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.
Пример 9. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.
 |  |  |
Решение. Алгоритм представлен на рисунке 17. В этом алгоритме переменная К - является счетчиком элементов массива, S - сумма элементов массива, она вычисляется по реккурентной формуле S=S+A(K). Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по
схеме алгоритма ввода элементов массива, изображенного на рис.16.
Часто для проверки правильности работы алгоритмов на конкретных наборах данных используют таблицу трассировки. Эта таблица содержит столько столбцов, сколько переменных и условий в алгоритме, в ней мы выполняем действия шаг за шагом от начала до конца алгоритма для конкретных наборов входных данных.
Пример 10. Составить алгоритм поиска элемента с максимальным значением в
одномерном массиве А(1..n) и его таблицу трассировки для значений (3, 7, 0, 9).
Решение. Введем обозначения K- текущий номер элемента, A[K] - текущее значение элемента массива, N=4 количество элементов одномерного массива, M- номер максимального элемента массива, A[M] - значение максимального элемента массива. Основной идеей алгоритма является выполнение сравнения текущего элемента массива A[K] и элемента с максимальным значением A[М],
 |
определенным на предыдущем шаге итерации. По алгоритму изображенному на рис.18 получено максимальное значение для массива (3, 7, 0, 9), процесс и правильный результат поиска которого показаны в таблице 4.
Рис.18. Алгоритм поиска максимального значения в массиве
Таблица 4. Таблица трассировки алгоритма примера 10.
| Номер элемента массива К | Значение элемента А (К) | Номер максимального М | Значение максимальнго А(М) | Проверка А(К)>А(М) | ||
| Нет | ||||||
| да | ||||||
| нет | ||||||
| 4 | 9 | да |
Рассмотрим несколько более сложных алгоритмов, в которых осуществляется изменение порядка следования элементов в одномерном массиве. К таким алгоритмам относят алгоритмы с перестановкой элементов местами, алгоритмы удаления некоторых элементов или циклического переноса некоторых элементов в начало или конец массива.
Основным требованием при составлении алгоритмов обработки массивов является использование минимально необходимых переменных.
Чтобы точнее уяснить постановку задачи следует сначала рассмотреть частные решения для некоторых значений входных данных (провести анализ), затем обобщить полученное решение и определить набор решаемых задач. Составив визуальный алгоритм, его следует проверить на различных наборах исходных данных. Эти наборы исходных данных требуется подбирать таким образом, чтобы при заполнении таблиц трассировок проверить все пути вычислений данного алгоритма от начальной вершины до конечной.
Пример 11. Составить алгоритм решения и таблицу трассировки следующей задачи. В одномерном массиве поменять местами 2-ой нулевой элемент и последний положительный элемент. Применить нисходящее проектирование алгоритма.
Решение. Пусть одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0). Среди этих элементов имеются три нулевых значения, отрицательные и положительные значения. Второй нулевой элемент имеет порядковый номер 6, а последний положительный элемент - номер 3, его значение равно 4. Если поменять местами 2-ой нулевой элемент и последний положительный в исходном массиве (5, 0, 4, -3, -7, 0, -2, -4, 0) то получим новый массив, в котором изменен порядок следования элементов 5, 0, 0, -3, -7, 4, -2, -4, 0.
 |
Основными операциями алгоритма будут: поиск второго нулевого элемента массива, поиск последнего положительного элемента массива и перестановка найденных элементов. Отметим, что для перестановки элементов необходимо знать номера переставляемых элементов. На рис. 19 изображен обобщенный алгоритм решения задачи, который в дальнейшем будет детализирован.
Рис. 19. Обобщенный алгоритм к примеру 11
Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по схеме алгоритма ввода элементов массива, изображенного на рис.16.
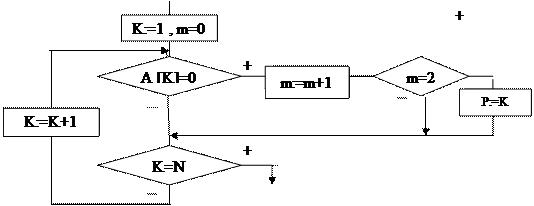 |
Поиск второго нулевого элемента массива будем осуществлять в цикле, проверяя значение очередного элемента на 0. Если очередной элемент равен 0, то для подсчета количества таких элементов используем реккурентную формулу M=M+1. В тот момент времени, когда значение М=2, нам необходимо запомнить номер текущего элемента массива, так как это и есть искомый второй положительный элемент исходного массива. На рис.20 приведен фрагмент алгоритма, реализующего поиск второго нулевого элемента в некотором массиве А из N элементов.
Рис. 20. Фрагмент алгоритма поиска второго нулевого элемента в массиве А, состоящем из N элементов. Здесь К- номер очередного элемента, А(К) - значение очередного элемента, m -количество нулевых элементов, Р- номер второго нулевого элемента в массиве
 |
Поиск последнего положительного элемента массива будем осуществлять аналогично в цикле, запоминая номер очередного элемента, значение которого больше нуля, в дополнительной переменной S. Учитывая тот факт, что после того, как будут просмотрены и проверены на положительность все элементы массива, в переменной S будет храниться номер последнего положительного элемента массива. На рис. 21 представлен фрагмент алгоритма поиска последнего положительного элемента в массиве А.
 |
Рис. 21. Фрагмент алгоритма поиска последнего положительного элемента
Рассмотрим фрагменты алгоритма, приведенные на рис. 20 и 21. Можно заметить, что оба этих фрагмента выполняют поиск под управлением цикла, с одинаковым числом повторений, равным количеству элементов исходного массива N. Поэтому в итоговом алгоритме решения задачи примера 11 вместо композиции этих двух фрагментов в виде двух последовательных циклов можно использовать параллельное выполнение операций поиска под управлением одного цикла, который приведен на рис. 22.
 |
Рис 22. Алгоритм поиска второго нулевого и последнего положительного элементов массива А.
Напомним, что исходный одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0).По условию задачи необходимо поменять местами 2-ой нулевой элемент и последний положительный элемент.
Так как задачи поиска необходимых для перестановки элементов алгоритмически решены (рис. 22), то рассмотрим задачу перестановки элементов.Для реализации перестановки найденных элементов достаточно воспользоваться управляющей структурой следования. Для того, чтобы во время перестановки не потерять переставляемые значения используем дополнительную переменную Q, временно хранящую одно из переставляемых значений элемента массива, в частности, второе нулевое значение.На рис. 23 представлен универсальный алгоритм перестановки двух элементов одномерного массива, имеющих порядковые номера P и S.
 |
Рис. 23.Фрагмент перестановки двух элементов массива, с номерами S и P
 |
Подводя итог для алгоритмического решения примера 11, приведем на рис. 24 алгоритм для вывода элементов преобразованного массива после перестановки найденных элементов.
Рис. 24. Алгоритм вывода элементов массива
 |
Таким образом, процесс проектирование первоначального алгоритма перестановки второго нулевого элемента и последнего положительного элемента в одномерном массиве завершен. Полученный алгоритм представлен на рис.25. Следует заметить, что целью решения примера 11 было показать процесс нисходящего проектирования алгоритма " сверху-вниз " с использованием декомпозиции и метода структурной алгоритмизации. Отметим, что с целью упрощения в полученном алгоритме не рассматриваются ситуации, когда в составе элементов массива отсутствуют положительные значения или нулевые значения в количестве большем одного.
 | |||
 | |||
 |
Рис.25. Алгоритм перестановки второго нулевого и последнего положительного элемента в одномерном массиве
Для проверки правильности работы полученного алгоритма составим таблицу трассировки для одномерного массива из 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0), приведенных в примере 11. Напомним, что заполнение таблицы происходит по строкам. Считаем, что все начальные значения числовых переменных равны 0.
В таблице 5 выполнена трассировка фрагмента поиска второго нулевого и последнего положительного элементов (их номеров), а в таблице 6 выполнена трассировка следующего фрагмента алгоритма по перестановке в массиве найденных элементов, где K- текущий номер элемента, A[K] - текущее значение элемента массива, М- количество нулей, обнаруженных в массиве при анализе очередного элемента, P- номер второго нулевого элемента массива, S- номер последнего положительного элемента массива, A[S] - значение последнего положительного элемента массива, A[P] - значение второго нулевого элемента массива.
Таблица 5.Таблица трассировки операций Таблица 6. Таблица трассировки
поиска второго нулевого элемента и перестановки найденных элемен-
последнего положительного тов массива
| К | Входной массив А(К) | M | М=2 | Р | S | A(P) А(6) | Q | А(S) А(3) | Выходной массив А(К) | |
| Нет | ||||||||||
| Нет | ||||||||||
| -3 | -3 | |||||||||
| -7 | -7 | |||||||||
| Да | ||||||||||
| -2 | -2 | |||||||||
| -4 | -4 | |||||||||
| Нет |
Пример 12. Составить алгоритм удаления в одномерном массиве элемента с максимальным значением.
Решение. Анализ постановки задачи позволяет выделить две последовательно решаемые задачи: поиск элемента с максимальным значением и удаление этого значения из массива. Алгоритм первой задачи был рассмотрен ранее в примере 10 (рис.18). В этом алгоритме был определен номер максимального значения М, а максимальное значение определялось как А(М). Удаление элемента из массива приводит к уменьшению количества элементов массива за счет их перемещения на позицию удаляемого. Например, требуется удалить максимальное значение в массиве (2,4,13,5,7). Максимальное значение в этом примере равно 13. После удаления количество элементов данного массива уменьшится на 1 и станет равным 4, а массив примет вид (2,4,5,7). Таким образом, можно сделать вывод, что для удаления элемента из массива необходимо знать его номер, например М, удаление производится путем сдвига на одну позицию влево всех следующих за удаляемым элементов А(М)=А(М+1), этот сдвиг должен осуществляться под управлением цикла. Цикл завершит свою работу, когда последний элемент массива сдвинется на место предпоследнего элемента.
После приведенных рассуждений и используя алгоритмическое решение примера 10, изображенное на рис.18, составим алгоритм удаления элемента с максимальным значением из одномерного массива из N элементов (см. рис.26).
 |
Рис. 26. Алгоритм удаления элемента с максимальным значением
К - номер очередного элемента, М- номер элемента с максимальным значением, N-1 - уменьшенное в результате удаления одного элемента количество элементов массива А, A [K]: =A [K+1] - удаление путем сдвига влево следующих за удаляемым элементов на одну позицию.






