Интегральная оценка представляет собой определенный интеграл от некоторой функции переходной составляющей ошибки.
Обычно интегральные оценки применяют для следящих систем, которые являются астатическими. Для астатической системы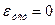 
, 
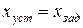
Переходная составляющая ошибки 
 |
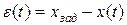
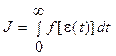
Простейшая интегральная оценка
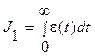
Для апериодических переходных процессов
 |
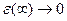
Система стремится к идеальной, если 
Другими словами качество переходного процесса тем лучше, чем меньше площадь, ограниченная кривой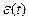 
Для колебательного переходного процесса линейные оценки качества неприменимы, т.к. площади ограниченные кривой и осью абсцисс складываются с учетом знака. При неизвестном характере затухания переходного процесса пользуются следующими оценками:
 | |||
 |
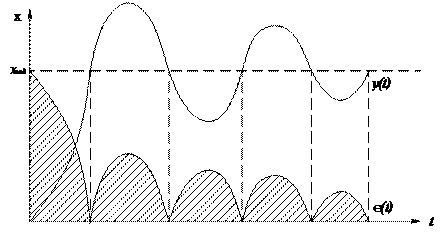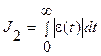
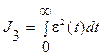– интегральный квадратичный критерий
При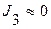 
переходная функция будет представлять собой ступенчатый сигнал
В результате приближения переходного процесса к идеальному (ступенчатому) получается, что увеличивается скорость изменения входной величины.
Поэтому при оценке переходного процесса по интегральному квадратичному критерию сильноколебательный процесс может оказаться лучше, чем неколебательный, а это не всегда является правильным. Интегральный квадратичный критерий можно улучшить, если учитывать не только ошибку 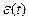, но и скорость ее изменения 
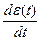. Такой оценкой является следующий интеграл:
– улучшенный квадратичный критерий
t – постоянная времени
Минимальное значение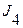 
соответствует приближению переходного процесса не к ступенчатому, а к некоторому экспоненциальному процессу с постоянной времени t
|
Используются и более сложные интегральные оценки.
Недостатками интегральных оценок являются невозможность получения прямых показателей качества и высокая сложность вычислительных процедур. Достоинство – это возможность выразить интегральные оценки как функции параметров системы и, воспользовавшись известными методами поиска экстремума, определить значения этих параметров, дающие минимум избранной оценке.
