Параметров нефтепровода

Расчеты выполняются в следующей последовательности.

· Определяется средневзвешенная температура грунта вдоль трассы нефтепровода

(2.1)

где – температура грунта на глубине заложения нефтепровода для участка длиной l_i, К.

· По формулам (1.1)-(1.8) вычисляются параметры перекачиваемой нефти ρ_р и ν_р при расчетной температуре.

· Вычисляется расчетная часовая пропускная способность нефтепровода

(2.2)

где N _p – расчетное число суток работы нефтепровода, N _p = 350 сут.

· В соответствии с расчетной часовой пропускной способностью нефтепровода Q _ч выбираются основные насосы насосных станций так, чтобы выполнялось условие

(2.3)

где Q _ном – подача выбранного типа насосов при максимальном КПД, м³/ч.

Если условие (2.3) выполняется для двух типов насосов, то дальнейшие расчеты выполняются для каждого из них. Например, при Q _ч = 5800 м³/ч для дальнейших расчетов по вариантам принимаются насосы типов НМ 5000-210 и НМ 7000-210. Аналогично подбираются подпорные насосы.

· Рассчитывается рабочее давление на выходе головной насосной станции

(2.4)

где g – ускорение свободного падения, g = 9,81 м/с²; m _мн – число последовательно включенных магистральных насосов, обычно m _мн = 3; h _мн, h _пн – напоры соответственно магистрального и подпорного насоса при расчетной производительности Q _ч, м.

Найденная величина P должна быть меньше допустимого давления P _д, определяемого из условия прочности запорной арматуры. Запорная арматура на нефтепроводах рассчитана на давление P _д = 6,4 МПа. Если условие

(2.5)

не выполняется, то необходимо либо уменьшить число магистральных насосов, либо воспользоваться сменными роторами меньшего диаметра.

· Ориентировочное значение внутреннего диаметра вычисляется по формуле

(2.6)

где w ₀ – рекомендуемая ориентировочная скорость перекачки, определяемая из графика (рис.2.1).

Рис.2.1. Зависимость рекомендуемой скорости перекачки

от плановой производительности нефтепровода

Ориентировочное значение внутреннего диаметра магистральных нефтепроводов может быть найдено и по формуле, полученной А.А.Коршаком и Е.А.Любиным,

(2.7)

где Q _ч – часовая производительность нефтепровода, м³/ч.

· По значению D ₀ принимается ближайший стандартный наружный диаметр D _н. Значение D _н можно также определять из параметров магистральных нефтепроводов. Для дальнейших расчетов и окончательного выбора диаметра нефтепровода назначаются несколько (обычно три) смежных стандартных диаметра.

Параметры магистральных нефтепроводов:

Производительность G_r, млн.т./год	Наружный диаметр D _н, мм	Рабочее давление Р, МПа
0,7-1,2		8,8-9,8
1,1-1,8		7,48,3
1,6-2,4		6,67,4
2,2-3,4		5,46,4
3,2 … 4,4		5,4-6,4
4,0-9,0		5,3-6,1
7,0-13,0		5,1-5,5
11,0-19,0		5,6-6,1
15,0-27,0		5,5-5,9
23,0-50,0		5,3-5,9
41,0-78,0		5,1-5,5

· Для каждого значения принятых вариантов стандартных диаметров вычисляется толщина стенки трубопровода

(2.8)

где Р – рабочее давление в трубопроводе, МПа; n_p – коэффициент надежности по нагрузке; R ₁ – расчетное сопротивление металла трубы, МПа,

;

(2.9)

σ_вр – предел прочности, МПа; m _y – коэффициент условий работы; k ₁ – коэффициент надежности по материалу; k _н – коэффициент надежности по назначению.

Коэффициенты n_p, m _y, k ₁, k _н находят из СНиП 2.05.06-85 [3].

При наличии продольных осевых сжимающих напряжений толщина стенки определяется из условия

(2.10)

где ψ₁ – коэффициент, учитывающий двухосное напряженное состояние труб,

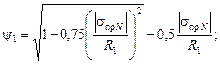
(2.111)

σ_пр _N – абсолютное значение продольных осевых сжимающих напряжений, вычисляемое по действующим расчетным нагрузкам и воздействиям с учетом упруго-пластической работы металла труб в зависимости от принятых конструктивных решений,

(2.12)

α – коэффициент линейного расширения металла трубы, α = 12·10^-⁶ град^–1; Е – модуль упругости металла (сталь), Е = = 2,06·10⁵ МПа; Δ Т – расчетный температурный перепад; d – внутренний диаметр трубы, м.

Абсолютное значение максимального положительного Δ Т ₍₊₎ или отрицательного Δ Т _(–) температурного перепада, при котором толщина стенки определяется только из условия восприятия внутреннего давления по формуле (2.8), определяют по формулам

(2.13)

где µ – коэффициент Пуассона, µ = 0,3.

Полученное расчетное значение толщины стенки трубы округляется до ближайшего большего значения δ_н, предусмотренного государственными стандартами или техническими условиями.

Минимально допустимая толщина стенки трубы при существующей технологии выполнения сварочно-монтажных работ должна быть не менее 1/140 наружного диаметра трубы, но не менее 4 мм. Трубопроводы диаметром до 120 мм на воздействие давления грунта или вакуум не рассчитывают. При расчете толщины стенки трубы запас на коррозию не предусматривается.

· Вычисляется внутренний диаметр нефтепровода

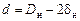(2.14)

где D _н, δ_н –наружный диаметр и номинальная толщина стенки.

· Находятся секундный расход и средняя скорость нефти в трубопроводе

,	(2.15)
.	(2.16)

· Потери напора на трение в трубе определяют по формуле Дарси – Вейсбаха

(2.17)

где λ – коэффициент гидравлического сопротивления; L – длина трубопровода.

Режим движения потока в трубопроводе характеризуется числом Рейнольдса

(2.18)

где ν – расчетная кинематическая вязкость нефти, м²/с.

При ламинарном режиме течения, т.е. при Re < 2320 коэффициент гидравлического сопротивления определяют по формуле Стокса

(2.19)

При турбулентном режиме течения различают три зоны трения: гидравлически гладких труб (λ зависит только от Re), смешанного трения (λ зависит от Re и относительной шероховатости труб ε), квадратичного трения (λ зависит только от ε). Границами этих зон являются переходные числа Рейнольдса, найденные на основании экспериментов:

(2.20)

где – относительная шероховатость труб, выраженная через эквивалентную шероховатость K _э (табл.2.1) и диаметр, мм.

Таблица 2.1

Эквивалентная шероховатость труб (данные А.Д.Альтшуля)

Вид трубы	Состояние трубы	К _э, мм
Бесшовные стальные	Новые чистые
Сварные стальные	После нескольких лет эксплуатации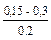
То же	Новые чистые
То же	С незначительной коррозией после очистки
То же	Умеренно заржавленные
То же	Старые заржавленные
То же	Сильно заржавленные или с большими отложениями

________________________

Примечание. В знаменателе указаны средние значения эквивалентной шероховатости.

Условия существования различных зон трения:

− гидравлически гладкие трубы ;

− зона смешанного трения (переходная зона) ;

− зона квадратичного трения .

Для зоны гидравлически гладких труб коэффициент гидравлического сопротивления определяют по формуле Блазиуса

(2.21)

Для зоны смешанного трения коэффициент рекомендуется вычислять по формуле Альтшуля

(2.22)

В зоне квадратичного трения значение коэффициента рекомендуется определять по формуле Шифринсона

(2.23)

Формула (2.17) может быть представлена в обобщенном виде (формула Лейбензона):

(2.24)

где β, m – коэффициенты,

Величины коэффициентов в формуле Лейбензона (2.24):

Режим течения	m	A ₁	β, с²/м
Ламинарный			4,15
Турбулентный:
Зона Блазиуса	0,25	0,3164	0,0246
Зона смешанного трения	0,1	0,206ε^0,15	0,0166ε^0,15
Зона квадратичного трения		λ	0,0827l

Приведенные формулы применимы для расчета труб любого поперечного сечения.

Гидравлический уклон – потеря напора на трение на единицу длины трубопровода:

(2.25)

Если трубопровод имеет вставку другого диаметра d _в, гидравлический уклон в этой вставке определяют через гидравлический уклон и диаметр основной трубы

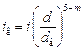(2.26)

Если параллельно с трубопроводом уложен лупинг диаметром d _луп, гидравлический уклон на сдвоенном участке также определяют через гидравлический уклон и диаметр одиночного трубопровода

(2.27)

где ω – расчетный коэффициент,

(2.28)

Когда d _луп = d, то при ламинарном течении (m = 1) ω = 0,5, при турбулентном течении в зоне гидравлически гладких труб (m = 0,25) ω = 0,296 и в зоне квадратичного трения (m = 0) ω = 0,25.

Если к трубопроводу длиной L и диаметром d подключена параллельная нитка длиной X _луп и диаметром d _луп, то потери напора в таком сложном трубопроводе можно определить по формуле

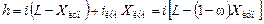(2.29)

Аналогичная зависимость получается и для вставки

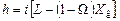где

(2.30)

Если на трубопроводе есть и лупинг и вставка, то потери напора определяются по формуле

(2.31)

На линейной части трубопровода имеются местные сопротивления – задвижки, повороты, сужения и т.п. Потери напора на них определяют по формуле

(2.32)

где ξ_т – коэффициент местного сопротивления, зависящий как от вида сопротивления, так и от характера течения жидкости.

Для магистральных трубопроводов потери напора на местные сопротивления незначительны, их принимают равными до 2 % от потерь на трение.

Кроме того, в конце трубопровода должен поддерживаться остаточный напор H _кп, необходимый для закачки нефти в резервуары.

· В соответствии с Нормами проектирования магистральные нефтепроводы протяженностью более 600 км делятся на эксплуатационные участки длиной от 400 до 600 км. Соответственно их число составляет

где L _г – геометрическая длина трубопровода (включая самотечные участки).

На станциях, расположенных на границе эксплуатационных участков, вместимость резервуарного парка должна составлять 0,3-0,5 суточной пропускной способности трубопровода. Эта емкость должна быть увеличена до 1,0-1,5 Q _сут в случае обеспечения приемно-сдаточных операций [1]. Следовательно, напор H _кп будет использован N _э раз.

Таким образом, полный напор, необходимый для ведения перекачки,

(2.33)

где Δ z – разность геодезических отметок конца z _к и начала z _н трубопровода.

Станции, расположенные на границах эксплуатационных участков, являются головными для своих участков. Поэтому на них устанавливаются подпорные насосы, развивающие суммарный напор N _э h _пн. Следовательно, суммарный напор, развиваемый насосными станциями нефтепровода, складывается из напора, развиваемого всеми подпорными насосами головных насосных станций N _э h _пн и суммарного напора n станций, т.е.

(2.34)

где H _cт – расчетный напор одной станции, м,

(2.35)

· В магистральном трубопроводе устанавливается такой расход Q, при котором суммарный развиваемый напор, определяемый по формуле (2.34), равен полным потерям напора в трубопроводе, вычисляемым по формуле (2.33).

Соответственно, уравнение баланса напоров имеет вид:

(2.36)

Из формулы (2.36) следует, что расчетное число насосных станций

(2.37)

Расчетное число насосных станций, как правило, получается дробным. Оно может быть округлено как в сторону большего (n ′), так и в сторону меньшего (n ′′) числа станций.

Если заказчика устраивает, что фактическая производительность нефтепровода отличается от проектной, то принимается соответствующий вариант. При округлении числа станций в большую сторону требуемая производительность трубопровода достигается при его работе на переменных режимах.

Если же заказчик настаивает на точном обеспечении проектной производительности нефтепровода, то необходимо прибегнуть к регулированию либо характеристик станций, либо трубопровода, либо того и другого.