Лабораторная работа №3.
Исследование пропорционального и интегрального законов регулирования.
1. Цель работы:
· Определить харктер влияния пропорционального и интегрального регуляторов на статтические и динамические свойства объектов регулирования.
· В пакете Simulink создается модель объекта регулирования и определяется её статические и динамические характеристики.
Постановка задачи
Для объекта регулирования, которым является двигатель постоянного тока независимого возбуждения, в m-файле создается математическая модель и исследуются её статические и динамические характеристики.
| R=2;L=0.5;Km=0.1;Kb=0.1;Kf=0.2;J=0.02; | Параметры двигателя |
| W1=tf(0.05,[0.25,1]) | Передаточная функция двигателя, определяющая электромагнитные процессы. |
| W2=tf(5,[0.1,1]) | Передаточная функция двигателя, определяющая электромеханические процессы. |
| t=0:0.1:15; | Задание интервала времени |
| u=1*(t>0&t<15); | Задание управляющего сигнала. |
| Td=-0.1*(t>5&t<10) | Задание возмущения |
| Wust=feedback(W1*W2,0.1) | Передаточная функция замкнутой системы. |
| K=dcgain(Wust) | Коэффициент усиления замкнутой системы. |
| H1=(1/K)*Wust | Передаточная функция замкнутой системы по управлению |
| H2=feedback(W2,(Kb*W1)) | Передаточная функция по возмущению |
| lsim(H1,u,t); | Определение переходного процесса припроизвольных входных сигналах. |
| lsim(H2,u,t); | |
| [yu1,t,x]=lsim(H1,u,t); | Определение векторов выхода по управлению. |
| [yv1,t,x]=lsim(H2,Td,t); | Определение векторов выхода по возмущению. |
| figure(1) | Построение графика переходного процесса разомкнутой системы с использованием принципа суперпозиции. |
| plot(t,(yu1+yv1)), grid on | |
| save proga1 R L Km Kb Kf J W1 W2 t u Td H1 H2 yu1 yv1 | Сохранение результатов выполнения программы. |
Результаты выполнения программы представлены на рис.1 из которого следует, что объект имеет значительную ошибку по возмущению (при приложении нагрузки выходная величина уменьшается в 2 раза).
Рис.1. Характеристики объекта по результатам выполнения программы.
На основании передаточных функций двигателя постоянного тока в пакете Simulink создана модель объекта (рис.2) и проведены её исследования.
Рис.2. Математическая модель объекта в пакете Simulink
На рис.2,А представлена детализированная структурная схема с корректирующим множителем (коэффициент усиления 4.1). На рис.2,Б представлен объект через передаточные функции по управлению и по возмущению, а на рис.2,В представлена структурная схема объекта без учета обратной связи по ЭДС. Результаты испытания объекта в пакете Simulink представлены на рис.3, из которого следует эквивалентность структур на рис.2,А и 2,В и незначительность влияния внутренней обратной связи на статические и динамические характеристики объекта. При изменении корректирующего множителя с 4,1 до 4 и исключении обратной связи по ЭДС переходные процессы трех структурных схем совпадают (рис.3).
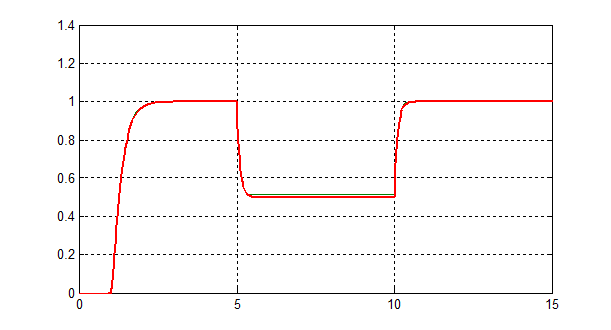
Рис.3. Исследование в пакете Simulink переходных характеристик объекта
Разработаем для объекта, представленного на рис.4,А астатическую систему. Для этого введем регулятор (И-регулятор), усилитель мощности, а затем систему замкнем по выходной величине – угловой скорости (рис.4,Б).
Качество регулирования зависит от коэффициента усиления разомкнутой системы, который, при заданных параметрах системы, определяется коэффициентом усиления регулятора 
. В m–файле приведены два пути определения по логарифмическим характеристикам и методом корневого годографа. Определение по логарифмическим характеристикам – более трудоемкий процесс, т.к. требуется построить семейство ЛАЧХ в функции коэффициента усиления регулятора, а затем путем анализа переходных процессов выбрать нужные параметры регулятора.
Рис.4. Структурная схема исследуемой системы с И – регулятором.
Определение методом корневого годографа более информативно: командами MatLab строиться корневой годограф, а затем на кривой корневого годографа производится щелчок левой кнопкой мыши. В раскрывающемся списке указывается коэффициент усиления, расположение полюсов характеристического уравнения замкнутой системы, коэффициент демпфирования, пере регулирование и частота среза системы. Этими данными исчерпывающе характеризуется переходной процесс, что позволяет выбрать параметры регулятора.
| load proga1 | Загрузка результатаов работы файла proga1.m |
| W3=tf(1,[1,0]) | Передаточная фунция регулятора |
| W4=tf(1,[0.01,1]) | Передаточная фунция усилителя мощности |
| HI=6*H1*W3*W4 | |
| figure(1) | |
| bode(HI), grid on | |
| H1i=feedback(W3*W4*H1,1) | Передаточная фунция усилителя мощности |
| figure(2) | |
| rlocus(W3*W4*H1) | Построение корневого годографа. |
Рис.5. Кривые корневого годографа исследуемой системы
В результате выполнения Программы 2 на рис.5 приведены траектории корней характеристического уравнения замкнутой системы, при изменении коэффициента усиления . При 
на плоскости корней нанесены четыре полосы. На рис.5 представлена ветвь корневого годографа только два правых полюсов, определяющих динамику системы, так как они наиболее близко расположены к мнимой оси. При увеличении полосы из чисто действительных становятся комплексными. Приемлемое значение находится в пределах (
).
Для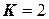 
в m–файле представлена Программа 3 исследования замкнутой системы регулирования.
| load proga1 | Загрузка результатаов работы файла proga1.m |
| W3=tf(2,[1,0]) | Передаточная функция регулятора |
| W4=tf(1,[0.01,1]) | Передаточная функция усилителя мощности |
| H1i=feedback(W3*W4*H1,1) | Передаточная функция замкнутой системы по управлению. |
| lsim(H1i,u,t) | Передаточная функция замкнутой системы по управлению. |
| lsim(H1i,u,t) | Реакция замкнутой системы по управлению на произвольный сигнал |
| [yu2,t,x]=lsim(H1i,u,t) | |
| H2i=feedback(H2,W3*4.1*W1*W4) | Передаточная функция замкнутой системы по возмущению. |
| lsim(H2i,u,t) | Реакция замкнутой системы по возмущению на произвольный сигнал |
| [yv2,t,x]=lsim(H2i,Td,t) | |
| figure(1) | Графики переходных процессов в разомкнутой (yu1+yv1) и замкнутой (yu2+yv2) системах. В замкнутой системе используется И-регулятор |
| plot(t,(yu2+yv2),t,(yu1+yv1)),grid on | |
| save proga3 yu2 yv2 |
Результаты выполнения программы представлены на рис.6 из которого следует, что ввод И-регулятора исключило статическую ошибку (кривая 2), но увеличило пере регулирование.
На рис.7 в пакете Simulink представлена структурная схема систем регулирования, исследуемая в Программе 3. Переходные характеристики систем регулирования, полученные в пакете Simulink, полностью совпадают с соответствующими характеристиками, полученными в программе.
Пропорциональный закон регулирования позволяет добиться небольшого времени регулирования при достаточно небольшой статической ошибки. Расчёт параметров пропорционального регулятора приведена в программе, приведённой ниже.
Рис.6. Переходные характеристики замкнутой системы с И– регулятором
| load proga1 | Загрузка результатаов работы файла proga1.m |
| W3=tf(1,[1,0]) | Передаточная фунция регулятора |
| W4=tf(1) | Передаточная фунция усилителя мощности |
| HI=6*H1*W3*W4 | |
| figure(1) | |
| bode(HI), grid on | |
| H1i=feedback(W3*W4*H1,1) | Передаточная фунция усилителя мощности |
| figure(2) | |
| rlocus(W3*W4*H1) | Построение корневого годографа. |
Рис.7. Структурная схема разомкнутой и замкнутой с И–регулятором систем регулирования.
| load proga1 | Загрузка результатаов работы файла proga1.m и proga3.m |
| load proga3 | |
| W3=tf(2) | Передаточная функция регулятора |
| W4=tf(1,[0.01,1]) | Передаточная функция усилителя мощности |
| H1i=feedback(W3*W4*H1,1) | Передаточная функция замкнутой системы по управлению. |
| lsim(H1i,u,t) | Реакция замкнутой системы по управлению на произвольный сигнал |
| [yu3,t,x]=lsim(H1i,u,t) | |
| H2i=feedback(H2,W3*4.1*W1*W4) | Передаточная функция замкнутой системы по возмущению. |
| lsim(H2i,u,t) | Реакция замкнутой системы по возмущению на произвольный сигнал |
| [yv3,t,x]=lsim(H2i,Td,t) | |
| figure(1) | Графики переходных процессов в разомкнутой (yu1+yv1), замкнутой (yu2+yv2) системе с И-регулятором И (yu3+yv3) c П-регулятором. В замкнутой системе используется И-регулятор |
| plot(t,(yu2+yv2),t,(yu1+yv1),t(yu3+yv3)),grid on | |
| save proga5 yu3 yv3 |
