Модификацией метода простой итерации можно считать метод Зейделя.
В методе простой итерации на 
-ой итерации значения 
, 
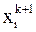вычисляются подстановкой в правую часть (6) вычисленных на предыдущей итерации значений. В методе Зейделя при вычислении 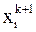используются значения , 
, 
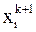, уже найденные на -ой итерации, а не 
, 
, …, 
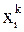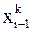, как в методе простой итерации, т.е. -е приближение строится следующим образом:
(9)
Эти формулы являются расчетными формулами метода Зейделя.
Введем нижнюю и верхнюю треугольные матрицы:
и 
.
Матричная запись расчетных формул (9) имеет вид: 
. Так как 
, точное решение 
исходной системы удовлетворяет равенству: 
.
Сходимость метода Зейделя. Достаточным условием сходимости метода Зейделя является выполнение неравенства:
. (10)
Неравенство (10) означает, что для сходимости метода Зейделя достаточно, чтобы любая норма матрицы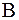 
был меньше единицы.
Если выполнено условие (10), то справедлива следующая оценка погрешности:
, (11)
где 
– норма матрицы .
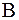Критерий окончания. Если требуется найти решение с точностью 
, итерационный процесс следует закончить, как только на 
-ом шаге выполнится неравенство: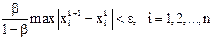 
. Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство 
, где 
. Если выполняется условие
, то можно пользоваться более простым критерием окончания:
.
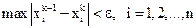Метод Зейделя, как правило, сходится быстрее, чем метод простой итерации. Однако возможны ситуации, когда метод простой итерации сходится, а метод Зейделя сходится медленнее или вообще расходится.
