| Показатели | Номер по заводской спецификации | |||||
| Внутренний диаметр барабана, м | 1,5 | 1,8 | 2,2 | 2,2 | 2,8 | 2,8 |
| Длина барабана, м | ||||||
| Толщина стенок наружного цилиндра, мм | ||||||
| Объём сушильного пространства, м³ | 14,1 | 30,5 | 45,6 | 53,2 | 74,0 | 86,2 |
| Число ячеек, шт | ||||||
| Частота вращения барабана, об/мин | ||||||
| Общая масса, т | 13,6 | 24,7 | 45,7 | |||
| Потребляемая мощность двигателя, кВт | 5,9 | 10,3 | 12,5 | 14,7 | 20,6 | 25,8 |
Действительная скорость воздуха (ω д = 0,6 м/с) отличается от принятой в расчёте (ω = 0,8 м/с) менее чем на 23 %. Некоторое уменьшение интенсивности процесса сушки при снижении скорости газов по сравнению с принятой в расчёте полностью компенсируется избытком объёма выбранной сушилки по сравнению с расчётным. Если расхождение между принятой и действительной скоростями воздуха более существенного, необходимо повторить расчёт, внося соответствующее коррективы.
Определяем среднее время пребывания материала в сушилке.
τ = G м/(G к + W /2). (21)
Количество находящегося в сушилке материала, кг, равно:
G м = V∙β∙ρ м = 45,6∙0,12∙900 =4924,8 кг.
Отсюда
τ = 4924,8/(2,2 + 0,03/2) = 2223 с.
Зная время пребывания, рассчитаем угол наклона барабана.
α ´ = [30∙ L /(d∙n∙τ) + 0,007∙ ω д]∙(180/π); (22)
α´ = [30∙12/(2,2∙5∙2223) + 0,007∙0,6]∙(180/3,14) = 1,08°.
Если полученное значение α ´ мало (меньше 0,5°), число оборотов барабана уменьшают и расчёт повторяют сначала.
Далее необходимо проверить допустимую скорость воздуха, исходя из условия, что частицы высушиваемого материала наименьшего диаметра не должны уноситься потоком сушильного агента из барабана. Скорость уноса, равную скорости свободного витания ω с.в, определяют по уравнению:
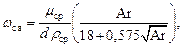 (23)
(23)
где μ ср и ρ ср – вязкость и плотность сушильного агента при средней температуре; d – наименьший диаметр частиц материала, м; Ar ≈ d³∙ρ ч ∙ρ ср ∙g/μ² ср – критерий Архимеда; ρ ч – плотность частиц высушиваемого материала, равная для сахара 1200 кг/м³.
Средняя плотность сушильного агента равна.
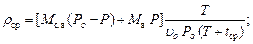 (24)
(24)
 1,46 кг/м³.
1,46 кг/м³.
Критерий Архимеда.
 .
.
Тогда скорость уноса:
 м/с.
м/с.
Рабочая скорость сушильного агента в сушилке (ω д = 0,6 м/с) меньше, чем скорость уноса частиц наименьшего размера ω с.в = 4,1 м/с, поэтому расчёт основных размеров сушильного барабана заканчиваем. В противном случае (при ω д > ω с.в) уменьшают принятую в расчёте скорость сушильного агента и повторяют расчёт.
Расчет профиля барабана
Расчет барабана непрерывного действия, прежде всего, сводится к определению профиля барабана.
Среднюю производительность барабана на каждом участке берем как среднеарифметическую величину между значениями объемной производительности барабана в i сечении Q iср, м3/ч, по формуле:
 , (25)
, (25)
где q i – коэффициент увеличения объема молочного сахара и молочной сыворотки на i сутки; Q с – объемная производительность молочного сахара и молочной сыворотки, м3/ч.
При расчете профиля применен метод численного интегрирования. Всю длину барабана условно разбиваем на несколько участков. В пределах каждого участка физические характеристики молочного сахара и молочной сыворотки будем считать постоянными. Удобно по длине барабан разбить на три участка: начало, середина, окончание.
Расчет средней производительности барабана на участках i -го сечения по сухому сахару Q iср, м3/ч по формуле:
 , (26)
, (26)
где V i – объем рассматриваемого участка м3; φ – коэффициент заполнения, φ = 0,6; t ср – время.
Объем V i рассматриваем как объем усеченного конуса с радиусами R i и R i+1 и длиной l i, по формуле:
 , (27)
, (27)
где l 1= l 2= 5 м.
- при q max= 2,0 радиус барабана равен R i max= 2,2 м;
- при q 1нач=1,4 радиус барабана будет равен отношению q max/ q 1нач = 2,0/1,4 = 1,43, следовательно,
 м;
м;
- при q 2 конеч = 1,85 радиус барабана равен:

Находим объем усеченного конуса с радиусами R i и R i+1 и длиной l i
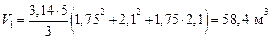

V = V 1 + V 2 = 58,4 + 66,6 = 125 м3.
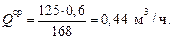
Для расчета барабана непрерывного действия взято уравнение:
 . (28)
. (28)
В частном случае при j = 0,6 и d т = 0,3 D, т. е. r = 0,3 R и после подстановки в него значения безразмерного коэффициента угол наклона свободной поверхности продукта к оси барабана y взят равным нулю потому, что только при этом условии можно достичь максимальной степени наполнения барабана, к чему стремимся, уравнение принимает вид:
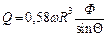 . (29)
. (29)
 В барабане непрерывного действия по мере продвижения продукта от загрузочного конца к разгрузочному его объем будет изменяться. Очевидно, что и объемная производительность Q в различных сечениях барабана должна быть величиной переменной. Чтобы выяснить, за счет каких параметров может осуществляться изменение объемной производительности в разных участках барабана, проведем анализ выражения. Угловая скорость барабана w и угол наклона его Ф являются постоянными во всех сечениях барабана, и за счет этих параметров изменять объемную производительность Q невозможно. Поэтому для определения угловой скорости необходимо принять угол наклона барабана равным Ф = 3º, соответственно угол естественного скоса продукта определяется из графика на рис. 3.
В барабане непрерывного действия по мере продвижения продукта от загрузочного конца к разгрузочному его объем будет изменяться. Очевидно, что и объемная производительность Q в различных сечениях барабана должна быть величиной переменной. Чтобы выяснить, за счет каких параметров может осуществляться изменение объемной производительности в разных участках барабана, проведем анализ выражения. Угловая скорость барабана w и угол наклона его Ф являются постоянными во всех сечениях барабана, и за счет этих параметров изменять объемную производительность Q невозможно. Поэтому для определения угловой скорости необходимо принять угол наклона барабана равным Ф = 3º, соответственно угол естественного скоса продукта определяется из графика на рис. 3.
Для начального сечения зададимся внутренним радиусом барабана R max и углом наклона его Ф. По формуле 6 определим угловую скорость барабана.
 . (30)
. (30)
Для выяснения влияния угла естественного откоса на объемную производительность на рис. 1 показан график, построенный по уравнению:
 . (31)
. (31)
По оси абсцисс отложены значения угла естественного откоса, а по оси ординат – значения безразмерного коэффициента а, которое равно значению а = 0,038. С увеличением угла естественного откоса значения а уменьшаются, следовательно, уменьшается и производительность. По мере продвижения продукта от загрузочного конца барабана к разгрузочному объемная производительность должна увеличиваться, а увеличивающийся угол естественного откоса ее уменьшает.

Необходимая мощность привода вращения барабана расходуется на преодоление силы трения качения бандажей по опорным роликам, силы трения скольжения цапф опорных роликов в подшипниках. Используя проекции сил, действующих на вертикальную ось, составим уравнение
 или
или  , (32)
, (32)
где Р 1 – реакция опорного ролика, Н;  – сила тяжести массы продукта Н;
– сила тяжести массы продукта Н;  – сила тяжести массы барабана, Н; К р = 4 – число опорных роликов; g – ускорение свободного падения, м/с2.
– сила тяжести массы барабана, Н; К р = 4 – число опорных роликов; g – ускорение свободного падения, м/с2.
Р 1 = (565621,05 + 29694,67)/(4∙cos 3) = 148994,3 Н.
Реакция всех опорных роликов Р (Н) рассчитываем по формуле
 , (33)
, (33)
Р = (565621,05 + 29694,67)∙9,81/ cos 3 = 60752,0 Н.
Работа силы трения качения А 1 (Дж) за один оборот барабана определяется как произведение силы трения на длину окружности бандажа:
 , (34)
, (34)
где f тp – коэффициент трения качения, м; D бж – диаметр бандажа барабана, м; R p – радиус опорного ролика, м.
А 1 = 60752,0∙0,0005∙3,14∙2,4/0,36 = 63,58 Дж.
Работа силы трения скольжения цапф опорных роликов в подшипниках за один оборот барабана А 2, Дж, или за D бж/ D p оборотов ролика, по формуле (3.11):
 , (35)
, (35)
где j ск – коэффициент трения скольжения; D ц – диаметр цапф опорного ролика, м; D p – диаметр опорного ролика, м.
А 2 = 60752,0∙0,1∙3,14∙0,16∙2,4/0,72 = 10714 Дж.
Работа силы сопротивления продукта вращению барабана определяется как работа, затрачиваемая на преодоление силы трения скольжения продукта по внутренней поверхности барабана А 3, Дж, по формуле:
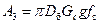 , (36)
, (36)
где f с – коэффициент трения скольжения продукта по поверхности барабана
А 3 = 3,14∙2∙57657,6∙9,81=3552100 Дж.
Полная работа, совершаемая за один оборот барабана А, Дж рассчитываем по формуле:
 , (37)
, (37)
А = 63,58 + 10714 + 3552100 = 3562877 Дж.
Мощность привода, необходимая для вращения барабана N п (кВт), рассчитываем по формуле (14);
 , (38)
, (38)
где п б – частота вращения барабана, c-1; h – КПД передачи привода.
N пр = 3562877×0,017/1000×0,99 = 62 кВт.
Расчет бандажа
Бандажи представляют собой стальные кольца различных профилей, насаживаемые на барабан жестким или свободным креплением. В данном случае применимо жесткое крепление. Бандажи изготовляют из углеродистых сталей марок Ст 5, Ст 6, 40, 45.
Определим максимальный изгибающий момент М, Н×м, находящийся против опор (рис. 4):
 , (39)
, (39)
 где 2 Р 1 – нагрузка на бандаж, Н;
где 2 Р 1 – нагрузка на бандаж, Н;
 , (40)
, (40)
где m – масса вращающихся частей сушилки с продуктом, кг; m = 2257 кг; 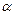 – угол положения ролика бандажа, град,
– угол положения ролика бандажа, град, 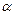 = 300; g – ускорение свободного падения, м/с2, g = 9,81 м/с2;
= 300; g – ускорение свободного падения, м/с2, g = 9,81 м/с2;
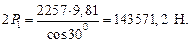
где R б.в – внутренний радиус бандажа, м, R б.в = 0,6, А – коэффициент зависящий от способа крепления бандажа к барабану, А = 0,07;

Момент сопротивления для сечения бандажа W, м3, определяем по формуле:
 , (41)
, (41)
где Д – внутренний диаметр бандажа, м, Д = 2,2 м; S – площадь поперечного сечения бандажа, м2;
 , (42)
, (42)
где a – ширина бандажа, м, a = 0,04 м; b – высота бандажа, м, b = 2 м;
 ,
,
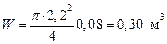 .
.
Максимальное напряжение изгиба,  , Н/м2, определяем по формуле:
, Н/м2, определяем по формуле:
 , (43)
, (43)
где М – момент изгибающий бандаж, Н×м, М = 10049,9 Н×м; W – момент сопротивления сечения бандажа, м3, W = 0,025 м3;
 .
.
Напряжение  не превышает допускаемого напряжения [
не превышает допускаемого напряжения [  ]=100 кН/м2.
]=100 кН/м2.






