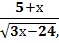Как указать область определения выражения или функции, содержащей

Арифметический квадратный корень.

1.Определение: 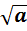= b, если b ≥ 0 и b ²= a. Пример: 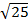=5,т.к 5>0, 5²=25.

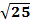= - 5 не имеет смысла.- 5<0.

2.( 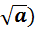² = a. Пример: ( 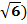² = 6 .

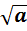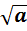∙ = a. Пример: 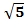∙ 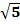= 5.

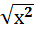=│х

3.Свойства: 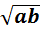<=> 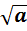∙ 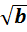, если a ≥ 0, b ≥0.

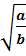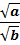<=> , если a ≥ 0, b > 0.

4.Число 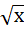рациональное, если корень из этого числа извлекается.

Число 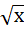иррациональное, если корень из этого числа не извлекается

5. Как сравнить числа, расположить в порядке возрастания или убывания?

1) Внести числа под корень.

2) Сравнить подкоренные числа.

3)Сравнить первоначальные числа, используя пункт 2.(расположить в порядке возрастания

или убывания первоначальные числа используя пункт 2.)

Как указать область определения выражения или функции, содержащей

?

Выражение имеет смысл, если подкоренное выражение ≥ 0.

Если находится в знаменателе, то подкоренное выражение строго > 0.

1)Решить неравенство.

2)Записать ответ в виде неравенства или промежутка.

7. График функции у = 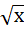. Ветвь параболы.

 

 

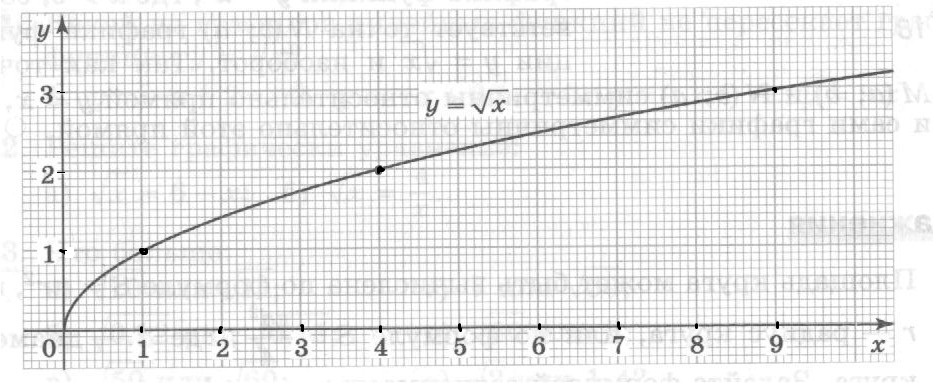
Задание –Владение понятием квадратного корня.

1.Выделите те из чисел, которые являются рациональными:

0, 1, , , , , , , - .

 

 

 

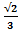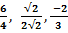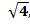
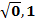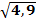
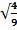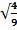2.

3.

4.

5.

Задание – Найти область определения.

1. ,

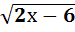2.

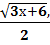
3. у =