Алгоритм Фибоначчи
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции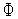 
(
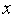), определенной в замкнутой области допустимых значений 
=[ 
, 
],
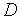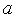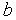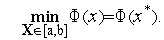
Числа Фибоначчи и их некоторые свойства.
Числа Фибоначчи задаются следующим рекуррентным уравнением:
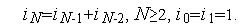
| (1) |
Числа Фибоначчи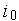 
,..., 
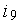приведены в нижеследующей табл. 1.
Таблица 1
| ... | ||||||||||
| ... |
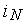
Общее выражение для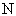 
-го числа Фибоначчи можно получить из решения уравнения (1):
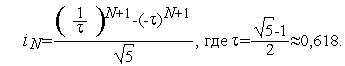
При больших значениях членом (- 
) N +1 можно пренебречь. При этом
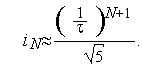
| (2) |
Отсюда следует, что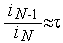 
. Т.е. отношение двух соседних чисел Фибоначчи примерно постоянно и равно .
Алгоритм Фибоначчи.
Алгоритм Фибоначчи относится к классу поисковых методов оптимизации и включает в себя два этапа.
Первый этап состоит из ( -1)-й итерации для 
=1,2,… -1. Рассмотрим схему -й итерации, когда ТИН r =[ 
, 
]:
1. Вычисляем величины
2. Вычисляем значения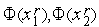 
функции 
().
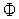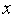3. Если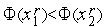 
, то выполняем присваивания 
, 
, 
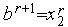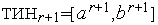. Иначе - выполняем присваивания 
, 
, 
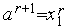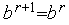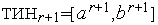
Алгоритм Фибоначчи обладает тем свойством, что после выполнения ( -1)-й итерации имеет место следующая ситуация: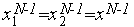 
. Т.е. в результате ( -1)-й итерации сужение текущего интервала неопределенности не происходит:
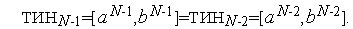
Второй этап призван решить по какую сторону от точки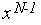 
лежит точка минимума функции ().
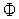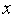Второй этап выполняется по следующей схеме:
1. Находим точку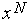 
= + 
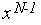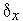, где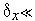 
|ТИН N -1| - свободный параметр алгоритма.
2. Вычисляем значение функции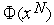 
.
3. Если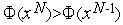 
, то выполняем присваивания 
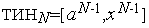. Иначе - выполняем присваивания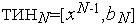 
В качестве приближенного значения точки минимума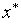 
с равными основаниями может быть принята любая точка ТИН N.
