Задачи, связанные с оцениванием экологического риска и разработкой мер по его снижению, требуют собственного математического подхода, для чего может быть использован аппарат теории принятия решений. Ниже рассматриваются его основы в предельно упрощенном виде [27].
В настоящее время для анализа и решения проблем, вовлекаемых в процесс принятия связанных с риском решений, широко используется так называемый метод деревьев. К числу его достоинств относятся удобство и наглядность графического представления, а также существенное облегчение расчетов на компьютерах. Метод деревьев особенно эффективен в тех случаях, когда сложная проблема может быть расчленена на то или иное количество сравнительно простых задач, каждая из которых решается отдельно, а затем производится своеобразный синтез сложного решения. Подобно обычному, дерево решений содержит различные части — ствол и разные по величине ветви, причем все они формируют единый организм. Поведением этого организма и отдельных его частей в случае обыкновенного дерева управляют законы биологии, а в случае дерева решений — законы теории вероятностей. Последние обеспечивают когерент-ность (согласованность) системы, которой является рассматриваемое дерево.
2.2.1. Построение дерева решений
Рассмотрим пример построения дерева для решения так называемой задачи инвестиций, заключающейся в следующем. Некий бизнесмен имеет в своем распоряжении 5000 долларов и стоит перед дилеммой: оставить эти деньги в банке или закупить на них товар, который затем предполагается выгодно продать. Однако, эта операция связана с риском, так как цена данного товара на рынке может или повыситься, или, наоборот, понизиться. Бизнесмен готов пойти на риск потери, оцениваемой в 1000 долларов, и в то же время он предполагает получить в результате операции прибыль, которая составит, по его оценке, также 1000 долларов. Пусть вероятность повышения цены товара на рынке в полтора раза больше вероятности понижения этой цены, тогда первому событию (повышение цены) надо приписать вероятность 0,6, а второму событию (понижение цены) — вероятность, равную 0,4.
Сформулированные условия можно представить в виде простой таблицы (табл. 2.1) со следующими обозначениями: а 1 и а 2 — рассматриваемые события (повышение и понижение цены товара соответственно); d 1 и d 2 — возможные решения, т.е. соответственно инвестировать и оставить деньги в банке; p (аi) — вероятность события а 1 (i =1) или а 2 (i =2).
Таблица 2.1. Возможные последствия решений, выраженные
в долларах, и вероятности событий а 1 и а 2
| События | а 1: цена повысится | а 2: цена понизится |
| d 1: инвестировать | ||
| d 2: оставить в банке | ||
| р (аi) | 0,6 | 0,4 |
Предположим теперь, что бизнесмен прибегает к услугам брокера, который за плату в t долларов консультирует его по инвестированию средств в рассматриваемую операцию с товаром. Очевидно, что возможны два совета брокера: покупать товар (обозначим этот вариант x 1) или не покупать (вариант x 2). Пусть надежность советов брокера оценивается вероятностями:
p (x 1/ a 1) = 0,70 — вероятность правильного совета (покупать) в случае повышения цены товара;
p (x 2/ a 2) = 0,65 — вероятность правильного совета (не покупать) в случае понижения цены товара.
Видно, что эти вероятности являются по своей структуре условными. Ими могут выступать субъективные оценки данного бизнесмена или же сведения, полученные им от третьих лиц. Приведенные конкретные значения этих вероятностей говорят о том, что бизнесмен считает брокера более способным к выигрышу (прибыли), нежели к потере (к потерям надо относить и неполученную прибыль). Действительно, шансы брокера на выигрыш составляют 70%, а на проигрыш — 65%.
Таким образом, инвестор должен решить, во-первых, покупать ли ему консультацию (совет) брокера, и во-вторых, покупать ли товар (как с консультацией брокера, так и без нее). Дерево решений для этой проблемы изображено на рис. 2.1. Представляемое дерево “растет” не вертикально, а горизонтально, при этом будем считать, что ствол расположен слева, а все ветви направлены вправо.
Рассмотрение начнем с левого края рисунка, т.е. от ствола дерева. Начальная стадия состоит в том, что бизнесмен должен выполнить одно из трех действий, изображенных тремя ветвями. Первая ветвь имеет обозначение “брокер” и соответствует обращению к брокеру и оплату его консультации. Вторая ветвь (d 1) означает решение инвестировать без совета брокера, а третья (d 2) — решение оставить деньги в банке.
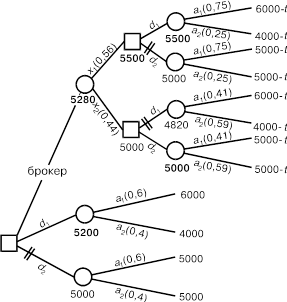
Рис. 2.1. Дерево решений в задаче об инвестициях
На рис. 2.1 имеются четырехзначные суммы в долларах, которые будут объяснены ниже, а пока будем следовать по ветви с маркировкой “брокер”. Поскольку обращение за консультацией состоялось, то возможны два варианта совета: покупать или не покупать товар. В соответствии с этим ветвь расщепляется на две, одна их них имеет маркировку x 1 (“покупать”), другая — x 2 (“не покупать”). Какой бы из этих двух ветвей ни следовать, каждый раз нужно будет выбирать между действиями d 1 (“инвес-тировать”) и d 2 (“оставить деньги в банке”). Отсюда — дальнейшее разветвление, причем каждая из новых ветвей, в свою очередь, дает еще по два отвода, в соответствии с повышением (a 1) или понижением (a 2) цены товара. Аналогичным образом прослеживается часть дерева с ветвями d 1 и d 2, “растущими” из начальной точки — каждая из них расщепляется на две, что означает учет как повышения, так и понижения цены товара.
Следовательно, мы получили дерево, составленное из нескольких ветвей, и каждая ветвь отображает собой или принятое решение или полученный результат. Подчеркнем, что при построении дерева (слева направо) соблюдался нормальный порядок следования рассматриваемых событий — от прошлого к будущему.
Рассмотрим теперь подробнее те точки, в которых происходит расщепление ветвей, они называются узлами. Существуют узлы двух принципиально различных типов, будем называть их узлами решений и узлами случаев. Обратимся снова к узлу в левой части рис. 2.1, здесь находится первый узел, дающий три ветви (“брокер”, d 1 и d 2). Выбор одной из этих ветвей зависит от лица, которое принимает решение после рассмотрения всех трех возможностей. По этой причине данный узел и называют узлом решения, обозначая квадратиком. Если следовать по любой из трех отходящих от этого узла ветвей, например, по ветви “брокер”, то на пути встретится узел с ветвями x 1 и x 2. Лицо, принимающее решение, не держит под контролем ситуацию, отображаемую этим узлом (здесь решение принимает брокер), следовательно, оно не может выбрать ту или иную ветвь. Правда, это лицо способно приписать разветвлениям от данного узла некоторые вероятности. Именно поэтому рассматриваемый узел логично назвать узлом случаев, такие узлы будем обозначать кружками.
Ветви x 1 и x 2 приводят к узлам решений, поскольку при подходе к ним бизнесмену надлежит решить: инвестировать деньги или же оставить их в банке. А каждая из ветвей, обозначенная на рассматриваемом дереве, как d 1 или d 2, должна заканчиваться узлом случаев, так как бизнесмен не может знать заранее, как поведет себя цена товара на рынке.






