For one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, could be obtained by means of Newton's second law and Hooke's law.

where m is the inertial mass of the oscillating body, x is its displacement from the equilibrium (or mean) position, and k is the spring constant.
Solving the differential equation above, a solution which is a sinusoidal function is obtained.

In the solution, c 1 and c 2 are two constants determined by the initial conditions, and the origin is set to be the equilibrium position. Each of these constants carries a physical meaning of the motion: A is the amplitude (maximum displacement from the equilibrium position), ω = 2π f is the angular frequency, and φ is the phase.

Position, velocity and acceleration of a harmonic oscillator
Using the techniques of differential calculus, the velocity and acceleration as a function of time can be found:


Position, velocity and acceleration of a SHM as phasors
Acceleration can also be expressed as a function of displacement:
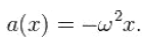
Then since ω = 2π f,
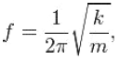
and since T = 1/ f where T is the time period,

These equations demonstrate that the simple harmonic motion is isochronous (the period and frequency are independent of the amplitude and the initial phase of the motion).






