The displacement of a moving object is directly proportional to both velocity and time. Acceleration compounds this simple situation. Now the velocity is also directly proportional to time. Try saying this in words and it sounds ridiculous. “Displacement is directly proportional to time and directly proportional to velocity, which is directly proportional to time.” Time is a factor twice, making displacement proportional to the square of time. A car accelerating for two seconds would cover four times the distance of a car accelerating for only one second (22 = 4). A car accelerating for three seconds would cover nine times the distance (32 = 9).
Would that it should be so simple. This example only works when initial velocity is zero. Change in displacement is proportional to the square of time when acceleration is constant and initial velocity is zero. A true general statement would have to take into account any initial velocity and how the velocity was changing. This results in a terribly messy proportionality statement. Change in displacement is directly proportional to time and proportional to the square of time when acceleration is constant. A function that is both linear and square is said to be quadratic, which allows us to compact the previous statement considerably. Change in displacement is a quadratic function of time when acceleration is constant
Proportionality statements are useful, but not as concise as equations. We still don’t know what the constants of proportionality are for this problem. The only way to answer that is through algebra. Start with the definition of velocity, expand Δ x, and solve it for displacement.



 [a]
[a]
To continue, we need to resort to a little trick first published in the Fourteenth Century at Merton College, Oxford (and sometimes called the Merton Rule). When acceleration is constant, the velocity will change uniformly from its initial value to its final value and the average will lie halfway between the extremes. Thus, the average velocity is just the arithmetic mean of the initial and final velocities. Average velocity is the average of the final and initial velocities when acceleration is constant.
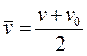
Substitute the first equation of motion [1] into this equation (4) and simplify with the intent of eliminating v.

[b]
Finally, substitute [b] into [a] and solve for x as a function of t.


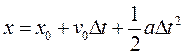
[2]
Since velocity is also the first derivative of displacement with respect to time, this equation can also be derived using calculus. In fact, it’s much easier than using algebra. Just reverse the action of the definition. Instead of differentiating displacement to find velocity, integrate velocity [1] to find displacement.



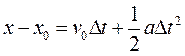
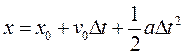
[a]
The symbol x 0 (ex nought) is the initial displacement. Many times, this value is zero and if it isn’t, we can make it so. If you ask me, “ When should we do this? ” I would say, “ It depends on the problem,” and leave it to you to decide. There is no rule that you can memorize is this case. You have to understand what the equation says and then learn how to apply it to a particular situation. Similarly x is often called the final displacement, but this does not make it the “last displacement”, rather it is the displacement at the end of the time interval during which the acceleration was constant.
Something else to notice is the similarity between equations [2] and [a]. When acceleration is zero, our second equation of motion reverts to a rearranged constant velocity equation. As predicted, displacement is in part directly proportional to time and in part directly proportional to time squared.
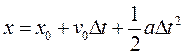
[2]
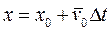 [a]
[a]
Although the velocity symbols in the two equations may look different, they do indeed represent the same quantity. If there is no acceleration, then the velocity is constant, which means that the initial velocity is the same as the final velocity is the same as the average velocity. The acceleration term at the end is an adjustment to the constant velocity equation to account for the the fact that the velocity is changing. A positive acceleration would increase the displacement and a negative acceleration would decrease it. This is exactly what one would expect. If an object’s velocity was increasing, it would move farther than if it had stayed at a constant velocity. Likewise, if an object’s velocity was decreasing, it would have a smaller displacement than if its velocity were constant. It’s good to see that the equations behave in a realistic manner. Otherwise all this math would be a waste of time.






