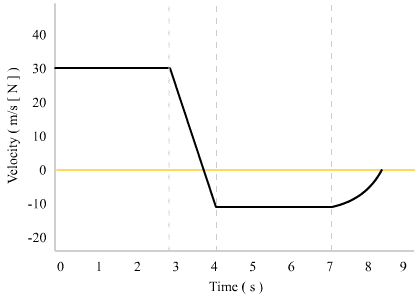
Analysis:
1. Our data is captured when the object is already moving, it has a constant velocity of 30m/s [N] up to the 3rd second of observation.
2. The object decelerates, reaches 0 velocity and then begins travelling in the south direction.
3. The object travels at a constant velocity south for 3 seconds.
4. The object smoothly decelerates and comes to a stop.
We can deduct interesting information from a velocity-time graph:The slope of the line is the acceleration, but the area under the the line is the displacement!
Let’s see how to determine the displacement an object undergoes during a given time:
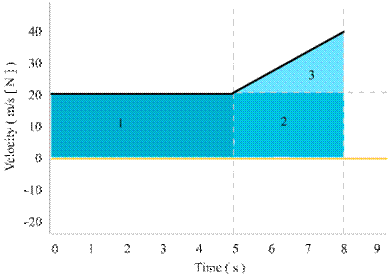
Determining the displacement of the object in the first 5 (area 1) seconds is simple, the shape is a square and you multiply 20m/s times 5 seconds.
The displacement during those 5 seconds is 100m [N]. The displacement undergone by the object from 5 seconds to 8 seconds is a bit harder to determine, because the shape under the line is more complex. The area of the square (area 2) is 20m/s times 3 seconds, and represents a displacement of 60m [N]. The area of the triangle (area 3) is 20m/s (40 – 20) times 3 seconds, divided by two. Thus the area of the triangle ends up reperesenting a displacement of 30m [N].
We can deduct that during the 8 seconds of the object’s motion it has undergone a displacement of 100 + 60 + 30 metres northward.
When the line falls blow the 0m/s mark the displacement is happening in the opposite direction. This “negative displacement” should be subtracted from the “positive displacement” to find out what is the resultant displacement and its direction.