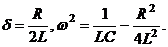Линейным неоднородным уравнением n -го порядка спостоянными коэффициентами называется уравнение вида
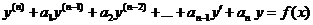 ,
,
где а 1, а 2,..., а n — некоторые действительные числа.
Это частный случай уравнения (7), когда выполняется условие:
а i (х) = а i = cons t (i = 1, 2,..., n).
Общее решение линейного неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения:
у = у 0 + у*,
где у 0 — общее решение соответствующего линейного однородного уравнения
у * — частное решение данного линейного неоднородного уравнения.
Частное решение у* данного линейного неоднородного уравнения можно найти методом подбора (методом неопределённых коэффициентов). Этот метод применим только в том случае, если правая часть уравнения неоднородного уравнения имеет вид
f (x) = е a x × (Pn (x)cos b x + Qm (x)sin b x), где Pn (x), Qm (x) — многочлены от х степени n и m соответственно; a, b — постоянные.
Тогда частное решение у* уравнения существует в виде
у* = х s × е a x × (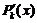 cos b x +
cos b x + 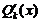 sin b x), (16)
sin b x), (16)
где s — кратность корня a ± b i характеристического уравнения (если a ± b i не является корнемхарактеристического уравнения, то s = 0); k = max (n, m); 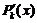 ,
, 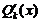 — многочлены от х степени k общего вида с неопределёнными коэффициентами.
— многочлены от х степени k общего вида с неопределёнными коэффициентами.
Простейшие виды правых частей f (x)уравнения и соответствующие им частные решения у*, указаны в табл. 2.
Таблица 2. Частные решения линейного неоднородного
уравнения n -го порядка с постоянными коэффициентами
| № | Правая часть f (x) уравнения (14) | Вид частного решения у* уравнения (14) | |
| l не является корнем характеристического уравнения (12) | l является корнем характеристического уравнения (12) | ||
| 1 | f (x) = Pn (x) – многочлен степени n | l = 0 – не корень Þ у* = Qn (x) – многочлен степени n | l = 0 – корень (12) кратности s Þ Þ у* = х s × Qn (x) – многочлен степени s + n |
| 2 | f (x) = е a x ×Pn (x) | l = a – не корень Þ Þ у* = е a x ×Qn (x) | l = a – корень кратности s Þ Þ у* = е a x × х s × Qn (x) |
| 3 | f (x) = Pn (x) × cosb x + + Qm (x)sinb x | l = ± b i – не корень Þ Þ у * = P'k (x) cos b x + Q'k (x) sin b x | l = ± b i – корень кратности s Þ Þ у * = х s × (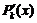 cos b x + Q'k (x) sin b x) cos b x + Q'k (x) sin b x)
|
| 4 | f (x) = е a x × (Pn (x) ×× cosb x + Qm (x) sinb x) | l = a ± b i – не корень Þ Þ у * = е a x × (P'k (x) cos b x + + Q'k (x) sin b x) | l = a ± b i – корень кратности s Þ Þ у * =х s ×е a x (P'k (x) cos b x + + Q'k (x) sin b x) |
Пример 1. Найти общее решение уравнения
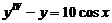 .
.
Решение. Данное уравнение является линейным неоднородным уравнением четвёртого порядка спостоянными коэффициентами. Его общее решение найдём по формуле (10):
у = у 0 + у*,
где у 0 — общее решение соответствующего линейного однородного уравнения 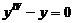 ; у* — частное решение данного линейного неоднородного уравнения.
; у* — частное решение данного линейного неоднородного уравнения.
1. Найдём общее решение у 0 соответствующего линейного однородного уравнения
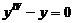 .
.
Запишем для него характеристическое уравнение
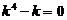 .
.
Его корни: k 1,2 = ± 1 — простые действительные числа (п. 2.3, случай 1); k 3,4 = ± i — комплексные сопряжённые простые корни (п. 2.3, случай 3; a = 0, b = 1). Следовательно, общее решение однородного уравнения имеет вид
у 0 = С 1 е x + C 2 е –х + С 3cos x + C 4sin x.
2. Найдём частное решение у* данного линейного неоднородного уравнения методом неопределённых коэффициентов.
Правая часть уравнения
f (x) = 10 cos x
является частным случаем выражения (15); в табл. 2 это случай 3, где Pn (x)= P 0(x)=10,
b =1, Qn (x) = Q 0(x) = 0.
Так как ± i — однократные корни характеристического уравнения, то по табл. 2 (последний столбец третьей строки) получаем частное решение у* данного линейного неоднородного уравнения:
у* = х × (А 1cos x + А 2sin x).
Найдём неизвестные величины А 1, А 2. Для этого продифференцируем четыре раза получившееся уравнение:
у*' = (х × (А 1 cos x + А 2sin x))' = А 1 cos x + А 2sin x + х × (– А 1sin x + А 2 cos x);
у*'' = 2 А 2cos x – 2 А 1sin x – х × (А 1 cos x + А 2sin x);
у*''' = – 3 А 1cos x – 3 А 2sin x – х × (– А 1 sin x + А 2cos x);
у* IV = 4 А 1sin x – 4 А 2 cos x + х × (А 1cos x + А 2sin x).
Подставим выражения для у IV и у в исходное уравнение у IV ‑ y = 10 cos x:
4 А 1sin x – 4 А 2cos x + x (А 1cos x + А 2sin x) – хА 1cos x – хА 2sin x = 10 cos x.
После преобразований получим уравнение:
4 А 1sin x – 4 А 2cos x = 10 cos x.
Приравняем коэффициенты в левой и правой частях при sin x и cos x:
4 А 1 = 0; – 4 А 2 = 10.
Отсюда А 1 = 0; А 2 = – 5/2. Подставим эти значения в частное решение у* данного линейного неоднородного уравнения:
у* = х × (А 1cos x + А 2sin x) = – 5/2 х sin x.
3. Таким образом, общее решение данного линейного неоднородного уравнения спостоянными коэффициентами имеет вид
у = у 0 + у* = С 1 е x + C 2 е -х + С3cos x + C 4sin x ‑ 5/2 х sin x.
Пример 2. Найти общее решение уравнения
у'' ‑ 3 у' + 2 y = x 2 + 3 x.
Решение. Данное уравнение является линейным неоднородным уравнением второго порядка спостоянными коэффициентами. Его общее решение найдём по формуле (10):
у = у 0 + у*,
где у 0 — общее решение соответствующего линейного однородного уравнения у'' – 3 у' + 2 y = 0;
у* — частное решение данного линейного неоднородного уравнения.
1. Найдём общее решение у 0 соответствующего линейного однородного уравнения
у'' ‑ 3 у' + 2 y = 0.
Запишем для него характеристическое уравнение
k 2‑ 3 k + 2 = 0.
Его корни k 1= 1, k 2= 2 — простые действительные числа (п. 2.3, случай 1). Следовательно, общее решение однородного уравнения имеет вид
у 0 = С 1 е x + C 2 е 2х.
2. Найдём частное решение у* данного линейного неоднородного уравнения методом неопределённых коэффициентов.
Правая часть уравнения f (x) = x 2 + 3 x — многочлен 2-й степени — является частным случаем выражения (15). В табл. 2 это случай 1, где Pn (x)= P 2(x)= x 2 + 3 x. Так как 0 не является корнем характеристического уравнения, то по табл. 2 (предпоследний столбец первой строки) получаем частное решение у* данного линейного неоднородного уравнения:
у* = Q 2(x) = А 1 x 2 + А 2 x + А 3.
Найдём неизвестные величины А 1, А 2, А 3. Для этого продифференцируем два раза получившееся уравнение:
у*' = (А 1 x 2 + А 2 x + А 3 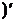 = 2 А 1 x + А 2; у*'' = 2 А 1.
= 2 А 1 x + А 2; у*'' = 2 А 1.
Подставим выражения для у'', у' и у в исходное уравнение:
2 А 1 – 6 А 1 x – 3 А 2 + 2 А 1 x 2+ 2 А 2 x + 2 А 3= x 2+ 3 x.
После преобразований получим уравнение:
2 А 1 x 2+ (2 А 2– 6 А 1) x + (2 А 1 – 3 А 2 + 2 А 3) = x 2+ 3 x.
Приравняем коэффициенты в левой и правой частях полученного равенства при одинаковых степенях неизвестного x:
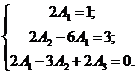
Решив систему, получим А 1 = 1/2; А 2 = 3; А 3 = 4. Подставим эти значения в частное решение у* данного линейного неоднородного уравнения:
у* = 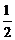 x 2 + 3 x + 4.
x 2 + 3 x + 4.
3. Таким образом, общее решение данного линейного неоднородного уравнения с постоянными коэффициентами имеет вид
у = у 0 + у* = С 1 е x + C 2 е 2х + 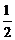 x 2 + 3 x + 4.
x 2 + 3 x + 4.
Пример 3. Найти общее решение уравнения
у'' ‑ 2 у' + y = x ∙ ex.
Решение. Данное уравнение является линейным неоднородным уравнением второго порядка спостоянными коэффициентами. Его общее решение найдём по формуле (10):
у = у 0 + у*,
где у 0 — общее решение соответствующего линейного однородного уравнения у'' ‑ 2 у' + y = 0;
у* — частное решение данного линейного неоднородного уравнения.
1. Найдём общее решение у 0 соответствующего линейного однородного уравнения
у'' ‑ 2 у' + y = 0.
Запишем для него характеристическое уравнение
k 2– 2 k + 1 = (k – 1)2 = 0.
k 1 = k 2= 1 — действительный корень кратности 2 (п. 2.3, случай 2). Следовательно, общее решение однородного уравнения имеет вид
у 0 = е x (С 1+ C 2 х).
2. Найдём частное решение у* данного линейного неоднородного уравнения методом неопределённых коэффициентов.
Правая часть уравнения f (x) = x ∙ е x является частным случаем выражения (15). В табл. 2 это случай 2, где Pn (x)= P 1(x)= х, a = 1. Так как a = 1 — это корень характеристического уравнения кратности 2, то по табл. 2 (последний столбец второй строки) получаем частное решение у* данного линейного неоднородного уравнения:
у* = е x × х 2 × Q 1(x) = е x × х 2 × (А 1 x + А 2) = е x × (А 1 х 3+ А 2 х 2).
Найдём неизвестные величины А 1, А 2. Для этого продифференцируем два раза получившееся уравнение:
у*' = (е x × (А 1 х 3+ А 2 х 2) 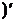 = е x × (А 1 х 3+ (А 2+ 3 А 1) х 2+ 2 А 2 x);
= е x × (А 1 х 3+ (А 2+ 3 А 1) х 2+ 2 А 2 x);
у*'' = е x × (А 1 х 3+ (А 2+ 3 А 1) х 2+ 2 А 2 x + 3 А 1 х 2+ 2(А 2+ 3 А 1) х + 2 А 2).
Подставим выражения для у'', у' и у в исходное уравнение:
е x × (А 1 х 3+ (А 2+ 3 А 1) х 2+ 2 А 2 x + 3 А 1 х 2+ 2(А 2+ 3 А 1) х + 2 А 2) – 2 е x × (А 1 х 3+ (А 2+ 3 А 1) х 2+ 2 А 2 x +
+ е x × (А 1 х 3+ А 2 х 2) = х ∙ е х.
Разделим равенство на е x и после несложных преобразований получим уравнение
6 А 1 x + 2 А 2= x.
Приравняем коэффициенты в левой и правой частях полученного равенства при одинаковых степенях неизвестного x: 6А 1 = 1; 2 А 2 = 0. Откуда получим А 1 = 1/6; А 2 = 0. Подставим эти значения в частное решение у* данного линейного неоднородного уравнения:
у* = 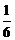 е x × х 3.
е x × х 3.
3. Таким образом, общее решение данного линейного неоднородного уравнения спостоянными коэффициентами имеет вид
у = у 0 + у* = е x (С 1+ C 2 х) + 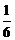 е x × х 3 = е x (С 1+ C 2 х +
е x × х 3 = е x (С 1+ C 2 х + 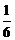 х 3).
х 3).
Пример 4. К источнику с электродвижущей силой (ЭДС), равной е (t), подключили контур, состоящий из последовательно соединённых катушки индуктивности L, омического сопротивления R и ёмкости C. Найти силу тока i в цепи как функцию времени t, если в начальный момент времени сила тока в контуре и заряд конденсатора равны нулю.
Решение. По закону Кирхгофа электродвижущая сила в цепи равна сумме падений напряжения на индуктивности, сопротивлении и ёмкости:
е (t) = UL + UR + UC,
где UL = 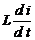 ; UR = R i; UC =
; UR = R i; UC = 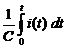 .
.
Заметим, что последнее равенство получается из соотношения между силой тока и зарядом конденсатора: 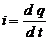 , откуда
, откуда 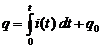 , а так как UC =
, а так как UC = 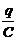 , то UC =
, то UC = 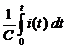 +
+ 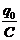 . По условию задачи q 0= 0. Таким образом, получаем интегрально-дифференциальное уравнение е (t) =
. По условию задачи q 0= 0. Таким образом, получаем интегрально-дифференциальное уравнение е (t) = 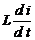 + R i +
+ R i + 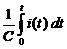 . Продифференцировав его по t, получим линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:
. Продифференцировав его по t, получим линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:
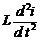 + R
+ R 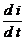 +
+ 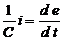 .
.
Здесь возможны два случая: 1) е (t) = С = сonst; 2) е (t) = E sin w t.
Рассмотрим первый случай. Здесь 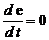 . Тогда получим однородное уравнение второго порядка с постоянными коэффициентами:
. Тогда получим однородное уравнение второго порядка с постоянными коэффициентами:
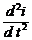 +
+ 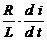 +
+ 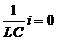 .
.
Характеристическое уравнение 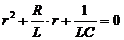 имеет корни
имеет корни
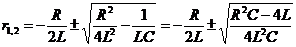 .
.
Если 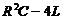 ³ 0, то корни характеристического уравнения — действительные и общее решение есть функция непериодическая. Соответственно апериодической является и сила тока. Никаких электрических колебаний в цепи не произойдёт.
³ 0, то корни характеристического уравнения — действительные и общее решение есть функция непериодическая. Соответственно апериодической является и сила тока. Никаких электрических колебаний в цепи не произойдёт.
Если же 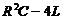 < 0, то общее решение
< 0, то общее решение
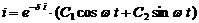 ,
,
где  ,
, 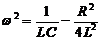 определяет электрические колебания.
определяет электрические колебания.
Так как 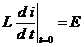 , то
, то 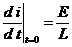 .
.
Следовательно, начальные условия можно записать в виде
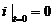 ;
; 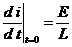 .
.
Дифференцируя i по t, имеем
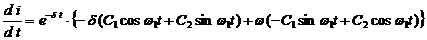 .
.
Подставив t = 0 в выражения для i и 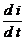 , получим
, получим
0 = С1, 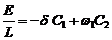 ,
,
откуда С 1 = 0, 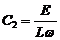 .
.
Итак, частное решение уравнения принимает вид
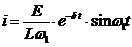 .
.
Рассмотрим второй случай. Так как е (t) = E sin w t, то 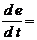 E × w × cos w t. Тогда получим линейное неоднородное уравнение второго порядка с постоянными коэффициентами
E × w × cos w t. Тогда получим линейное неоднородное уравнение второго порядка с постоянными коэффициентами
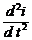 +
+ 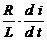 +
+ 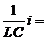 E × w × cos w t.
E × w × cos w t.
Его общее решение найдём по формуле (10):
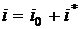 ,
,
где i 0 - общее решение соответствующего линейного однородного уравнения (его мы уже нашли, рассматривая первый случай); 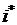 - частное решение данного линейного неоднородного уравнения. Найдём частное решение
- частное решение данного линейного неоднородного уравнения. Найдём частное решение 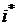 данного линейного неоднородного уравнения методом неопределённых коэффициентов.
данного линейного неоднородного уравнения методом неопределённых коэффициентов.
Правая часть уравнения f (t) = E × w × cos w t является частным случаем выражения (15);
в табл. 2 это случай 3, где Pn (t)= P 0 (t) == E × w × cos w t, b =w, Qn (t) = Q 0 (t) = 0. Так как ± w i не является корнем характеристического уравнения, то по табл. 2 (предпослед-ний столбец третей строки) получаем частное решение 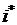 линейного неоднородного уравнения:
линейного неоднородного уравнения:
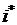 = А1 cos w t + А2 sin w t.
= А1 cos w t + А2 sin w t.
Найдём неизвестные величины А1, А2. Для этого продифференцируем два раза получившееся уравнение:
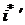 = (А1 cos w t + А2 sin w t
= (А1 cos w t + А2 sin w t  = - А1 wsin w t + А2 wcos w t;
= - А1 wsin w t + А2 wcos w t;
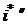 = - А1 w2cos w t 0 - А2 w2sin w t.
= - А1 w2cos w t 0 - А2 w2sin w t.
Подставим выражения для 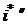 ,
, 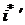 и i в исходное уравнение:
и i в исходное уравнение:
- А1 w2cos w t - А2 w2sin w t + 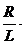 (- А1 wsin w t + А2 wcos w t) +
(- А1 wsin w t + А2 wcos w t) + 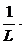 (А1 cos w t + А2 sin w t) =
(А1 cos w t + А2 sin w t) =
= E × w × cos w t.
После преобразований, приравнивая коэффициенты в левой и правой частях при sin w t и cos w t, получим:
А1 = 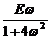 ; А2 =
; А2 =  .
.
Подставим эти значения в частное решение 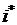 данного линейного неоднородного уравнения, получим:
данного линейного неоднородного уравнения, получим:
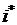 =
= 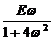 cos w t +
cos w t + 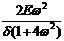 sin w t.
sin w t.
Таким образом, общее решение данного линейного неоднородного уравнения спостоянными коэффициентами имеет вид
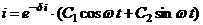 +
+  cos w t +
cos w t +  sin w t,
sin w t,
где 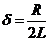 ,
, 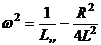 . Подставив начальные условия, получим частное решение этого уравнения.
. Подставив начальные условия, получим частное решение этого уравнения.
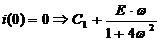 ;
; 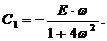
Для использования второго начального условия продифференцируем по переменной t:
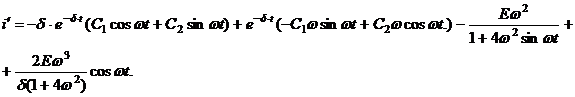
По условию задачи 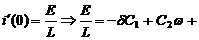
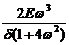 .
. 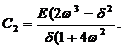 Частное решение уравнения имеет вид
Частное решение уравнения имеет вид
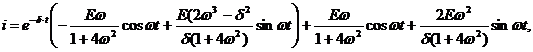
где