Пусть G – конечный н-граф.
Маршрутом в G называется последовательность ребер, в которой каждые два соседних ребра имеют общую вершину:
.
Число ребер в маршруте называется его длиной.
Маршрут М называется маршрутом общего вида, если вершины и ребра повторяются, цепью – если его ребра не повторяются, простой цепью – если его вершины не повторяются,
Маршрут, в котором совпадают начальная и конечная вершины, то есть 
, называется циклическим (замкнутым).
Циклический маршрут М называется маршрутом общего вида, если вершины и ребра повторяются, циклом – если его ребра не повторяются, простым циклом – если его вершины не повторяются (кроме начала и конца).
Граф, не содержащий циклов, называется ациклическим.
Вершины 
и 
называются связными, если существует маршрут с началом в и концом в .
Утверждение: Отношение связности вершин графа является отношением эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества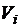 
.
Если классов разбиения больше одного, то все подграфы G (Vi) этого графа не связаны маршрутами друг с другом и называются связными компонентами графа.
Граф называется связным, если для любых двух различных вершин существует маршрут, соединяющий их. У связного графа одна компонента связности.
Расстоянием между вершинами a и b называется длина минимальной простой цепи, связывающей их. Расстояние обозначается d (a, b). Расстояние удовлетворяет аксиомам метрики.
Аксиомы метрики:
1) d (a, b) = d (b, a);
2) d (a, b) ≥ 0, d (a, b) = 0 ↔ a = b;
3) d (a, b) ≤ d (a, c) + d (c, b)
Матрица расстояний, это симметричная квадратная матрица размерности 
, строки и столбцы которой соответствуют вершинам графа, а на пересечении строк и столбцов записано расстояние между вершинами 
.
| 
| … | 
| 
| |
|
| 
| 
| … | 
| 
|
|
| 
|
| … | 
| 
|
| … | … | … | … | … | … |
|
| 
| 
| … | 
| 
|
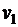
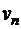
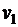
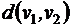
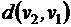
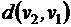
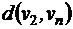
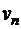
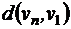
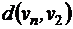
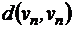
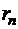
В последнем столбце матрицы указан эксцентриситет для каждой вершины – расстояние от данной вершины до наиболее удаленной вершины.
. (7.1)
Диаметр графа G – максимальное расстояние между вершинами графа. Диаметр находится по формуле:
.
Используя найденные эксцентриситеты вершин, диаметр можно найти по формуле:
. (7.2)
Радиус графа G – минимальное значение эксцентриситета. Радиус находится по формуле:
. (7.3)
Центр графа G – такая вершина, для которой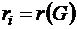 
.
Замечание: Центр в графе может быть не единственный.
Диаметральная цепь графа G – простая цепь, длина которой равна диаметру, соединяющая наиболее удаленные вершины графа.
Радиальная цепь графа G – простая цепь, длина которой равна радиусу, соединяющая центр и наиболее удаленную от него вершину графа.
Пример 7.1.
Для н-графа, приведенного на рисунке 7.1, записать 1) маршрут общего вида, 2) не простую цепь, 3) простую цепь, 4) циклический маршрут общего вида,5) не простой цикл, 6) простой цикл.
Решение.
1) Маршрут общего вида – это маршрут, в котором начальная и конечная вершина различны, и некоторые ребра повторяются. М 1 = (1, 4, 5, 1, 4, 7, 3). Здесь повторяется ребро (1, 4).
2) Не простая цепь – это маршрут, в котором не повторяются ребра, но повторяются вершины. М 2 = (4, 3, 1, 5, 6, 7, 4, 1). Здесь повторяется вершина 1.
3) Простая цепь – это маршрут, в котором не повторяются вершины. М 3 = (4, 3, 7, 5, 6).
4) Циклический маршрут общего вида – это маршрут, в котором начальная и конечная вершины совпадают, и некоторые ребра повторяются. М 4 = (1, 5, 4, 3, 1, 5, 7, 4, 1). Здесь повторяется ребро (1, 5).
Рисунок 7.1. Построение маршрутов
в неориентированном графе
5) Непростой цикл – это циклический маршрут, в котором не повторяются ребра, но повторяются вершины. М 5 = (3, 4, 5, 7, 4, 1, 3). Здесь повторяется вершина 4.
Заметим, что непростой цикл бывает только в графах, в которых существует конфигурация типа «песочные часы».
6) Простой цикл – это циклический маршрут, в котором не повторяются вершины. М 6 = (5, 4, 3, 2, 1, 5).
Пример 7.2.
Для н-графа, приведенного на рисунке 7.1, построить матрицу расстояний. Определить диаметр и радиус графа. Указать центры графа. Записать диаметральные и радиальные цепи
Решение:
Для построения матрицы расстояний, сопоставим строки и столбцы вершинам. На пересечении строк и столбцов укажем расстояние между соответствующими вершинами.
| d (a, b) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |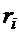 
|
| 1 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | 2 |
| 2 | 1 | 0 | 1 | 2 | 2 | 3 | 2 | 3 |
| 3 | 1 | 1 | 0 | 1 | 2 | 2 | 1 | 2 |
| 4 | 1 | 2 | 1 | 0 | 1 | 2 | 1 | 2 |
| 5 | 1 | 2 | 2 | 1 | 0 | 1 | 1 | 2 |
| 6 | 2 | 3 | 2 | 2 | 1 | 0 | 1 | 3 |
| 7 | 2 | 2 | 1 | 1 | 1 | 1 | 0 | 2 |
На месте (1, 1) стоит 0, так как кратчайший маршрут между вершиной 1 и вершиной 1 – это вырожденный маршрут (без ребер) длины 0.
На месте (1, 2) стоит 1, так как кратчайший маршрут между вершиной 1 и вершиной 2 – это единственное ребро, связывающее эти вершины.
На месте (1, 6) стоит 2, так как кратчайшая простая цепь, между вершиной 1 и вершиной 6 – это цепь из двух ребер (1, 5, 6). Значит, расстояние между этими вершинами равно 2.
И так далее.
В последнем столбце таблицы указано расстояние от данной вершины до наиболее удаленной от нее вершины – эксцентриситет. Это максимальное значение в строке.
Максимум значений последнего столбца – диаметр графа. Откуда d (G) = 3.
Минимум значений последнего столбца – радиус графа. Откуда r (G) = 2.
Центрами являются вершины: 1, 3, 4, 5, 7 (выделено красным). Их эксцентриситеты минимальны и равны радиусу графа.
Для построения диаметральных цепей выясним с помощью матрицы расстояний, какие вершины наиболее удалены друг от друга. Так как максимальное расстояние между вершинами – это диаметр графа, значит, найдем вершины, находящиеся на расстоянии, равном диаметру, то есть 3 (выделено синим). Это вершины 2 и 6. Следовательно, все диаметральные цепи в графе связывают эти вершины. Таких цепей две:
D 1 = (2, 1, 5, 6) и D 2 = (2, 3, 7, 6).
Для построения радиальных цепей выясним с помощью матрицы расстояний, какие вершины наиболее удалены от центров.
От центра 1 на расстоянии радиуса, равного 2, находятся вершины 6 и 7 (выделено зеленым). Значит можно провести радиальные цепи:
R 1 = (1, 5, 6) и R 2 = (1, 4, 7).
От центра 3 на расстоянии радиуса находятся вершины 5 и 6 (выделено зеленым). Значит можно провести радиальные цепи:
R 3 = (3, 4, 5) и R 4 = (3, 7, 6).
Далее аналогично.
