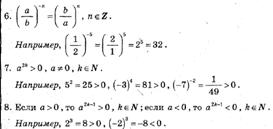Теория 5 класс
1) Натуральные числа - это числа, которые используют при счете. Множество натуральных чисел обозначают N. Все числа состоят из цифр, всего цифр 10: 0 1 2 3 4 5 6 7 8 9. 
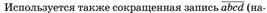
2)
3) 
1) 
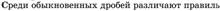
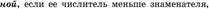
2)
3) Приведение дроби к общему знаменателю, алгоритм: 1)делим больший знаменатель на меньший, если делиться, то дополнительный множитель найден!2) если не делится, то больший знаменатель умножаем на 2, 3, 4 и т.д. до тех пор, пока больший знаменатель не разделится на меньший. Пример:30 не: на 24, поэтому 30∙2=60 не: на 24, 30∙3=90 не: на 24, 30∙4=120: 24=5- это дополнительный множитель к дроби с меньшим знаменателем, а 4- это дополнительный множитель к дроби с большим знаменателем.
4) 
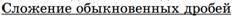
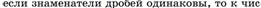
5) 
6) 
знаменатели 
и 
и 
7) 
первую дробь переписываем, вторую переворачиваем, а затем перемножаем дроби.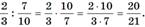 
8) 
2●5=10, 2●2●5●5=4●25=100
2●2●2●5●5●5=8●125=1000 и т. д.
9) 
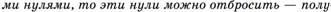
10) 
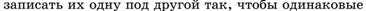
11) 
12) 
13) Чтобы разделить одну десятичную дробь на другую, переносим запятую вправо и в делимом, и в делителе на столько знаков, сколько их в делителе после запятой 0,1218: 0,058
14) 
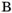
15) 
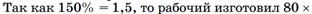
Пример 2: 
Так как 138 стр. – это 23%, то 138:23=6(стр)-в 1 %, значит 6·100=600(стр)-всего в книге. Можно решить эту задачу при помощи пропорции: 138стр – 23%
Х стр – 100%, х= 
=600(стр).
16) Средним арифметическим чисел называют сумму этих чисел, делённую на число слагаемых. Пример: найти ср.арифм. чисел 4;3;2;2;3, 
=2,8.
Теория 6 класс
1) Координатная прямая. Возьмем обычную прямую. Назовем ее прямая x. Выберем на этой прямой точку отсчета O, а также стрелкой укажем положительное направление этой прямой. Таким образом, справа от точки O у нас будут положительные числа, а слева – отрицательные. Выберем масштаб, то есть размер отрезка прямой, равный единице. У нас получилась координатная прямая. Каждому числу соответствует определенная единственная точка на этой прямой. Причем это число называют координатой этой точки. Поэтому прямая и называется координатной. А точка отсчета O называется началом координат.
К примеру, точка B находится на расстоянии 2 правее начала координат. Точка D находится на расстоянии 4 левее начала координат. Соответственно точка B имеет координату 2, а точка D координату -4. Сама точка O, будучи точкой отсчета, имеет координату 0 (нуль). Записывается это обычно так: O(0), B(2), D(-4). А чтобы постоянно не говорить «точка D с координатой такой-то», говорят проще: «точка 0, точка 2, точка -4». А саму точку при этом достаточно обозначить ее координатой. 
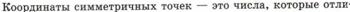
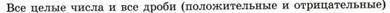
Зная координаты двух точек координатной прямой, мы всегда можем вычислить расстояние между ними. Допустим, у нас две точки A и B с координатами a и b соответственно. Тогда расстояние между ними будет |a - b|. Запись |a - b| читается как «a минус b по модулю» или «модуль разности чисел a и b».
2) Модуль. Алгебраически модуль числа x – это неотрицательное число. Обозначается как |x|. Причем если x > 0, то |x| = x. Если x < 0, то |x| = -x. Если x = 0, то |x| = 0. Геометрически модуль числа x – это расстояние между точкой и началом координат.
3) Сложение и вычитание чисел. 
..
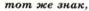
Примеры:2+3=5, -2-3= -5,-2+3=1, 2-3= - 1.
4) Числовые промежутки. 
5) Умножение и деление. 
. 
При делении все аналогично.
6) 
. 
7) Раскрытие скобок. 
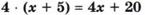
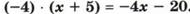
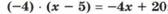
8) Упрощение выражений.
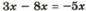
9) Решение уравнений. Алгоритм решения уравнения:
Уравнение решай в столбик! Все промежуточные вычисления в столбик выполняй справа от уравнения!
10) Задачи на дроби. 
Примеры:1) 
2) 
11) 
| Признак делимости на 2 Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной. Признак делимости на 3 Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Признак делимости на 4 Число делится на 4 тогда и только тогда, когда число из двух последних его цифр нули или делится на 4. Признак делимости на 5 Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5). Признак делимости на 6 Число делится на 6 тогда и только тогда, когда оно делится на 2 и на 3. Признак делимости на 7 Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7). Признак делимости на 8 Число делится на 8 тогда и только тогда, когда три его последние цифры - нули или образуют число, которое делится на 8. | Признак делимости на 9 Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9. Признак делимости на 10 Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль. Признак делимости на 11 Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками делится на 11 (то есть 182919 делится на 11, так как 1 - 8 + 2 - 9 + 1 - 9 = -22 делится на 11) Признак делимости на 12 Число делится на 12 тогда и только тогда, когда оно делится на 3 и на Признак делимости на 14 Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7. Признак делимости на 15 Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5. Признак делимости на 25 Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75)или число кратно 5. |
12)Пропорция. 
Теория по геометрии
Основные фигуры:точка, прямая, плоскость. Точки обозначают прописными, а прямые строчными буквами латинского алфавита.
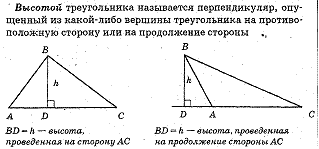
Площадь треугольника
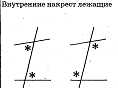
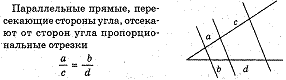
Теория 7 класс и функции
