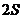Произвольный треугольник
1. Теорема косинусов:  2. Теорема синусов:
2. Теорема синусов: 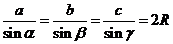 3. Площадь определяется по формуле:
3. Площадь определяется по формуле: 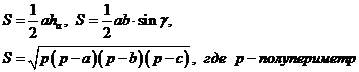
|
 


|
Три медианы пересекаются в одной точке (её называют центром тяжести или центроидом треугольника) и делятся этой точкой в отношении 2: 1, считая от вершины. Длину медианы можно определить по формуле: 
|   
 
|
Три высоты треугольника пересекаются в одной точке (её называют ортоцентром треугольника)
Для любого треугольника справедливо соотношение:

|

|
Три биссектрисы треугольника пересекаются в одной точке (центр вписанной в треугольник окружности)
Длину биссектрисы можно определить по формуле:

|
Свойство биссектрисы:
  

|
Около всякого треугольника можно описать окружность. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника, а её радиус определяется по формулам: 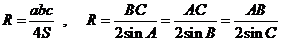
|   
 
  
|
Во всякий треугольник можно вписать окружность. Центр вписанной окружности лежит на пересечении биссектрис, а её радиус вычисляется по формуле:
 , , 
|
     
|
Для правильного треугольника со стороной  Площадь:
Площадь: 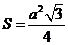 , высота: , высота:  Радиус вписанной окружности:
Радиус вписанной окружности:  ,
Радиус описанной окружности: ,
Радиус описанной окружности: 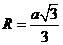 , ,
|
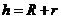
     
|
| Для прямоугольного треугольника с катетами  и гипотенузой и гипотенузой  справедливы соотношения: справедливы соотношения:
  (теорема Пифагора), (теорема Пифагора), 
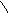 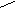

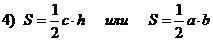
 
  
|
 5) Центр описанной окружности лежит на середине гипотенузы, а её радиус вычисляется по формуле: 5) Центр описанной окружности лежит на середине гипотенузы, а её радиус вычисляется по формуле: 
 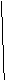
 
| 6) радиус вписанной окружности вычисляется по формуле: 
 
    
|
Для равнобедренного прямоугольного треугольника:

|    
|
Произвольный четырёхугольник
1) Если окружность вписана в четырёхугольник со сторонами 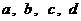 , то суммы длин противоположных сторон равны: , то суммы длин противоположных сторон равны: 
|  
  
|
2) Если окружность описана около четырёхугольника, то суммы его противоположных углов равны  : :
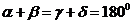
   3) Площадь любого четырёхугольника вычисляется по формулам: 3) Площадь любого четырёхугольника вычисляется по формулам:
   , где , где  - -
длины диагоналей,  - угол между диагоналями. - угол между диагоналями.
  , где , где  - полупериметр, - полупериметр,  - радиус - радиус
вписанной окружности
|
    
|
Параллелограмм
1) Сумма квадратов диагоналей равна сумме квадратов его сторон: 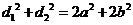 2) площадь вычисляется по формулам:
2) площадь вычисляется по формулам:

|        
|
Ромб
1) Диагонали ромба взаимно перпендикулярны и являются биссектрисами его
углов.
2) Площадь вычисляется по формулам:

|           
|
| 
Квадрат
       1) 1) 
2) 

|
 Прямоугольник Прямоугольник
      1) 1)  2) Около любого прямоугольника
2) Около любого прямоугольника
можно описать окружность, 
|
|
Трапеция
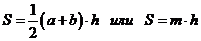 , где
, где  - средняя линия. В равнобедренной трапеции
- средняя линия. В равнобедренной трапеции
Средняя линия  проекция диагонали на нижнее
проекция диагонали на нижнее
основание, равна средней линии,
MN = AH








Правильный шестиугольник
   
  
1) 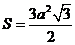 , ,  2)
2) 
|
Окружность
-
    Свойства касательных к окружности. Свойства касательных к окружности.   а) Радиус, проведённый в точку касания, а) Радиус, проведённый в точку касания,
      перпендикулярен касательной; перпендикулярен касательной;
б) Две касательные к окружности,
проведённые из одной точки, равны,
   а центр окружности лежит на биссектрисе а центр окружности лежит на биссектрисе
угла между ними.
  2. Измерение углов, связанных с окружностью. 2. Измерение углов, связанных с окружностью.
а) Центральный угол измеряется дугой,
на которую он опирается;
б) Вписанный угол измеряется половиной дуги,
  на которую он опирается; на которую он опирается;
  
в) Угол между касательной и хордой равен половине
дуги, заключённой между касательной и хордой.
  3. Метрические соотношения в окружности. 3. Метрические соотношения в окружности.
а) Если две хорды пересекаются, то произведение
 отрезков одной хорды равно произведению отрезков отрезков одной хорды равно произведению отрезков
другой хорды: АМ  ВМ = СМ ВМ = СМ  DМ DМ
|

 б) Если из точки М к окружности проведены б) Если из точки М к окружности проведены
две секущие, то АМ  ВМ = СМ ВМ = СМ  DМ DМ
 в) Если из точки М к окружности проведены в) Если из точки М к окружности проведены
секущая и касательная, то АМ  ВМ = СМ 2 ВМ = СМ 2
|
   4. Площадь круга: 4. Площадь круга: 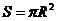 , ,
  Длина окружности: Длина окружности: 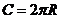
 Площадь сектора: а) Площадь сектора: а) 
б) 
Длина дуги сектора: а) 
б) 
|
|
Некоторые свойства площадей:
а) Отношение площадей подобных фигур равно квадрату
   коэффициента подобия: коэффициента подобия: 
б) Отношение площадей двух треугольников с одинаковыми
высотами равно отношению их оснований.
 
 в) Биссектриса треугольника делит его площадь на в) Биссектриса треугольника делит его площадь на
части, пропорциональные сторонам, между которыми
она проведена. 
|
 2. Теорема синусов:
2. Теорема синусов: 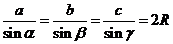
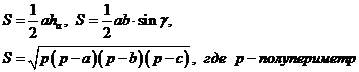

















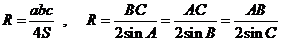








 ,
, 






 Площадь:
Площадь: 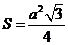 , высота:
, высота:  Радиус вписанной окружности:
Радиус вписанной окружности:  ,
Радиус описанной окружности:
,
Радиус описанной окружности: 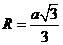 ,
,
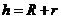







 (теорема Пифагора),
(теорема Пифагора), 



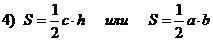



 5) Центр описанной окружности лежит на середине гипотенузы, а её радиус вычисляется по формуле:
5) Центр описанной окружности лежит на середине гипотенузы, а её радиус вычисляется по формуле: 












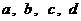 , то суммы длин противоположных сторон равны:
, то суммы длин противоположных сторон равны: 





 :
:
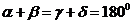


 3) Площадь любого четырёхугольника вычисляется по формулам:
3) Площадь любого четырёхугольника вычисляется по формулам:

 , где
, где  -
- - угол между диагоналями.
- угол между диагоналями.





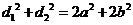 2) площадь вычисляется по формулам:
2) площадь вычисляется по формулам:



























 1)
1) 






 1)
1) 


















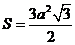 ,
, 






 Свойства касательных к окружности.
Свойства касательных к окружности. 
 а) Радиус, проведённый в точку касания,
а) Радиус, проведённый в точку касания,



 перпендикулярен касательной;
перпендикулярен касательной;

 а центр окружности лежит на биссектрисе
а центр окружности лежит на биссектрисе
 2. Измерение углов, связанных с окружностью.
2. Измерение углов, связанных с окружностью.
 на которую он опирается;
на которую он опирается;




 3. Метрические соотношения в окружности.
3. Метрические соотношения в окружности. отрезков одной хорды равно произведению отрезков
отрезков одной хорды равно произведению отрезков ВМ = СМ
ВМ = СМ  DМ
DМ

 б) Если из точки М к окружности проведены
б) Если из точки М к окружности проведены ВМ = СМ
ВМ = СМ  DМ
DМ


 в) Если из точки М к окружности проведены
в) Если из точки М к окружности проведены
 ВМ = СМ 2
ВМ = СМ 2

 4. Площадь круга:
4. Площадь круга: 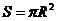 ,
,
 Длина окружности:
Длина окружности: 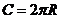
 Площадь сектора: а)
Площадь сектора: а) 





 коэффициента подобия:
коэффициента подобия: 



 в) Биссектриса треугольника делит его площадь на
в) Биссектриса треугольника делит его площадь на 


 - периметр перпендикулярного сечения,
- периметр перпендикулярного сечения,  - длина бокового ребра
- длина бокового ребра

 - периметр основания,
- периметр основания,
 - длина бокового ребра
- длина бокового ребра

 - измерения параллелепипеда (длина, ширина, высота)
- измерения параллелепипеда (длина, ширина, высота)






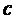

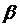
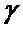



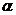





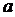
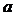
 и гипотенузой
и гипотенузой  справедливы соотношения:
справедливы соотношения: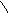
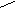
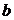





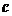










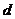




 , где
, где  - полупериметр,
- полупериметр, 
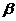




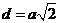



 Прямоугольник
Прямоугольник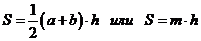 , где
, где  - средняя линия. В равнобедренной трапеции
- средняя линия. В равнобедренной трапеции проекция диагонали на нижнее
проекция диагонали на нижнее