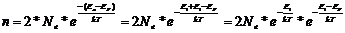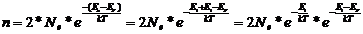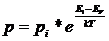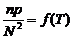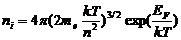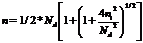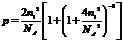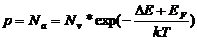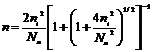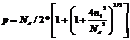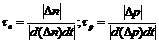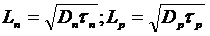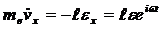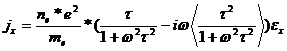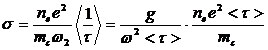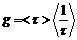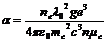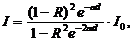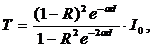Основные параметры полупроводниковых материалов

К важнейшим параметрам, которые характеризуют основные электрофизические свойства полупроводниковых веществ, относятся:

—удельное электрическое сопротивление (проводимость) материала;

— температурный коэффициент удельного сопротивления (проводимости) вещества;

— ширина запрещенной зоны и энергии активации примесей;

— концентрация, время жизни носителей заряда;

— коэффициенты диффузии электронов и дырок, диффузионная длина;

— подвижность основных носителей заряда в полупроводнике.

В ряде случаев специального применения к этим параметрам добавляются и другие, например, коэффициент термо-электродвижущей силы (при использовании термоэлектрических эффектов в полупроводниках), коэффициент Холла и т. д.

а) Концентрация и время жизни, носителей заряда в полупроводниках

Как уже отмечалась, между процессами генерации и рекомбинации носителей заряда при любой температуре устанавливается динамическое равновесие, которому соответствуют равновесные концентрации носителей заряда, обозначаемые обычно через n₀, p₀. В случае собственного полупроводника концентрация электронов в зоне проводимости равна концентрации дырок в валентной зоне: n₀,=p₀=n_i В состоянии термодинамического равновесия в невырожденном полупроводнике произведение равновесных концентраций основных и неосновных носителей заряда при заданной температуре является величиной постоянной, равной квадрату концентрации электронов (или дырок) в собственном полупроводнике при этой же температуре:

n_n,*n_p=n_i² = const                                                              (4.6)

Это соотношение легко получить следующим образом, учитывая соотношения (4.2) — (4.5):

 

(4.7)

 

 

Аналогично

 

Перемножив эти два выражения и учтя, что n_i= p_i, получим выражение (4.6).

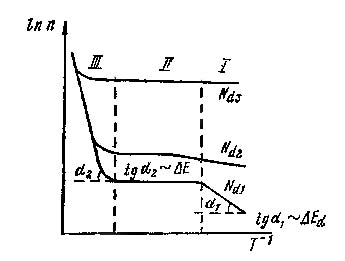
Концентрация носителей в полупроводнике, например n-типа, зависит от температуры и концентрации примесей (рис. 4.6). В области низких температур (область I) рост концентрации носителей заряда связан с интенсификацией процессов ионизации примеси. Наклон прямой в этой области определяется энергией активации примесей. С увеличением температуры число носителей, поставляемых примесями, возрастает до тех пор, пока не истощатся электронные ресурсы примесных атомов и не наступит область II область истощения примесей.

Рис. 4.6

В этой области примеси полностью ионизированы, а электроны еще не переходят через запрещенную зону и концентрация электронов в зоне проводимости остается практически постоянной величиной. Дальнейший рост температуры приводит к быстрому росту концентрации носителей вследствие перехода электронов через запрещенную зону — область III. Наклон этого участка кривой характеризует ширину запрещенной зоны полупроводника, а полупроводник можно считать собственным, так как концентрация носителей заряда определяется ионизацией собственных атомов полупроводника. Температура, при которой это происходит, т. е. начинается область III, будет тем меньше, чем меньше ширина запрещенной зоны полупроводника, и эта температура является максимальной рабочей температурой полупроводникового прибора, изготовленного из полупроводника с концентрацией примеси N_g. Угол наклона участка кривой в области I с увеличением концентрации примесей уменьшается, так как с увеличением концентрации примесей из-за взаимодействия примесных атомов происходит расщепление примесных энергетических уровней и уменьшение энергии ионизации примесей (∆E_g>∆E_g'>∆E_g''). При достаточно большой концентрации примесей N_g энергия ионизации примесей стремится к нулю, так как образовавшаяся примесная зона перекрывается зоной проводимости и полупроводник становится вырожденным.

Температура, соответствующая переходу от примесной электропроводности к собственной, увеличивается с увеличением концентрации примесей (например, T₃'>T₃). Это значит, что максимальная рабочая температура полупроводникового прибора, созданного на основе полупроводника с большей концентрацией примесей, будет также немного выше максимальной рабочей температуры такого же прибора из того же материала, но с меньшей концентрацией примесей.

Во многих случаях оказалось, что энергия, необходимая для перевода электрона с донорного уровня в зону проводимости, настолько мала, что при комнатных температурах все электроны с примесных уровней находятся уже в зоне проводимости. Если к тому же концентрация доноров намного превышает концентрацию собственных электронов, то количество носителей почти перестает зависеть от температуры и изменение электропроводности с температурой в этих условиях определяется, в основном, лишь температурной зависимостью подвижности.

Однако концентрацию носителей заряда в данном материале можно по желанию варьировать и при фиксированном содержании примесей. Одним из замечательных свойств полупроводников является наличие эффекта фотопроводимости. Это явление легко понять с помощью зонной модели. При поглощении кванта света, энергия которого достаточна для перевода электрона из состояния у потолка валентной зоны в зону проводимости, в обеих зонах появляются добавочные носители заряда и проводимость кристалла растет. Может иметь место также фотопроводимость, связанная с фотоионизацией примесных атомов, однако этот эффект менее значителен сравнительно с упомянутым выше в связи с тем, что концентрация примесей обычно во много раз меньше концентрации валентных электронов и, кроме того, примесные уровни заполнены лишь при низких температурах. Вместе с тем оказалось, что концентрация электронов и дырок в полупроводниках можно изменять и иными способами. Во-первых, путем инжекции носителей заряда в кристалл, например с помощью металлических электродов, и, во-вторых, при определенных условиях путем экстракции (удаления) носителей из кристалла электрическим полем.

В заключение приведем численный пример для иллюстрации относительного вклада различных механизмов электропроводности. В чистом германии собственная концентрация n_i, электронов и дырок при комнатной температуре представляет собой величину 2,5x10¹³ см^-3. Число атомов германия в единице объема равно 4,5x10²² см^-3. Следовательно, если в германии присутствует донорная примесь, которая при комнатных температурах полностью «ионизирована», то при наличии одного атома примеси на 10⁶ атомов германия мы получили бы n=4,5x10¹⁶ см^-3 электронов. Отсюда p=n_i²/n=1,4x10¹⁰ см^-3, так что, действительно, n>>p. Если температуру поднять до 300°С, то n_i = 1,5x10¹⁷см^-3 и преобладающей становится уже собственная концентрация носителей заряда.

Из этой оценки видно, что для того, чтобы германий сохранял свойства собственного полупроводника при комнатной температуре, примеси, образующие уровни вблизи зоны проводимости, могут присутствовать в кристалле в количестве не более одного атома примеси на 10⁹ атомов германия.

Рассмотрим распределение электронов по примесным уровням, лежащим между валентной зоной и зоной проводимости в примесном полупроводнике. Для проведения рассуждений поместим начало отсчета энергий на дно зоны проводимости. Если рассматривать генерацию и рекомбинацию электронов и дырок как химическую реакцию, приводящую к образованию нормального атома пли иона в кристалле N, то такую реакцию можно описывать уравнением

е+h = N+∆Е.                                                                (4.8)
Из закона действующих масс следует

(4.9)

где f(Т) имеет вид [F(Т)² ехр(—∆Е/kТ)], причем F(Т) — функция, медленно меняющаяся с температурой. Равенство (4.9) эквивалентно равенству np=N_c*N_v*ехр(-∆E/kТ)=n_i² в котором приводится вид функции F(Т). Если нам известна концентрация электронов в зоне проводимости, то очень легко проверить степень вырождения в полупроводнике. Пусть для примера Е=300 К., тогда при m_e≈m_n≈m₀ величина N_c 2,5x10¹⁹ см^-3. Поэтому в области концентраций n<10^{19 см-3} для Е_F получаем Е_F < 2kТ, т.е. электронный газ невырожден. С другой стороны, если n≈2x10¹⁹см^-3, то Е_F> 2kT и исходное предположение перестает быть справедливым, т.е. наступает вырождение электронов в зоне проводимости. Если m_e<<m₀ как это имеет место в InSb, то вырождение в зоне проводимости наступает при значительно меньших концентрациях электронов.

Прежде чем приступить к исследованию более сложных случаев, рассмотрим полупроводник, содержащий N_d донорных уровней в единице объема. Предположим, что донорные уровни расположены в непосредственной близости от дна зоны проводимости, так что энергия ионизации примесей ε_d очень мала по сравнению с шириной запрещенной зоны; мы уже видели, что такие уровни довольно типичны, например в Ge, где ε_d ≈0,01 эВ при ∆Е = 0,7эВ. Предположим также, что уровень Ферми расположен существенно ниже дна зоны проводимости, т. е. Е_F <<-kТ. Вследствие малости ε_d практически все атомы примеси будут ионизированными и их электроны окажутся в зоне проводимости. Выясним сперва, какова предельная концентрация примесей, при которой эти условия перестают быть справедливыми. Для начала допустим, что N_d>>n_i, так что можно пренебречь «собственными электронами», т. е. теми, которые перебрасываются в зону проводимости из валентной зоны. В этом случае мы имеем простое соотношение n=N_d. В этих условиях число электронов в зоне проводимости будет слабо зависеть от температуры.

Положение уровня Ферми в этих условиях определяется уравнением

n=N_d=N_c*exp(Е_F/kt)

или

Е_F=kT*ln(N_d/N_c)                                               (4.10)

Формула (4.10) справедлива лишь при условии Е_F <-kТ, т.е. при N_d<N_c/2. Для Ge при Т=300 К это означает, что для применимости равенства (4.10) требуется, чтобы N_d < <10¹⁹ см^-3; с другой стороны, однако, должно выполняться условие N_d >10¹⁴ см^-3, чтобы можно было пренебречь концентрацией собственных носителей заряда. Итак, в Ge при комнатных температурах существует довольно широкая область значений N_d, для которых выполняются условия примесного истощения.

Из формулы (4.10) следует, что с ростом N_d уровень Ферми перемещается вверх примерно с середины запрещенной зоны до значения энергии примерно на kT ниже дна зоны проводимости, когда N_d→N_c. Если N_d≥N_c, то система электронов в зоне проводимости становится вырожденной и для определения положения уровня Ферми необходимо воспользоваться уже равенством типа

 

В этом случае полупроводник будет вести себя скорее как металл.

Интересно выяснить, что происходит в более общем случае, когда N_d того же порядка величины, что и n_i,, но при этом N_d << N_c. Ясно, что, если ∆Е>>kТ, уровень Ферми будет находиться достаточно далеко от дна зоны проводимости, на основании чего по-прежнему можно предполагать, что все атомы примеси ионизированы. Тогда между n и р имеет место простое соотношение

n-р= N_d                                                                                 (4.11)

выражающее условие электрической нейтральности полупроводника. На основании равенства (4.11) можно выразить n и р через n_i, и N_d и получить

(4.12)

 

Если N_d>>n_i, (а также N_d<N_c), то приближенно имеем

 

N= N_d + n_i²/N_d                                                              (4.13)

P= n_i/N_d

Заметим, что концентрация дырок в этом случае намного меньше концентрации дырок в собственном веществе (в отношении n_i/N_d). Например, при n_i=2,37x10¹³ см^-3 (как для Gе) и N_d=10¹⁶ см^-3 мы получаем n≈10¹⁶ см^-3 и р≈ 5,6x10¹⁰ см^-3. В этом случае электроны являются основными носителями заряда, а дырки — не основными. Несмотря на малость концентрации не основных носителей по сравнению с концентрацией основных, первые могут играть в известных условиях очень важную роль. Предположив, что имеет место обратное неравенство N_d<<n_i/, мы приближенно получаем

n=n_i+1/2 N_d                                                                                 (4.14)

p=n_i-1/2 N_d

Предположим теперь, что вместо донорной примеси имеется N_a акцепторных атомов в единице объема, уровни энергии которых расположены непосредственно над потолком валентной зоны. Аналогично предыдущему будем считать, что уровень Ферми расположен выше потолка валентной зоны по крайней мере на несколько kТ. Тогда почти все акцепторные уровни будут заняты электронами из валентной зоны, т. е. примесные атомы будут «ионизированными», причем в валентной зоне останется около N_а свободных дырок, и мы получим

                                                                                                                   (4.15)

Эта формула справедлива лишь при условии, что отношение N_a/N_v ≤1/2. Снова с ростом N_a от 0 до N_v„ уровень Ферми смещается примерно с середины запрещенной зоны до потолка валентной зоны.

Ясно, что вместо равенства (4.11) теперь имеем

p-n= N_a                                                         

которое даст             

                                                                                                                              (4.16)

 

 

                                                                                                           (4.17)

При N_a>>n_i, приближенно имеем

n=n_i²/N_a                                                                                    (4.18)

p=N_a+ n_i²/N_a

Если же n_i >>N_a, то приближенно

n=n_i²-1/2*/N_a                                                                              (4.19)

p= n_i + 1/2*N_a

Допустим теперь, что в кристалле одновременно присутствуют как донорные, так и акцепторные примеси. Предположим вначале, что (N_d-N_a>>n_i. При N_а=0 уровень Ферми окажется существенно выше середины запрещенной зоны. При добавлении в кристалл акцепторов вероятность заполнения соответствующих им уровней, т.е. вероятность «ионизации» акцепторных атомов, очень велика, поскольку эти акцепторные уровни лежат значительно ниже уровня Ферми. Электроны, заполняя акцепторные уровни (по одному электрону на уровень), переходят с донорных уровней или из зоны проводимости. Число свободных дырок чрезвычайно мало, так как уровень Ферми располагается достаточно высоко над краем валентной зоны. Поэтому эффективное число доноров равно N_d-N_a и положение уровня Ферми определяется из соотношения

N_d-N_a= N_с*exp(Е_F/kТ).                                                              (4.20)

При N_a → N_d акцепторы все в большей степени нейтрализуют действия доноров и уровень Ферми постепенно перемещается к середине запрещенной зоны. При N_a > N_d эффективное число акцепторов становится равным N_a-N_d, все электроны с донорных центров переходят на акцепторные уровни, уровень Ферми опускается еще ниже и в пределе оказывается у самого.края валентной зоны. Зависимость Е_F от концентрации

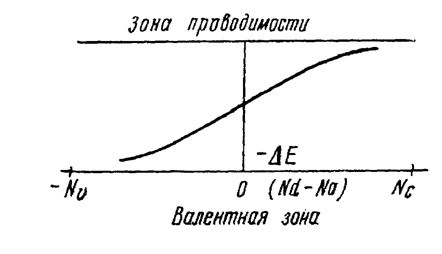
Рис. 4.7

примесных атомов показана на рис. 4.7 (фактический ход кривой зависит от температуры). Серия кривых, изображающих температурную зависимость n и р при различных значениях Nd-Na  для Gе, представлена на рис. 4.8.

В переходных процессах до установления термодинамического равновесия концентрация носителей может превысить равновесную на величину, равную ∆n(∆p), которую называют избыточной концентрацией. После прекращения энергетического воздействия на полупроводник избыточная концентрация носителей заряда в нем из-за процесса рекомбинации через некоторое время уменьшится до нуля. Количество носителей заряда, рекомбинирующих в единицу времени в единице объема (быстрота изменения концентрации), пропорционально избыточной концентрации и обратно пропорционально некоторому параметру τ, который называют временем жизни неравновесных носителей:

 

-dn/dt=-d(∆n)/dt=∆n/τ_n; -dp/dt=-d(∆p)/dt=∆p/τ_p                                                         (4.21)

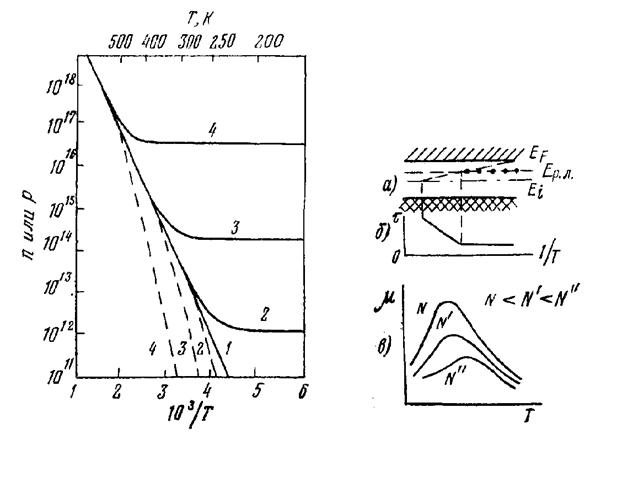
Рис.4.8                                                              Рис.4.9

Таким образом, временем жизни неравновесных носителей заряда является отношение избыточной концентрации (∆n или ∆р) неравновесных носителей заряда к скорости изменения этой концентрации вследствие рекомбинации:

(4.22)

Это время, в течение которого перавновесная концентрация носителей уменьшается в е раз.

Время жизни неравновесных носителей заряда зависит от температуры полупроводника. Рассмотрим температурную зависимость времени жизни на примере полупроводника с электропроводностью n-типа с рекомбинационными ловушками в верхней половине запрещенной зоны (рис. 4.9, а и 4.9,6). При очень низкой температуре рекомбинационные ловушки заполнены электронами, так как вероятность их заполнения, судя по положению уровня Ферми, намного больше 50%. При этом первый этап рекомбинации (захват дырки рекомбинационной ловушкой) происходит быстро и время жизни оказывается небольшим. С повышением температуры уровень Ферми смещается вниз и находится вблизи энергетических уровней рекомбинационных ловушек. Это означает, что теперь не все ловушки заполнены электронами, т.е. не все ловушки могут захватить блуждающие по полупроводнику дырки. Поэтому с повышением температуры время жизни растет.

б) Подвижность носителей заряда в полупроводниках

На величину подвижности носителей заряда в основном влияют следующие факторы:

1) тепловые колебания атомов или ионов кристаллической решетки;

2) примеси в полупроводниковом или нейтральном состояниях;

3) всевозможные дефекты решетки (пустые узлы, искажения, вызванные атомами внедрения, дислокации, трещины, границы кристаллов и т.д.).

Рис. 4.9, в иллюстрирует температурную зависимость подвижности носителей заряда. В диапазоне малых температур с уменьшением температуры уменьшаются тепловые скорости хаотического движения носителей заряда, что приводит к увеличению времени пребывания носителя вблизи иона примеси, т. е. увеличивается длительность воздействия электрического поля иона примеси на носитель заряда. Поэтому в диапазоне малых температур с уменьшением температуры подвижность носителей также уменьшается.

При увеличении концентрации примесей увеличивается рассеяние на полях примесей, т.е. уменьшается подвижность носителей заряда. Однако в диапазоне высоких температур преобладающим механизмом рассеяния носителей, даже при большой концентрации примесей, остается рассеяние на тепловых колебаниях атомов кристаллической решетки и соответственно кривые температурной зависимости подвижности носителей заряда практически не смещаются с увеличением концентрации примесей. В этом диапазоне температур преобладает рассеяние носителей заряда на тепловых колебаниях атомов кристаллической решетки и поэтому подвижность носителей уменьшается (рис. 4.9, в). Если в рассеянии носителей заряда участвуют оба механизма (колебательно-решеточный и ионный) с преобладанием того или другого в различных интервалах температуры, то результирующая температурная зависимость подвижности имеет максимум, который смещается в область высоких температур при увеличении концентрации примесей.

в) Электропроводность полупроводников

Электропроводность полупроводников обусловлена дрейфом носителей обоих знаков: электронов и дырок.

Удельная электрическая проводимость собственного полупроводника определяется по формуле

γ_собств=γ_n+γ_p=q n μ_n+q p μ_p=qn_i*(μ_n+μ_p)                                                    (4.23)

где γ_n— электропроводность, обусловленная передвижением электронов в зоне проводимости; γ_p — электропроводность, обусловленная передвижением дырок в валентной зоне; μ_n, μ_p — их подвижность.

Удельная проводимость примесного полупроводника n-типа равна сумме собственной и примесной электропроводности:

γ_n = γ_пр + γ_собств; γ_пр =n_Д q μ_n                                                                                 (4.24)

Через n_Д обозначена концентрация свободных электронов, образовавшихся за счет ионизации донорной примеси. В дырочном полупроводнике

γ_p = γ_пр + γ_собств; γ_пр =p_a q μ_p                                                                                  (4.25)

Через p_a обозначена концентрация дырок, образовавшихся за счет ионизации акцепторной примеси.

Анализируя результаты хода температурной зависимости концентрации и подвижности носителей заряда в полупроводниках, можно представить и общие закономерности в изменении удельной проводимости полупроводниковых материалов от температуры.

В предыдущих параграфах было отмечено, что концентрации носителей заряда в широком диапазоне температур изменяются по экспотенциальному закону, в то время как подвижность — лишь по степенному. Следовательно, температурная зависимость электропроводности как в собственных, так и примесных полупроводниках определяется, в основном, температурной зависимостью концентрации свободных носителей заряда и может быть представлена в виде

γ_i=γ₀e^-ΔE/2kT                                                                                 (4.26)

для собственных полупроводников,

γ_n=γ₀e^-ΔEa/2kT                                                                                    (4.27)

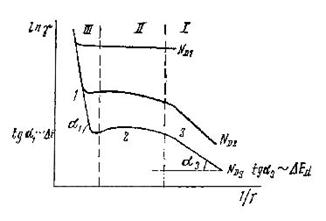
для примесных полупроводников (в данном случае для полупроводника n-типа). В выражениях (4.26), (4.27) - γ₀ — постоянная, определяемая природой материала.

Рис. 4.10

В интервале средних значений температур (участок 2, рис. 4.10), соответствующих полному истощению примеси, концентрация основных носителей практически не меняется при увеличении температуры. Поэтому температурная зависимость γ на этом участке определяется температурной зависимостью подвижности. Как видно из рисунка 4.10, температурный коэффициент удельного сопротивления полупроводниковых материалов в области I и II является отрицательной величиной, т.е. удельное электрическое сопротивление полупроводников уменьшается с ростом температуры в отличие от проводниковых материалов.

Зависимость удельной проводимости от напряженности электрического поля показана на рис. 4.11. В области I выполняется закон Ома, и электропроводность полупроводника не изменяется с ростом напряженности электрического поля. При превышении некоторого критического значения Е_кр (примерно 10⁴—10⁶ В/м) наблюдается отклонение от закона Ома на участке II вследствие термоэлектронной ионизации, в области III — вследствие ударной и электростатической ионизации, IV — вследствие пробоя.

Явление термоэлектронной ионизации заключается в том, то электрическое поле большой напряженности изменяет энергетическое состояние электронов так, что энергия, необходимая для перевода электронов в зону проводимости, уменьшается, а следовательно, возрастает вероятность тепловой генерации пар носителей заряда. В этом случае изменение концентрации носителей с ростом поля происходит по

экспоненциальному закону.

Рис. 4.11

Процесс ударной ионизации сводится к тому, что в сильных электрических полях носители заряда на длине свободного пробега могут приобрести энергию, достаточную для ионизации вещества. Это означает, что при столкновении носителей с атомами происходит генерация электронно-дырочных пар. В электрических полях большой напряженности (более 10⁸ В/м) может наблюдаться туннельный эффект, при котором благодаря волновым свойствам электронов возможен прямой переход их из валентной зоны в зону проводимости без увеличения энергии. Рассмотренные процессы термоэлектронной, ударной и электростатической ионизации, увеличивая концентрацию носителей заряда, не носят лавинообразного характера, так как уравновешиваются процессами рекомбинации. Однако в электрических полях напряженностью более 10⁸ В/м наблюдается лавинообразное нарастание числа носителей, приводящее к электрическому пробою.

Воздействие сильного электрического поля приводит не только к изменению концентрации свободных носителей заряда, но и к значительному изменению их подвижности. С изменением подвижности носителей заряда связаны явление разогрева электронно-дырочного газа и эффект Ганна.

Первое заключается в том, что свободные носители за счет увеличения скорости во внешнем электрическом поле обладают энергией, большей, чем равновесная тепловая энергия решетки. Такие носители называют «горячими». Под эффектом Ганна понимают явление, наблюдаемое в постоянном электрическом поле большой напряженности в некоторых полупроводниковых материалах и сводящееся к возникновению периодических колебаний тока, протекающего через образец.

Описанные выше явления лежат в основе работы многих полупроводниковых приборов: стабилитронах и лавинных диодах, нелинейных резисторах (варисторах), генераторах Ганна и др.

г) Диффузионная длина носителей заряда в полупроводниках

Если предположить, что в какой-либо точке или плоскости полупроводника создается избыточная по сравнению с равновесной концентрация электронов или дырок ∆n₀, то тогда избыточные (неравновесные) носители заряда будут диффундировать вглубь и по.мере удаления от этой точки их концентрация будет падать за счет рекомбинации по экспоненциальному закону

∆n(х) =∆n_0*e^-x/L                                                             (4.28)

где L — диффузионная длина, т.е. расстояние, на котором в однородном полупроводнике при одномерной диффузии в отсутствие электромагнитного поля избыточная концентрация носителей заряда уменьшается вследствие рекомбинации в e раз, т.е. это расстояние, на которое носитель диффундирует за время, равное времени жизни носителей заряда τ. Диффузионная длина связана со временем жизни неравновесных носителей следующими соотношениями:

                                                                                                           (4.29)

 

где D_n и D_p —.коэффициенты диффузии для электронов и дырок, определяемые как

D_n=Ф_n/grad n                                                                       (4.30)

В выражении (4.30) Ф_n — поток частиц при диффузии, т. е. число частиц, пересекающих в единицу времени единичную площадку, перпендикулярную направлению градиента их концентрации — grad n

Диффузионная длина является важным параметром полупроводниковых материалов, зависящим от наличия в них примесей, совершенства кристаллической решетки и т.д. Для германия и кремния эта величина указывается в паспорте данного материала.

Не следует путать диффузионную длину с длиной свободного пробега носителей заряда, которая определяется как среднее расстояние, проходимое носителем между двумя последовательными актами рассеяния.

д) Оптические свойства полупроводников

Для описания оптических параметров материалов обычно используют комплексны показатель преломления n*

n*=n (1—iκ)                                                          (4.31)

состоящий из действительной и мнимой частей. В таком слу­чае для плоской электромагнитной волны λ — длина волны, ν— частота), распространяющейся в направлении х:

Ψ=A*exp(2πiν*(t-n*x/c)                                                   (4.32)

можно записать

Ψ=A*exp(-2πνnκx/c)*exp(2πiν (t-nx/c))                           (4.33)

Фазовая скорость v = с/n, а длина волны λ, если поглощение не слишком велико, равна с/νn:

Ψ=A*exp(-αx/2)*exp(2πiν (t-x/v))                                    (4.34)

Α=4πκ/ λ= 4πnκ/λ₀                                                            (3 35)

где λ₀ — длина волны в вакууме при частоте ν; κ— показа­тель поглощения; α — коэффициент поглощения. Из классической электродинамики следует, что

ε*=ε – iσ/(2πνε₀)                                                                (4.36)

где  ε — обычная диэлектрическая проницаемость; σ — элект­ропроводность и (n*)² = ε*²:

ε=n2*(1-κ²)ε                                                                      (4.37)

σ=4πn² κνε₀)                                                                      (4.38)

при ε > 0

α= σ/(n² λ ν ε₀)= σ/(n c ε₀)                                                                         (4.39)

На частотах, недостаточно высоких, чтобы вызвать меж­зонные переходы или образование экситонов, поглощение обусловлено возбуждением колебаний решетки или переходами между состояниями в одной золе.

Уравнение движения электронов в переменном поле с час­тотой,ω/2 π в одномерном случае имеет вид

(4.40)

Вводя τ — время релаксация диэлектрика с энергией Е, — решение уравнения (4.40) для плотности тока j_x, можно за­писать так:

(4.41)

 

где n_e — концентрация электронов.

Вместо комплексной диэлектрической проницаемости ε^*, определяемой уравнением (4.36), можно ввести комплексную проводимость с помощью уравнения j_x=σ^*ε_x:

σ*=i ω ε_e^* ε₀= σ+iω ε_e ε₀                                                             (4.42)

где ε_e — электронная часть диэлектрической проницаемости. Поляризация атомов решетки дает вклад в диэлектричес­кую проницаемость, которую мы обозначим ε_L. Тогда ди­электрическая проницаемость будет равна

ε= ε_L+ ε_e

Рассмотрим предельный случай ω < τ> >>1. При длине волны λ =10 мкм / ω = 2*10¹⁴ рад*с^-1/ и при T=300 К ωτ_e»260, так что в ближней ИК-области это условие хорошо выполняется. В этом пределе, заменяя m_e на дрейфовую эф­фективную массу m_c, получим

                                                                                                       (4.43)

где

 

Используя формулу (4.5), можно получить выражение для коэффициента поглащения

α= σ₀ g (e²/ ω² m_c²)/(m_c² c ε₀ n)                               (4.44)

 

где n — показатель преломления.

Выражение (4.34) можно записать также в виде

где n_e, — концентрация электронов в зоне проводимости. Из­мерения поглощения на свободных носителях заряда, прове­денные на длинах волн за краем собственного поглощения, позволили проверить справедливость формулы (4.44) для многих полупроводников.

Оптические свойства полупроводников и фотоэлектриче­ские явления в объеме и на поверхности полупроводника привлекают всеобщее внимание по целому ряду причин, глав­ной из которых является открытие новых областей электро­ники и радиотехники — оптоэлектроники, функциональной электроники, квантовой электроники, — а также возможность непосредственного исследования структуры энергетических уровней, переходов между ними и т. д.

Рассмотрим падение пучка света на плоскую поверхность. Коэффициент пропорциональности а, представляющий собой количество поглощенной энергии из пучка единичной интен­сивности в слое единичной длины, называется коэффициентом поглощения:

dI =a Idx                                                                  (4.45)

После интегрирования выражения (4.45) получим

I=I₀e^-ax

Зависимость a= f (l) называется спектром поглощения.

В общем виде интенсивность отраженных и пропущенных материалом потоков, как это следует из рисунка 4.12, можно представить в виде выражений

 

 

 

где I — интенсивность прошедшего через образец луча, а Т— отраженного.

При поглощении света должны выполняться законы со­хранения энергии и импульса. Учитывая специфику данного курса, нас в первую очередь будут интересовать квантовые эффекты, вызванные переходами как внутри зон, так и между ними.

 

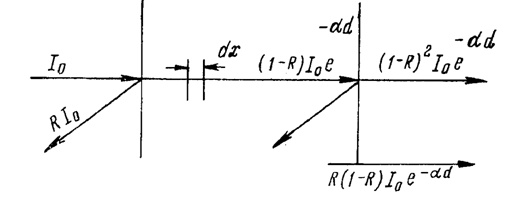
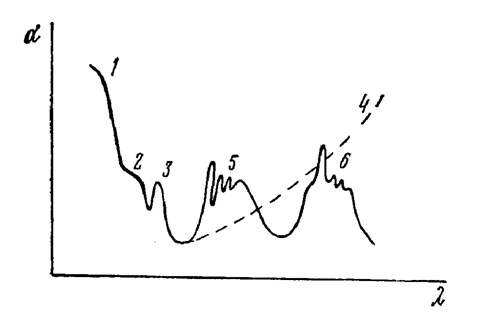
Рис. 4.12

Рис. 4.13

Различают собственное, экситонное, примесное, ре­шеточное поглощение света полупроводниками, а также пог­лощение света свободными носителями заряда в полупровод­никах. Общий вид спектра поглощения схематически пред­ставлен на рис. 4.13.

Собственное (основное, фундаментальное) поглощение света связано с переходом электронов из валентной зоны в зону проводимости. Закон сохранения энергии требует того, чтобы отсутствовало поглощение квантов света (по этому ме­ханизму) с энергией меньше ширины запрещенной зоны, т. е.

(hn)_погл ³ DЕ.

Определение ширины запрещенной зоны по краю фунда­ментального поглощения возможно лишь для очень чистых и совершенных кристаллических образцов. При изменении дли­ны волны света в коротковолновую сторону от края значе­ние коэффициентов поглощения достигает величины 10^-4 — 10^-5 см^-1. Различают прямые и непрямые переходы. Вероят­ность непрямых переходов много меньше, чем прямых. Эти переходы определяют поглощение, расположенное с длинно­волновой стороны у границы собственного поглощения. Как правило, энергию нельзя представить в виде функции одной переменной, за исключением специальных случаев, напри­мер, когда Е зависит лишь от величины вектора К. Обыч­но зависимость Е от К изображают графически для не­которых главных направлений в кристалле. Наглядно позна­комиться с прямыми и непрямыми переходами можно на примере рис. 4.14. Непрямой переход 5 можно представить

Рис. 4.14

в виде двух случаев. В одном случае электрон, находящийся вблизи потолка валентной зоны с К₁ = 0, возбуждаясь све­том, переходит в зону проводимости, занимая там состояния с тем же волновым вектором [1] (прямой переход). В ва­лентной зоне осталась дырка с К₁= 0. Однако электрон про­водимости с К₁=0 обладает большей энергией, чем та, ко­торая соответствует дну зоны проводимости, поэтому он че­рез очень малый промежуток времени совершает переход в состояние с минимальной энергией (К₂=К_min), испуская фонон (непрямой переход 2). В другом случае электрон воз­буждается излучением из глубоко лежащего состояния в ва­лентной зоне и совершает «вертикальный» переход в состоя­ние зоны проводимости, характеризуемое волновым векто­ром К= К_min (прямой переход 3 на рис. 4.14). В валентной зоне остается глубоко лежащая дырка, которая совершает переход в состояние вблизи потолка валентной зоны, где K=0, и одновременно испускает или поглощает фонон (не­прямой переход 4 на рис. 4.14). Материалы Si и Gе являются непрямыми полупроводниками, и у того, и у другого вершина валентной зоны расположена при K=0. В кремнии дно зоны проводимости расположено в направлениях <100> внутри зоны Бриллюэна (0,8 /K_max), и поэтому имеется шесть мини­мумов, в то время как в германии дно зоны проводимости расположено в направлениях <111> в точках на краю зо­ны Бриллюэна, поэтому здесь «имеется четыре минимума. Поверхности постоянной энергии и у того, и у другого мате­риала вблизи дна зоны проводимости имеют форму эллип­соидов вращения. У обоих полупроводников валентная зона при К=0 вырождена и имеет отщепленную зону, возникшую в результате спин-орбиталыюго взаимодействия. Из девяти двойных полупроводниковых соединений типа А^IIIB^V пять об­ладают «прямой» запрещенной зоной, а четыре—«непрямой». Величины минимальных значений ширин запрещенных зон DЕ (обозначены как «П» — прямая или «Н» — непрямая)

Таблица 4.3

АIIIBV	DЕ, эВ	mе/m0	mh1/m0	ml см2В-1c-1	mh см2В-1c-1
InSb	0,18	0,014	0,4	78000	750
InSn	0,35	0,022	0,4	28000	450
СаАs	0,72	0,044	0,23	44000	700
InР	1,33	0,078	-	5200	150
GаАs	1,42	0,065	0,5	8900	400
АlSb	1,62	-	-	200	-
А1Аs	2,13	-	-	-	-
GаР	2,26	-	-	200	100
АlР	2,43	-	-	-	-

приведены в табл. 4.3. Отметим высокую подвижность элек­тронов в InSb. При низких температурах она может превы­шать 10⁶ см²В^-1с^-1.

Собственное поглощение сильнолегированного полупровод­ника характеризуется сдвигом края в сторону коротких длин волн, как это показано на рис. 4.15 для вырожденного полу­проводника n-типа (уровень заполнения зоны проводимости показан пунктирной
линией). Рассматривая влияние внешних воздействий на собственное поглощение
полупроводника, необходимо отметить, что все те факторы, которые влияют на ширину запрещенной зоны: температура, давление, электрические и магнитные по­ля и т.д.,— влияют соответственно и на край фундаментального поглощения. Так, повышение температуры, вызывающее расширение решетки и усиление колеба­ний атомов относительно положения рав­новесия, вызывает уменьшение ширины запрещенной зовы и смещение фундаментального поглощения в сторону длинных волн.

Рис. 4.15

Из общих принципов квантовой механики можно пока­зать, что переходы могут вызываться поглощением не одного фотона, а двух и более, лишь бы суммарная энергия была достаточна для осуществления перехода. Вероятность про­цесса с участием нескольких фотонов резко уменьшается по мере увеличения числа последних. Поэтому практический ин­терес представляет лишь двухфотонное поглощение, которое можно наблюдать под действием лазерного излучения.

Экситонное поглощение наблюдается в процессах, когда электрон, поглотив квант света, не переходит в зону прово­димости, а образует с дыркой связанную систему, в которой электрон и дырка двигаются в одном и том же направлении. Импульс экситона связан с движением его центра масс. Его энергия строго дискретна:

E_ex=ħ²/(2M)*K_ex² - W_exⁿ

где W_exⁿ — энергия связи экситона в n-м возбужденном со­стоянии, а М=m_n+m_p. По сути дела экситон представляет собой возбужденное состояние атома в кристалле, передаю­щееся от атома к атому посредством квантомеханичеокого резонанса. В полупроводнике с прямыми переходами экситону соответствует пик поглощения 3 на краю фундаменталь­ного края полосы поглощения (рис. 4.13). В кремнии обнаружено четыре экснтонных подъема, связанных с поглоще­нием как оптических, так и акустических фононов.

При поглощении света полупроводниками возможно и та­кое возбуждение электронов и дырок, при котором кулоново взаимодействие между ними приводит к образованию ионоподобных или молекулоподобных комплексов. Например, два связанных электрона и одна связанная дырка могут об­разовать экситонный ион.

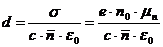Поглощение свободных носителей заряда вызывает пере­ходы носителей между состояниями в одной незаполненной зоне. Эти процессы осуществляются либо с генерацией, либо с поглощением фонона в том случае, когда происходит рас­сеяние на ионизированных примесях или дефектах. В послед­нем случае их можно рассматривать по механизму непрямых переходов. Коэффициент поглощения свободных носителей (пик 4, рис. 4.13) зависит от концентрации последних, их эффективной массы m*, среднего времени жизни τ и по­казателя преломления среды n:

 

Примесное поглощение (пик 5, рис. 4.13) происходит за счет ионизации или возбуждения светом примесных центров в кристалле. Отметим, что примесные центры могут харак­теризоваться наличием нескольких уровней возбуждения, что в свою очередь, приведет к появлению тонкой структуры в спектре примесного поглощения.

Решеточное поглощение наблюдается при возбуждении светом колебаний кристаллической решетки (пик 6, рис. 4.13). Интенсивность и положение полос слабо зависят от концент­рации дефектов примесей в полупроводнике. За счет энергии поглощенного фонона возникают дополнительные фононы.

е) Люминесценция полупроводников

Люминесценция является процессом, обратным поглоще­нию, т. е. случаем, когда полупроводник, находящийся в воз­бужденном состоянии, испускает электромагнитное излуче­ние.

Согласно принципу Франка—Кондона, спектр люминесцен­ции, как правило, смещен в сторону длинных волн по срав­нению с длиной волны возбуждения света.

Длительность спонтанного свечения определяется време­нем жизни носителей в возбужденном состоянии. В случае мономолекулярной релаксации возбужденных состояний I_Л ~ I₀e^-t/τ. При большом уровне возбуждения интенсивность люминесценции описывается выражением

I=I⁰/(1+βt)²

где β — константа, зависящая от степени предварительного возбуждения. В случае такой зависимости считают, что лю­минесценция идет по бимолекулярному механизму. По анало­гии с процессом поглощения рассмотрим рекомбинационное излучение полупроводников при фундаментальных перехо­дах, которое возникает при непосредственной рекомби­нации свободных носителей, при аннигиляции экситонов, а также при излучательной рекомбинации носителей через рекомбинационные ловушки, которые выступают в качестве центров свечения.

Прямые переходы наиболее вероятны. С ростом темпера­туры в незаполненных зонах заполняются все более высоко­лежащие состояния и в спектре люминесценции появляется коротковолновый «хвост».

В примесных полупроводниках люминесценция идет пре­имущественно через локализованные центры рекомбинации. Отметим, кто при рекомбинации донор — акцептор последние необходимо рассматривать как неподвижную молекулу, по­мещенную в кристалл:

hυ=ΔE-E_A-E_D+e²/ε²

т. е. кулоново взаимодействие между донором и акцептором, находящихся в среде с диэлектрической проницаемостью ε, вызывает уменьшение их энергии связи на величину

ΔE_кул= e²/ε²

В зависимости от узлов кристаллической решетки, которые занимают доноры и акцепторы, существуют различные виды активных центров. Для получения стимулированного излуче­ния в полупроводниках система должна находиться в состоя­нии с инверсной заселенностью. При этом

F_n-F_p> hυ

F_n-F_p> ΔE

где F_n и F_p, — положения квазиуровня Ферми для электронов и дырок соответственно. В таком случае система прозрачна на длине волны излучения. Состояние с инверсной заселен­ностью в полупроводниках может быть создано инжекцией неосновных носителей через p-n переход за счет возбуж­дения материала электромагнитным излучением, облучением электронами высоких энергий, ударной ионизацией в силь­ном электрическом поле.

ж) Поверхностные явления в полупроводниковых материалах

Физическое состояние поверхности и ее влияние на элект­рофизические характеристики полупроводников особенно важны в микроэлектронике, где подавляющее большинство элементов — пленочное, т. е. состояния поверхности подчас превалируют над объемными. Сама поверхность кристал­ла—это нарушение периодичности, т. е. непрерывный ряд дефектов. Эти дефекты возникают, во-первых, из-за отрыва на поверхности химических связей (уровни Тамма) и, во-вторых, вследствие адсорбции различных примесей (кислоро­да, воды и т. д.) на поверхности полупроводника. Очевидно, реальная сложная структура поверхности характеризуется набором поверхностных состояний, т. е. дополнительными энергетическими уровнями в запрещенной зоне донорного и акцепторного типа или ловушек.

Суммируя вышесказанное, выделим основные четыре при­чины, из-за которых наличие границы раздела приводит к видоизменению физических явлений в конденсированных сре­дах и к возможности их практического использования в ра­диотехнических системах:

1) в приповерхностном слое определенной толщины могут быть локализованы поверхностные электронные состояния и квазичастицы, свойства которых существенно отличаются от объемных;

2) сами объемные характеристики вещества изменяются по мере того, как размер кристалла в одном из направлений становится сравнимым с одной из характеристических длин: длиной свободного пробега, длиной экранирования, длиной волны электрона и т.д.;

3) на границе двух фаз имеет место их специфическое взаимодействие и влияние одной фазы на другую, например туннелирование электронов из полупроводника в оксид: гибридизация — взаимодействие и обмен электронами между металлом и полупроводником и т. д.;

4) приповерхностные области полупроводника являются, как правило, областями сильных электрических полей, вели­чинами которых можно управлять при создании ряда мик­роэлектронных и оптоэлектронных систем.

При комнатной температуре большинство примесей адсор­бируется на поверхности в виде ионов. Для компенсации их зарядов в поверхностном слое полупроводника образуется объемный заряд. Рассмотрим случай, когда на поверхности полупроводника n-типа имеется небольшое количество отри­цательно заряженных поверхностных состояний (рис. 4.16).

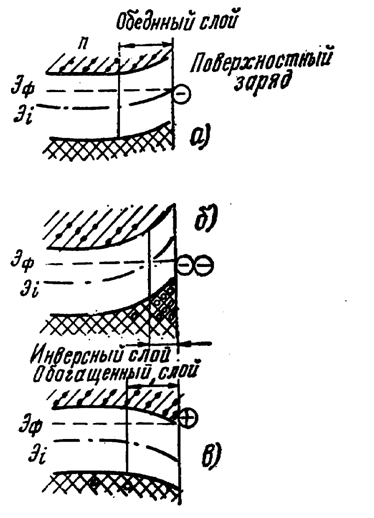
Рис. 4.16

В этом случае электростатическое поле поверхностных заря­дов проникает в полупроводник, создавая там обедненный слой, толщина которого определяется удельным сопротивле­нием материала. При большой плотности отрицательных по­верхностных зарядов у поверхности образуется инверсионный слой — с противоположным типом проводимости. Глубину залегания такого слоя опреде­ляют в точке пересечения уровня Ферми с серединой запрещенной зоны. Под инверсионным слоем находится обедненный слой, как и в выше разобранном случае. В случае на­личия на поверхности полу­проводника n-типа положительных поверхностных зарядов образуется обогащенный слой, глубина которого определяется проникновением электрического поля положительных зарядов в объем полупроводника. На практике мы обычно встречаемся c ситуацией, когда поверхность по­крыта оксидным слоем. В этом случае поверхностные состоя­ния могут существовать также в объеме оксида или на его поверхности. При этом разли­чают быстрые поверхностные состояния, располагающиеся на поверхности полупроводника и релаксирующие в тече­ние 10^-4—10^-8 с в случае перезарядки их электрическим полем, и медленные, расположенные в глубине оксида, переза­рядка которых занимает значительно большее время.

Быстрые поверхностные состояния могут выступать в ка­честве рекомбинационных ловушек, значительно изменяя вре­мя жизни носителей заряда всей системы τ_эфф:

1/ τ_эфф=1/ τ_υ + 1/ τ_s

где τ_υ, — время жизни в объеме полупроводника; τ_s — время жизни на поверхности полупроводника.

Плотность поверхностных состояний зависит как от обра­ботки поверхности, так и от свойств внешней среды, с кото­рой она соприкасается.

Кроме того, плотность поверхностных состояний может изменяться со временем из-за испарения или конденсации влаги на поверхности кристалла, из-за возможных миграций примесей по поверхности и к поверхности и т. д. Эти про­цессы приводят к изменению τ_эфф и могут являться причиной нестабильности параметров и характеристик полупроводни­ковых приборов и схем. К этим же результатам может при­водить и облучение, поглощающееся вблизи поверхности.

При проектировании радиоаппаратуры необходимо:

1. Выбрать метод обработки поверхности кристалла, при котором скорость поверхностной рекомбинации была бы ми­нимальна.

2. Разработать технологию длительного сохранения дос­тигнутых значений скорости поверхностной рекомбинации (покрытие, корпус, герметизация).

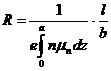Это тем более важно, что поверхностные состояния могут существенно изменять электрофизические свойства системы. Так, инверсионный слой может осуществлять электрическую связь между различными областями в микроэлектронных схе­мах, т. е. реализовать канал поверхностной проводимости. Сопротивление такого канала можно определить по формуле

где а—глубина канала; b и l--ширина и длина слоя, при­чем концентрация n и подвижность μ_n меняются по глубине. В этой связи часто пользуются параметром удельного сопро­тивления слоя ρ_s, — сопротивление квадрата этого слоя току, проходящему между двумя противоположными сторонами квадрата:

R= ρ_s*l/b

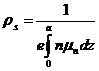где