6.1 Правила постановки размеров
Независимо от масштаба чертежа о предмете, изображенном на нем судят по размерным числам. Для нанесения размеров проводят выносные линии, ставят засечки, если речь идет о линейных размерах (для арх. Чертежей), или стрелки для радиусов и указываем разменные числа. Правила нанесения размеров на чертежах установлены ГОСТ 2.307 – 68*.
При нанесении размера отрезка размерная линия чертится параллельно ему, а выносные линии перпендикулярно (рис 5). Минимальный размер цифр на чертеже 3,5 мм (высота).
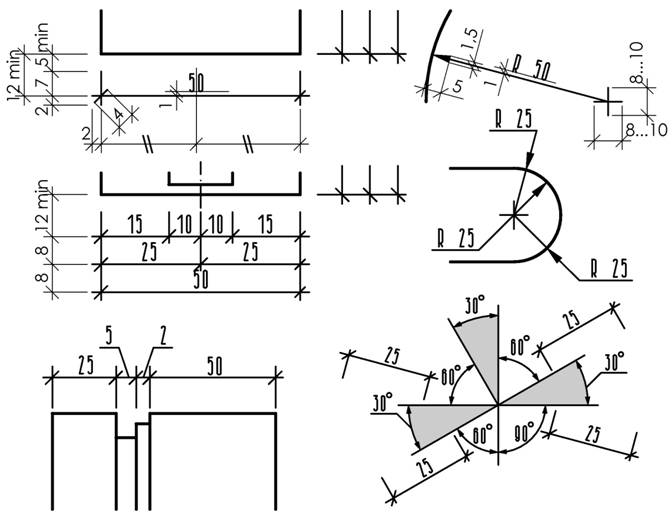
Рисунок 5.
Размерные числа наносятся над размерной линией, а размерные линии проводятся тонкими сплошными линиями (S/3) между выносными. Минимальное расстояние между параллельными размерными линиями должно быть 8 мм, а между размерной и линией контура – 12 мм.
Размерные числа располагают над размерной линией на расстоянии 1 мм, предполагая, что чертеж читается с правого нижнего угла (рис. 6,7).

Рис. 6. Простановка размеров

Рис. 7. Простановка размеров на плане
6.2 Архитектурный шрифт
Для выполнения любых надписей и подписей на чертеже используются стандартные шрифты, установленные ГОСТом (ГОСТ 2.304 – 81*). Они имеют следующие размеры – высоты (ширина определяется конкретным шрифтом): 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Для оформления архитектурных чертежей, чаще всего, применяется шрифт «архитектурный узкий», имеющий пропорции (отношение ширины к высоте) 1/5 или 1/6 (в нашем случае только 1/5). Для простоты работы со шрифтом примем модуль S, равный ширине буквы, тогда высота буквы будет равна 5S, расстояние между буквами – 1,5S, между словами - 5S (рис 8).

Рисунок 8. Архитектурный узкий шрифт.
Масштабы чертежей
Масштабы чертежей. Масштаб – отношение линейных размеров изображенного на чертеже объекта к его истинным размерам в натуре. Масштаб может быть выражен числом и тогда он называется – числовой масштаб или изображен графически – линейный масштаб. Знание числовой величины или размерности масштаба необходимо не только для выполнения чертежей в определенном масштабе, т.е. определенной величины, но и для проведения в дальнейшем измерений различных длин на готовых чертежах с тем, чтобы определить их натуральную (истинную) величину. Чертеж, выполненный в ортогональных проекциях в определенном масштабе, является документом по которому, как правило, выполняется изображенный на нем объект в натуре. Масштабы изображения на чертеже могут быть с уменьшением, увеличением и в натуральную величину. В числовом масштабе кратность увеличения или уменьшения обозначается дробью, и записывается так, как показано на рис.9, где изображена стандартная линейка числовых масштабов, рекомендованных ГОСТом.

Рисунок 9. Кратность масштабов.
Более полные данные о масштабах всегда можно найти в соответствующих справочниках. Чтобы определить масштаб изображения объекта на чертеже, необходимо взять какой-либо размер в натуре (обычно габаритный) и разделить его на длину этого размера на чертеже. Величина полученной дроби покажет число- вой масштаб, который не всегда будет соответствовать стандартной линейке масштабов. Если необходимо вычерчивать изображение на чертеже в стандартном масштабе, то подбирают ближайшее по величине его значение.
Можно строить изображение и в произвольном масштабе, но во всех случаях необходимо определить числовое значение основания масштаба.

Рисунок 10. Масштабные линейки.
Основание масштаба – величина, получаемая делением принятой единицы измерения (1м =1000 мм) на размер уменьшения. Например, для масштаба 1:25, величина основания масштаба составит: 1000:25 = 40 мм. Это значит, что основание масштаба будет изображаться отрезком длиной 40 мм и в двадцать пятом масштабе соответствовать 1 метру в натуре. Можно получить более мелкие значения измеряемых в данном масштабе величин, если разделить его основание на части, каждая из которых будет соответствовать целому числу.
Зная величину основания масштаба, легко построить линейный масштаб или масштабную линейку. Рис. 10. В свободном поле чертежа (обычно в нижней части листа) проводят прямую линию и на ней откладывают последовательно несколько раз основание масштаба. Длина получающейся линии произвольна и зависит в основном от композиционных задач. Левый отрезок делят вертикальными штрихами на части (обычно 10 частей) и над штрихом последнего деления справа ставят нуль. Отрезки справа, также разделенные короткими вертикальными штрихами, надписывают в цифровых значениях единицы измерения. Чаще всего в миллиметрах, как рекомендовано ГОСТом. Чертежи на подготовительных курсах и вступительном экзамене по черчению выполняются в масштабе 1:1 (один к одному), то есть в натуральную величину. Снабжаются надписью «МАСШТАБ 1:1» и строчкой линейного масштаба, которая может быть любой длины, в зависимости от композиции чертежа, но не менее длины основания масштаба, которая в данном случае равна 10 мм.
Для построения линейного масштаба проводят две горизонтальные линии на расстоянии 1–1,5 мм. Верхняя – 0,1 мм, нижняя толще в 3 – 4 раза (0,3 – 0,4 мм). На них откладывают по горизонтали ряд отрезков по 10 мм, обозначая их вертикальными штрихами высотой 3 – 5 мм. Первый отрезок с левой стороны делят на несколько равных частей более короткими вертикальными штрихами так, чтобы каждое деление соответствовало целому числу. Если этот отрезок разделить на 2 части, то каждое деление будет соответствовать 5мм, если на 5 частей – 2 мм, если на 10 – 1 мм. Последнее решение предпочтительней для достижения практически необходимой точности линейного масштаба. Над точками деления линий на отрезки, равные основанию масштаба, надписывают числовые значения, которые соответствуют натуральным размерам в миллиметрах, при этом у первого деления справа всегда ставят нуль.
Если числовые значения необходимо указать не в миллиметрах, а в других единицах измерения (сантиметрах, метрах и т.д.), то соответствующие размерные числа записывают с обозначением единицы измерения – см. или м. и т.д. Такое построение линейного масштаба очень удобно, так как позволяет вправо от нулевой отметки легко откладывать десятки, а влево единицы измерения для отрезков любой длины, не деля каждую секцию основания масштаба на более мелкие части, а только левую долю. В этом случае деление правых долей на мелкие доли теряет смысл, а точность отсчета цифровых значений длин измеряемых отрезков увеличивается за счет освобождения строки линейного масштаба от лишних членений.

Рисунок 11. Виды линейных масштабов.
Не следует делать вертикальные штрихи линейного масштаба слишком длинными, превращая его в «забор», и относить от них цифровые обозначения более чем на 1 – 2 мм, так как это снижает точность отсчета измеряемых величин. Чем длиннее штрихи, тем больше вероятность ошибки за счет не параллельности откладываемой величины горизонтальной линии масштаба.
Кроме того, линейный масштаб, имеющий большой размер в высоту и композиционно являющийся второстепенным, если не третьестепенным композиционным и смысловым элементом чертежа, может вступить в композиционное противоречие (противостояние) с более важными элементами композиции.
Например: он может оказаться по высоте значительно больше букв заголовка, и занять по отношению к нему главенствующую роль, что вряд ли можно признать удачным. Отдельные цифры и группы цифр должны располагаться строго симметрично над штрихами линейного масштаба. Это требование связано с необходимостью, уменьшить погрешность отсчета измеряемых по масштабу величин.
Наибольшую точность измерений на чертежах обеспечивает поперечный масштаб, который позволяет выразить или, определить размер с погрешностью до сотых долей основной единицы измерения. Рис. 11. Если в качестве единицы масштаба используется модуль, то такой масштаб называется модульным масштабом. Рис. 8. В некоторых случаях при вычерчивании чертежей бывает удобно использовать угловой или пропорциональный масштаб, особенно тогда, когда кратность увеличения или уменьшения изображения отличается от рекомендованных стандартом величин. Не забывайте, что на увеличенном чертеже, как и на заданном, необходимо проставлять числами действительные размеры изображаемого объекта, а не те, которые получились на чертеже.
Литература
1. Бархин Б.Г. Методика архитектурного проектирования. Спец. «Архитектура». – М.: Стройиздат, 1993. – 224 с.
2. Вяткин Г.П., Андреева А.Н., Болтухин А.К. и др. / Под ред. Г.П.Вяткина / Машиностроительное черчение. – М.: Просвещение, 1977. – 304 с.
3. Зайцев К. Современная архитектурная графика. – М.: Стройиздат, 1970. – 203 с.
4. Под ред. А.В. Степанова и М.А. Туркуса. Объемно-пространственная композиция в архитектуре. – М.: Стройиздат, 1975. –192 с.
5. Зайцев К.Г. Современная архитектурная графика. – М.: Стройиздат, 1970.
6. Кринский В.Ф., Колбин В.С., Ламцов И.В. и др. Введение в архитектурное проектирование. – М.: Госстройиздат, 1962.
7. Кудряшов К.В. Архитектурная графика. – М.: Стройиздат, 1990. – 312 стр.
8. Тиц А.А. и др. Основы архитектурной композиции и проектирования. – Киев: Высшая школа, 1976. – 256 стр.
Приложение А.
Пример выполнения курсовой работы.

Автор – Ковалькова И.В.
Приложение Б.
Пример выполнения курсовой работы.

Автор – Арутюнова С.К.
Приложение В.
Пример выполнения курсовой работы.

Автор – Немтинова Т.А.
Приложение Г.
Пример выполнения курсовой работы.
Автор – Стрелкова Т.Н.






