Введение
Теория алгоритмов – это раздел математики, изучающий теоретические возможности эффективных процедур вычисления и их приложения.
Теория ЭВМ, теория и практика программирования не могут без нее обойтись. Кибернетика и математическая логика рассматривают теорию алгоритмов как один из своих разделов. Например, алгоритм можно рассматривать как математическую модель программы. Однако теория алгоритмов является самостоятельной наукой и имеет собственный предмет исследования.
Само название теории говорит о том, что ее предмет – алгоритмы. Понятие алгоритма является и очень простым, и очень сложным. Его простота состоит в многочисленности алгоритмов, с которыми мы встречаемся повсюду, в их обыденности. Но эти же обстоятельства делают понятие алгоритма туманным, расплывчатым, трудно поддающимся научному определению.
Точное понятие "алгоритм" было выработано лишь в тридцатых годах XX века. До этого математики довольствовались интуитивным понятием алгоритма. Это объясняется тем, что до середины XIX века математика имела дело в основном с числами и вычислениями. Понятие алгоритма отождествлялось с понятием метода вычислений. Все многообразие вычислений комбинировалось из четко определенных операций арифметики, тригонометрии и анализа. Поэтому понятие метода вычисления считалось интуитивно ясным и не нуждалось в специальных исследованиях.
Новые более жесткие требования к строгости стимулировались в основном математикой нечисловых объектов во второй половине XIX века. Одним из решающих обстоятельств, приведших к пересмотру оснований математики, явилось создание Кантором теории множеств.
Опыт парадоксов теории множеств научил математику крайне осторожно обращаться с бесконечностью и даже о бесконечности рассуждать с помощью финитных методов. Существо финитного подхода заключается в том, что он допускает только конечные комплексы действий над конечным числом объектов. Выяснение того, какие объекты и действия над ними следует считать точно определенными, какими свойствами и возможностями обладают комбинации элементарных действий, что можно и чего нельзя сделать с их помощью - все это стало предметом теории алгоритмов. Главным внутриматематическим приложением теории алгоритмов явились доказательства невозможности алгоритмического решения некоторых математических проблем. Такие доказательства неосуществимы без точного понятия алгоритма (для доказательства несуществования алгоритма решения того или иного класса задач, надо точно знать несуществование чего требуется доказать).
1. Интуитивное понятие алгоритма
Человек ежедневно встречается с множеством задач, возникающих в различных областях деятельности общества, например:
а) подготовиться к уроку по математике;
б) приготовить раствор для проявления фотопленки;
в) избавиться от лишнего веса.
Для решения задач надо знать, что дано, и что следует получить. Другими словами, задача представляет собой совокупность двух объектов: исходных данных и искомых результатов. Чтобы получить результаты, необходимо знать метод решения задачи, то есть располагать предписанием (инструкцией, правилом), в котором указано, какие действия и в каком порядке следует выполнить, чтобы решить задачу (получить искомые результаты). Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, называется алгоритмом.
Алгоритм - это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения (после конечного числа шагов) искомого результата.
Следует иметь в виду, что это – не определение в математическом смысле слова, но довольно подробное описание понятия алгоритма, раскрывающее его сущность. Описание может быть другим. Так, в одном из школьных учебников по информатике понятие алгоритма дается в следующей форме: " Под алгоритмом понимают понятное и точное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи ". Математическая энциклопедия так определяет понятие алгоритма: «Алгоритм – это точное предписание, которое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного данного (из некоторой совокупности возможных для данного алгоритма данных) и направленный на получение полностью определяемого этим исходным данным результата.»
Еще на самых ранних ступенях развития математики в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам. К числу таких правил относились и правила выполнения арифметических операций над числами.
Столетия эти правила были очень сложны и не удивительно поэтому, что производить вычисления с большими числами могли только люди с высшим образованием. Так, чтобы научиться арифметическому делению в средние века требовалось закончить университет. Да еще не всякий университет мог научить этой премудрости. Нужно было непременно ехать в Италию: тамошние математики добились большого искусства в делении. Если напомнить, что в те времена пользовались непозиционной (римской) системой счисления, станет ясно, почему деление миллионных чисел было доступно лишь бородатым мужам, посвятившим этому всю свою жизнь.
С введением позиционной системы счисления все изменилось. В IX веке узбекский математик Абу-Джафар Мухаммед ибн Муса ал-Хорезми ("ал-Хорезми" означает "Хорезмиец") описал правила выполнения четырех арифметических действий в десятичной системе счисления. Новые правила были значительно проще и сейчас ими владеют уже школьники младших классов. Поразительная простота указанных правил стимулировала их повсеместное распространение. Эти правила были изложены Мухаммедом в книге по математике «Китаб аль-джебр валь-мукабалла» (Книга о восстановлении и противопоставлении), изданной в 825 году. В ней, кроме того, приводились многочисленные рецепты решения различных задач.
Книга была переведена на латинский язык в XII в. и оказала большое влияние на развитие математики в Западной Европе. По латинским переложениям арифметического трактата ал-Хорезми средневековая Европа знакомилась с индийской позиционной системой счисления и с искусством счета в этой системе. При переводе имя автора переделали в Алгоритми. Ссылки на рецепты решений из книги Мухаммеда европейские авторы начинали со слов: "Так говорил Алгоритми...". С течением времени сами рецепты для решения математических задач стали называть алгоритмами.
Первоначально под алгоритмами понимали только правила выполнения четырех арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.
Для разъяснения интуитивного понятия алгоритма рассмотрим несколько примеров.
В качестве первого примера рассмотрим один из самых древних и самых известных математических алгоритмов - алгоритм нахождения наибольшего общего делителя двух натуральных чисел. Этот алгоритм еще в III веке до нашей эры изложил (в геометрической форме) греческий ученый Евклид в теоретическом трактате по математике "Начала". Поэтому он носит название алгоритма Евклида. Алгоритм Евклида обсуждается практически в каждой книге по программированию.
Пример 1.1. Вычисление наибольшего общего делителя двух натуральных чисел m и n.
Составим алгоритм решения этой задачи в предположении, что его исполнителем будет некоторое вычислительное устройство.
Алгоритм Евклида
1. Поместить в участок памяти с именем x число m; перейти к выполнению пункта 2.
2. Поместить в участок памяти с именем y число n; перейти к выполнению пункта 3.
З. Если выполняется условие 
, то перейти к выполнению пункта 5, иначе перейти к выполнению пункта 4.
4. Поместить в участок памяти с именем НОД значение из блока памяти x; перейти к выполнению пункта 8.
5. Если выполняется условие x > y, то перейти к выполнению пункта 6, иначе перейти к выполнению пункта 7;
6. Поместить в участок памяти с именем x значение выражения x - y; перейти к выполнению пункта 3.
7. Поместить в участок памяти с именем y значение выражения y - x; перейти к выполнению пункта 3.
8. Закончить работу.
Внимательное рассмотрение алгоритма Евклида показывает, что запись алгоритма распадается на отдельные команды. Каждая команда снабжена номером и представляет собой указание исполнителю выполнить некоторое законченное действие. Исполнение алгоритма начинается с команды, имеющей номер 1. Далее команды выполняются в соответствии с указаниями, сопровождающими каждую команду алгоритма.
Для удобства ссылок, алгоритм обычно снабжается названием. В случае, когда для алгоритма не указывается специальное название, его названием обычно считают весь текст задачи, для решения которой этот алгоритм предназначен.
Существует правило, согласно которому, при отсутствии специального указания следующей за данной командой должна выполняться команда, номер которой на единицу больше данной. Такая последовательность выполнения команд называется естественной. По указанию "кончить работу" исполнение алгоритма прекращается.
Пример 1.2. Умножение натуральных чисел столбиком.
1. Записать множимое.
2. Подписать множитель под множимым так, чтобы разряды множителя находились под соответствующими разрядами множимого.
3. Провести черту под множителем (под ней будут записываться частные суммы).
4. Взять очередную цифру множителя, начиная с единиц.
5. Если очередная цифра множителя равна нулю, пропустить ее и перейти к пункту 7.
6. Если очередная цифра не равна нулю, умножить на нее множимое и произведение как очередную частную сумму, подписать под чертой или под предыдущей частной суммой так, чтобы единицы произведения находились бы под очередной цифрой множителя.
7. Если очередная цифра не была последней, перейти к пункту 4.
8. Если очередная цифра оказалась последней, сложить частные суммы столбиком и общую сумму взять в качестве искомого произведения.
Пример 1.3. Инструкция по приготовлению проявителя. Содержимое большого пакета растворить в 300 мл. воды при температуре I8-20° C; затем добавить содержимое малого пакета. Объем раствора довести до 500 мл. Раствор профильтровать.
В этом примере команды не пронумерованы. Все команды записаны последовательно, в виде сплошного текста. Друг от друга команды разделены либо точкой, либо точкой с запятой. При таком оформлении алгоритма исполнитель выполняет команды в порядке их естественного следования в тексте.
Такая форма записи алгоритма часто используется во всякого рода инструкциях, правилах, рецептах и т.п. Она хороша в случае, когда алгоритм небольшой и когда для описания алгоритма отводится мало места. Недостатком такого оформления является его малая наглядность.
2. Свойства алгоритмов
Профессор Стенфордского университета Д.Кнут в книге «Искусство программирования для ЭВМ» отмечает, что современное значение слова «алгоритм» очень сходно со значением слов «рецепт», «процесс», «метод», «способ», «процедура», «программа», но имеет свой дополнительный смысловой оттенок. Это уточнение смысла может быть сформулировано как перечень некоторых свойств, которыми должен обладать любой алгоритм.
Перечислим те свойства, важность которых признается всеми учеными. Это: дискретность, элементарность шагов, определенность, результативность, конечность и массовость.
Рассмотренные примеры показывают, что выполнение алгоритма разбивается на последовательность законченных действий-шагов. Каждое действие должно быть закончено исполнителем прежде, чем он приступит к исполнению следующего действия. Это свойство алгоритма называется дискретностью. Таким образом, дискретность означает, что алгоритм состоит из конечного числа описаний шагов и эти шаги выполняются в дискретном времени, то есть любые два последних шага разделены при исполнении конечным, ненулевым отрезком времени. Можно считать, что шаги выполняются в моменты времени t0, t1,…, а между этими моментами ничего не происходит.
Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой.
Элементарность шагов означает, что объем работы, выполняемой на любом шаге, определяется некоторой константой, зависящей от входных данных и промежуточных значений, получаемых алгоритмом, а также от исполнителя. Понятно, что элементарность шагов для исполнителя-человека и исполнителя-ЭВМ не будет одинаковой. Для численных алгоритмов такими шагами могут быть, например, сложение, вычитание, умножение, деление, сравнение двух чисел, пересылка одного числа из некоторого места памяти в другое. Но к элементарным шагам не относится, например, сравнение двух файлов, так как время сравнения зависит от длины файлов, а длина потенциально неограниченна.
Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было известно, какую команду надо выполнить следующей. Это свойство алгоритма называется точностью.
Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может ее исполнить в строгом соответствии с ее назначением. Это свойство называется понятностью (для данного исполнителя).
- Да пойми же, гайками прикрепляется рельса к шпалам!
- Это мы понимаем...
А.Чехов "Злоумышленник"
Будучи понятным, алгоритм не должен все же содержать предписаний, смысл которых может восприниматься неоднозначно. Это означает, что одно и то же предписание после исполнения должно давать один и тот же результат.
В данном случае речь фактически идет о том, что запись алгоритма должна быть настолько четкой, настолько полной и продуманной в деталях, чтобы у исполнителя никогда не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места, для произвола исполнителя.
Отмеченное свойство называется свойством определенности, или детерминированности.
Замечание. Часто под свойством детерминированности алгоритма понимается одновременное выполнение свойств точности и понятности.
Важным свойством алгоритма является свойство результативности. Смысл этого свойства состоит в том, что при точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет. В частности, если вычисляемая функция в данном шаге не определена, совокупность правил должна определять, что в этом случае следует считать результатом применения алгоритма.
Конечность (финитность) алгоритма означает, что для получения результата нужно выполнить конечное число шагов, то есть исполнитель в некоторый момент времени останавливается. Требуемое число шагов зависит отвходных данных алгоритма и не определяется константой.
Считается, что алгоритм наиболее интересен, если он, кроме того, обладает свойством массовости, т.е. пригодности для решения любой задачи из некоторого класса задач. Это свойство не следует понимать как возможность решить много задач. Свойство массовости предполагает, что заданный алгоритм позволяет решить любую задачу из определенного класса, причем этот класс может состоять и только из одной задачи.
Проиллюстрируем свойства алгоритма на примере алгоритма Евклида.
Массовость алгоритма Евклида заключается в том, что его можно применить к любой паре натуральных чисел. Результативность его состоит в том, что он определяет процесс, приводящий для любой пары натуральных чисел к получению их наибольшего делителя. Понятность алгоритма заключается в том, что исполнитель умеет выполнять действия, определяемые командами алгоритма. Детерминированность алгоритма вытекает из того, что каждая команда выполняется исполнителем однозначно. Точность алгоритма обеспечивается тем, что, во-первых, исполнителю известно, с чего начинать выполнение алгоритма (с команды номер 1), и, во-вторых, каждая команда снабжена указанием, какую команду выполнять следующей.
Рис.2.1. Непонятное предписание
Очевидно, не каждое правило, приводящее к решению задачи, является алгоритмом. Разберем с этих позиций несколько таких правил.
Пример 2.1. Проведение перпендикуляра к прямой MN в заданной точке A.
1. Отложить в обе стороны от точки A на прямой MN циркулем отрезки равной длины с концами B и C,
2. Увеличить раствор циркуля до радиуса, в полтора-два раза большего длины отрезков AB в AC.
3. Провести указанным раствором циркуля последовательно с центрами B и C дуги окружностей так, чтобы они охватили точку A и образовали две точки пересечения друг с другом D и E.
4. Взять линейку и приложить ее к точкам D и E и соединить их отрезком. При правильном построении отрезок пройдет через точку А и будет искомым перпендикуляром.
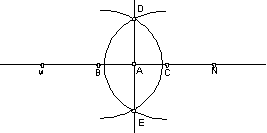
Рис. 2.2. Проведение перпендикуляра к прямой в заданной точке
Указанное правило, очевидно, рассчитано на исполнителя-человека. Применяя его, человек, разумеется, построит искомый перпендикуляр. Но, тем не менее, это правило алгоритмом не является.
Прежде всего, оно не обладает свойством детерминированности. Так, в пункте 1 требуется от исполнителя сделать выбор отрезка произвольной длины (для построения точек B и C надо провести окружность произвольного радиуса r с центром в точке A). В пункте 2 требуется сделать выбор отрезка в полтора-два раза большего длины отрезков AB и AC. В пункте 3 надо провести дуги, которые также однозначно не определяются их описанием. Человек-исполнитель, применяющий данное правило, к одним и тем же исходным данным (прямой MN и точке A) повторно, получит несовпадающие промежуточные результаты. Это противоречит требованию детерминированности алгоритма.
Попробуем переформулировать это правило, чтобы оно стало алгоритмом. Для этого следует во всех предписаниях избавить исполнителя от проблемы выбора. Вместо выбора произвольного радиуса будем указывать в каждом случае конкретный. Однако этим неопределенность команд полностью не снимается. В инструкциях 1 и 2, кроме проведения окружностей, требуется находить точки пересечения и как-то их обозначать. Разберем возникающие при этом проблемы.
В команде 2 требуется присвоить имена точкам пересечения прямой MN и окружности 
. Здесь можно договориться обозначать точки, например, так, чтобы векторы 
и 
были сонаправлены.
В команде 3 требуется обозначить точки пересечения окружносте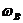й 
и 
. Договоримся, например, обозначать через D ту из двух точек пересечения, которая находится левее, если смотреть из центра B в направлении центра C.
Кроме того, вместо дуг окружностей в пункте 3, мы будем проводить окружности, ибо тем самым снимается неопределенность инструкции "провести дугу, охватывающую точку".
С учетом сказанного искомый алгоритм может выглядеть следующим образом.
Пример 2.2. Алгоритм проведения перпендикуляра к прямой MN в заданной точке A (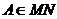
).
1. Провести окружность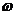 
радиуса 1 с центром в точке A.
2. Обозначить точки пересечения окружности 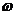с прямой MN через B и C так, чтобы 
.
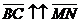3. Последовательно провести окружност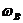и и радиуса 2 с центром соответственно в точках B и C.
4. Обозначить точки пересечения окружносте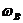й и через D и E так, чтобы обход многоугольника BDCE (последовательно от B через D и C к E) совершался по часовой стрелке.
5. Провести прямую DE. Прямая DE - искомый перпендикуляр.
Рис.2.3. Проведение перпендикуляра к прямой в заданной точке
В школьном учебнике [6] приведен алгоритм нахождения середины отрезка при помощи циркуля и линейки. В нем использован другой прием избавления от неопределенности инструкций при геометрических построениях.
Замечание. Подробное обсуждение вопросов, связанных с алгоритмами построения циркулем и линейкой, проводится в книге Абрамова С. А. «Математические построения и программирование». Всем, изучающим информатику, полезно познакомиться с этой интересной книгой.
3. Уточнение понятия алгоритма
"То, что вообще может быть сказано, может быть сказано ясно, а о чем невозможно говорить - о том следует молчать".
Людвиг Витгенштейн (Эпиграф, предпосланный изложению языка программирования АЛГОЛ-60.)
Точное математическое определение понятия "алгоритм" было выработано лишь в тридцатых годах XX века. Почему же до этого времени математики довольствовались интуитивным понятием алгоритма? Это связано с тем, что обычно понятие алгоритма встречалось в связи с конкретным решением задачи. Об алгоритме говорили лишь тогда, когда предлагался способ решения какого-либо класса задач. В начале XX века в математике накопилось большое количество задач, которые не поддавались решению, несмотря на то, что над ними думали первоклассные ученые. Возникло подозрение, что для некоторых из этих задач вообще не существует разрешающего алгоритма. Утверждение о неразрешимости того или иного класса задач можно было вывести, только имея точное определение алгоритма, надо было знать, несуществование чего требуется доказать.
Попытки дать строгое математическое определение алгоритма, согласующееся с интуитивным представлением об алгоритме, привели к выработке сразу нескольких определений (Черч, Пост, Тьюринг, Марков и др.). Впоследствии выяснилось, что все эти определения равносильны между собой и, следовательно, определяют одно и то же понятие. В качестве основы для уточнения понятия алгоритма мы выбираем так называемые машины с неограниченными регистрами, или, короче, МНР. Изложение на базе МНР привлекательно ввиду близости этих машин к реальным ЭВМ.
Каждый алгоритм имеет дело с данными - входными, промежуточными и выходными. Поскольку мы собираемся уточнять понятие алгоритма, нужно уточнить и понятие данных. В качестве данных для МНР мы ограничиваемся множеством Z0 неотрицательных целых чисел. Такое ограничение не является существенным, поскольку другие виды объектов и операции над ними могут быть закодированы натуральными числами и представлены как операции над натуральными числами.
Ниже мы перечислим все команды из списка предписаний МНР (для уточнения свойства "понятность"), однозначно определим действие каждой команды (для уточнения свойства "определенность") и опишем механизм реализации алгоритма (для уточнения свойства "точность").
Машина с неограниченными регистрами является исполнителем, представляющим собой простой "идеализированный компьютер". Идеализация состоит в том, что каждый отдельный реальный компьютер ограничен как величиной чисел, которые поступают на вход, так и размером памяти (необходимой для запоминания промежуточных результатов), МНР лишена этих ограничений. Машина с неограниченными регистрами имеет неограниченно большую память, ячейки которой будем называть регистрами и обозначать R1, R2, R3,…. Каждый регистр в любой момент времени содержит неотрицательное целое число.
| 
| 
| 
| ... |
| 
| 
| 
| ... |
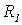
Рис. 3.1. Регистры МНР
При этом только конечное множество регистров содержит числа, отличные от нуля. Все остальные регистры заполнены нулями. Это допущение предполагает, что каждый алгоритм использует только конечный объем памяти.
В список предписаний МНР входит четыре команды: команда обнуления Z(n); команда прибавления единицы S(n); команда переадресации T(m, n) и команда условного переходам J(m, n, q). Команды обнуления, прибавления единицы и переадресации называются арифметическими.
| Обозначение команды | Действие, производимое МНР по данной команде |
| Z(n) | Rn: = 0 |
| S(n) | Rn: = Rn + 1 |
| T(m, n) | Rn: = Rm |
| J(m, n, q) | Если Rm = Rn, то перейти к вычислению команды алгоритма с номером q. |
Рис. 3.2. Список предписаний МНР
Алгоритмом называется конечная непустая последовательность команд из списка предписаний МНР, начинающаяся с команды с номером 1.
Производя вычисления по данному алгоритму, МНР изменяет содержимое регистров памяти в точном соответствии с командами алгоритма. Исходное состояние памяти, то есть последовательность чисел 
в регистрах R1, R2, R3,…. перед началом вычислений, называется начальной конфигурацией.
Предположим, что некоторый алгоритм P состоит из последовательности команд I1, I2,..., Is. МНР начинает вычисление с команды I1, затем выполняются команды I2, I3 и т. д. до тех пор, пока не встретится команда вида J(m, n, q). В этом случае МНР переходит к выполнению команды, предписанной J(m, n, q) и текущим содержанием регистров Rm и Rn.
МНР выполняет алгоритм P: I1, I2,..., Is до тех пор, пока это возможно. Вычисление останавливается тогда и только тогда, когда нет следующей команды, то есть когда МНР только что выполнила команду Ik и следующая команда в вычислении есть Iv, где v > s. Это может произойти одним из способов:
I) если Ik = Is (выполнена последняя команда в P) и Ik - арифметическая команда;
2) если Ik = J(m, n, q), Rm = Rn и q > s.
3) если Ik = J(m, n, q), Rm Rn и q = s.
В этом случае будем говорить, что вычисление остановилось после выполнения команды Ik, и заключительная конфигурации есть последовательность r1, r2, r3,... содержимого регистров на этом шаге.
Результатом применения алгоритма к некоторой начальной конфигурации будем считать число r1 из регистра R1 заключительной конфигурации.
Бывают, конечно, вычисления, которые никогда не заканчиваются. В случае, если вычислительный процесс не заканчивается получением результата, говорят, что алгоритм неприменим к начальной конфигурации.
Пример 3.1. Рассмотрим алгоритм P1
| I1 | J(1, 2, 6) |
| I2 | S(2) |
| I3 | S(3) |
| I4 | J(1, 2, 6) |
| I5 | J(1, 1, 2) |
| I6 | T(3, 1) |
Применим алгоритм к следующей начальной конфигурации:
| R1 | R2 | R3 | R4 | R5 | ... |
| 5 | 3 | 0 | 0 | 0 | ... |
Рис. 3.3. Начальная конфигурация
Ход вычисления на МНР по алгоритму P1 с начальной конфигурацией, изображенной на рисунке 3.3, можно представить, записывая последовательно сверху вниз конфигурации машины вместе со следующей командой, к которой она переходит на данном шаге.
| R1 | R2 | R3 | R4 | R5 | ... | Следующая команда | Комментарий | |
| 5 | 3 | 0 | 0 | 0 | ... | I1 | ||
| 5 | 3 | 0 | 0 | 0 | ... | I2 | (так как  )
| |
| 5 | 4 | 0 | 0 | 0 | ... | I3 | ||
| 5 | 4 | 1 | 0 | 0 | ... | I4 | ||
| 5 | 4 | 1 | 0 | 0 | ... | I5 | (так как )
| |
| 5 | 4 | 1 | 0 | 0 | ... | I2 | (так как  )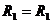
| |
| 5 | 5 | 1 | 0 | 0 | ... | I3 | ||
| 5 | 5 | 2 | 0 | 0 | ... | I4 | ||
| 5 | 5 | 2 | 0 | 0 | ... | I6 | (так как R1 = R2) | |
| 2 | 5 | 2 | 0 | 0 | ... | I7 |
Рис. 3.4. Вычисление по алгоритму P1
Определение 3.1. Пусть f - функция от n неотрицательных целыхпеременных со значениями во множестве Z0 неотрицательных целых чисел(функция 
). Функция f называется вычислимой на МНР (или МНР-вычислимой), если существует такой алгоритм P, что:
1) вычисление P (a1, a2,..., an) останавливается тогда и только тогда, когда (a1, a2,..., an) принадлежит области определения f;
2) если (a1, a2,..., an) принадлежит области определения f; то в заключительной конфигурации в регистре R1 находится целое число b такое, что f (a1, a2,..., an) = b.
С этого момента под термином вычислимое будем подразумевать МНР-вычислимое.
Рассмотрим теперь несколько простых примеров вычислимых функций.
Пример 3.2. Докажите МНР-вычислимость функции x + y.
Решение. Получим x + y, прибавляя y раз 1 к числу x. Начальной конфигурацией алгоритма служит x, y, 0, 0, 0,.... Типичной конфигурацией в процессе вычисления является
| R1 | R2 | R3 | R4 | R5 | ... |
| x + k | y | k | 0 | 0 | ... |
Определим алгоритм следующим образом:
| I1 | J(3, 2, 5) |
| I2 | S(1) |
| I3 | S(3) |
| I4 | J(1, 1, 1) |
Заданный алгоритм вычисляет функцию x + y.
Пример 3.3. Докажите МНР-вычислимость функции 
Решение. Составим алгоритм для начальной конфигурации x, 0, 0,.... Типичной конфигурацией в процессе вычисления является:
| R1 | R2 | R3 | R4 | R5 | ... |
| x | k | k + 1 | 0 | 0 | ... |
Следующий алгоритм МНР - вычисляет функцию.
| I1 | J(1, 2, 6) |
| I2 | S(2) |
| I3 | J(1, 2, 6) |
| I4 | S(3) |
| I5 | J(1, 1, 2) |
| I6 | T(3, 1) |
За последние пятьдесят лет было предложено много математических уточнений интуитивного понятия "алгоритм". Подход, основанный на МНР, является одним из них. Между этими подходами имеются большие различия, и в то же время все эти подходы эквивалентны между собой в том же смысле, что каждое уточнение алгоритма приводит к одному и тому же классу вычислимых функций.
Возникает теперь вопрос: насколько хорошо неформальное интуитивное понятие вычислимой функции отражено в различных формальных описаниях? Этот вопрос подвергался математиками серьезному обсуждению, в результате которого было высказано утверждение, известное под названием " тезис Черча ": каждая функция, вычислимая посредством процесса, алгоритмический характер которого интуитивно ясен, является вычислимой функцией. Применительно к нашему изложению этот тезис можно перефразировать следующим образом: всякая функция, для которой существует алгоритм (в интуитивном смысле) вычисления ее значений, является МНР-вычислимой функцией.
Сразу же заметим, что это утверждение не является теоремой, подлежащей математическому доказательству; оно имеет статус утверждения, принимаемого как постулат, справедливость которого подтверждается рядом свидетельств. Во-первых, таким свидетельством является то, что, как уже отмечалось, многие независимые уточнения интуитивного понятия вычислимой функции привели к одному и тому же классу функций. Во-вторых, никому не доводилось найти функцию, которую можно признать вычислимой в интуитивном смысле и которая не была бы МНР-вычислимой. Исходя из этих соображений и собственного опыта, большинство математиков приняли тезис Черча.
Далее рассмотрим основные формализации понятия алгоритма на примере машин Поста и Тьюринга, а также нормальных алгоритмов Маркова и теории рекурсивных функций Черча.
Машина Поста
Одной из фундаментальных статей, результаты которой лежат в основе современной теории алгоритмов является статья Эмиля Поста (Emil Post), «Финитные комбинаторные процессы, формулировка 1», опубликованная в 1936 году в сентябрьском номере «Журнала символической логики»
Пост рассматривает общую проблему, состоящую из множества конкретных проблем, при этом решение общей проблемы это такое решение, которое доставляет ответ для каждой конкретной проблемы.
Например, решение уравнения 3х + 9 = 0 – это одна из конкретных проблем, а решение уравнения ax + b = 0 – это общая проблема, тем самым алгоритм (сам термин «алгоритм» не используется Постом) должен быть универсальным, т.е. должен быть соотнесен с общей проблемой.
Основные понятия алгоритмического формализма Поста – это пространство символов (язык L) в котором задаётся конкретная проблема и получается ответ, и набор инструкций, т.е. операций в пространстве символов, задающих как сами операции, так и порядок выполнения инструкций.
| Постовское пространство символов – это бесконечная лента ячеек (ящиков): | ||||||||
| _ | V | _ | _ | V | V | V | _ | V |
Каждый ящик или ячейка могут быть помечены или не помечены.
Конкретная проблема задается «внешней силой» (термин Поста) пометкой конечного количества ячеек, при этом, очевидно, что любая конфигурация начинается и заканчивается помеченным ящиком. После применения к конкретной проблеме некоторого набора инструкций решение представляется так же в виде набора помеченных и непомеченных ящиков, распознаваемое той же внешней силой.
Пост предложил набор инструкций (элементарных операций), которые выполняет «работник», отметим, что в 1936 году не было еще ни одной электронной вычислительной машины. Этот набор инструкций является, очевидно, минимальным набором битовых операций:
1. пометить ящик, если он пуст;
2. стереть метку, если она есть;
3. переместиться влево на 1 ящик;
4. переместиться вправо на 1 ящик;
5. определить помечен ящик или нет, и по результату перейти на одну из двух указанных инструкций;
6. остановиться.
Отметим, что формулировка инструкций 1 и 2 включает защиту от неправильных ситуаций.
Программа представляет собой нумерованную последовательность инструкций, причем переходы в инструкции (5) производятся на указанные в ней номера других инструкций.
Программа (набор инструкций в терминах Поста) является одной и той же для всех конкретных проблем, поэтому соотнесена с общей проблемой – таким образом, Пост формулирует требование универсальности.
Далее Пост вводит следующие понятия:
o набор инструкций применим к общей проблеме, если для каждой конкретной проблемы не возникает коллизий в инструкциях (1) и (2), т.е. никогда программа не стирает метку в пустом ящике и не устанавливает метку в помеченном ящике;
o набор инструкций заканчивается (за конечное количество инструкций), если выполняется инструкция (6);
o набор инструкций задаёт финитный 1 – процесс, если набор применим, и заканчивается для каждой конкретной проблемы;
o финитный 1 – процесс для общей проблемы есть 1 – решение, если ответ для каждой конкретной проблемы правильный (это определяется внешней силой).
По Посту проблема задаётся внешней силой путем пометки конечного количества ящиков ленты. В более поздних работах по машине Поста принято считать, что машина работает в единичной системе счисления (0=V; 1=VV; 2=VVV; 3=VVVV), т.е. ноль представляется одним помеченным ящиком, а целое положительное число – помеченными ящиками в количестве на единицу больше его значения.
Поскольку множество конкретных проблем, составляющих общую проблему счетное, то можно установить взаимно однозначное соответствие (биективное отображение) между множеством положительных целых чисел N и множеством конкретных проблем.
Общая проблема называется по Посту 1-заданой, если существует такой финитный 1 – процесс, что, будучи, применим к n є N в качестве исходной конфигурации ящиков, он задает n-ую конкретную проблему в виде набора помеченных ящиков.
Если общая проблема 1 -задана и 1 -разрешима, то, соединяя наборы инструкций по заданию проблемы, и ее решению мы получаем ответ по номеру проблемы – это и есть в терминах статьи Поста формулировка 1.
Эмиль Пост завершает свою статью следующей фразой: «Автор ожидает, что его формулировка окажется логически эквивалентной рекурсивности в смысле Геделя — Черча. Цель формулировки, однако, в том, чтобы предложить систему не только определенной логической силы, но и психологической достоверности. В этом последнем смысле подлежат рассмотрению всё более и более широкие формулировки. С другой стороны, нашей целью будет показать, что все они логически сводимы к формулировке 1. В настоящий момент мы выдвигаем это умозаключение в качестве рабочей гипотезы. … Успех вышеизложенной программы заключался бы для нас в превращении этой гипотезы не столько в определение или аксиому, сколько в закон природы».
Таким образом, гипотеза Поста состоит в том, что любые более широкие формулировки в смысле алфавита символов ленты, набора инструкций, представления и интерпретации конкретных проблем сводимы к формулировке 1.
Следовательно, если гипотеза верна, то любые другие формальные определения, задающие некоторый класс алгоритмов, эквивалентны классу алгоритмов, заданных формулировкой 1 Эмиля Поста.
Обоснование этой гипотезы происходит сегодня не путем строго математического доказательства, а на пути эксперимента – действительно, всякий раз, когда нам указывают алгоритм, его можно перевести в форму программы машины Поста, приводящей к тому же результату.
В дальнейшем работа машины Поста была уточнена следующим образом.
Машина Поста не есть реально существующее, сделанное кем-то устройство. Она представляет собой мысленную конструкцию, существующую лишь в нашем воображении.
Машина Поста состоит из ленты и каретки (называемой также считывающей и записывающей головкой). Лента бесконечна и разделена на секции одинакового размера; для наглядности ленту считают расположенной горизонтально:
Лента бесконечна лишь для простоты изложения. Можно предположить, что лента не бесконечная, а лишь неограниченно растущая в обе стороны: например, можно считать, что лента наращивается на одну секцию, как только каретка доходит до конца ленты и должна двигаться дальше, или что за каждую единицу времени слева и справа нарастает по одной секции. Удобнее, однако, считать, что все секции слева и справа уже наросли, и тем самым, хотя и в ущерб реальности, полагать ленту бесконечной в обе стороны.
Порядок, в котором расположены секции ленты, подобен порядку, в котором расположены все целые числа. Поэтому естественно ввести на ленте «целочисленную систему координат», занумеровав секции целыми числами …-3, -2, -1, 0, 1, 2, 3, ….
Будем считать, что система координат жестко сопоставима с лентой, и получим таким образом возможность указывать какую-либо секцию ленты, называя ее порядковый номер, или координату.
В каждой секции ленты может быть либо ничего не записано (такая секция называется пустой), либо записана метка V (тогда секция называется отмеченной).
| V | V | V | V |
Информация о том, какие секции пусты, а какие отмечены, образует состояние ленты. Иными словами, состояние ленты – это функция, которая каждому числу (номеру секции) ставит в соответствие либо метку, либо пустой символ. Состояние ленты меняется в процессе работы.
Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит ровно против одной секции ленты. Говорят, что каретка обозревает эту секцию, или держит ее в поле зрения.
Информация о том, какие секции пусты, а какие отмечены и где стоит каретка, образует состояние машины Поста. Таким образом, состояние машины слагается из состояния ленты и указания номера той секции, которую обозревает каретка. За единицу времени (которую называют шагом) каретка может сдвинуться на одну секцию влево или вправо. Кроме того, каретка может поставить (напечатать) или уничтожить (стереть) метку в той секции, против которой она стоит, а также распознать, стоит или нет метка в обозреваемой ею секции.
Работа машины Поста состоит в том, что каретка передвигается вдоль ленты и печатает или стирает метки. Эта работа происходит по инструкции определенного вида, называемой программой.
Каждая программа машины Поста состоит из команд. Командой машины Поста будем называть выражение, имеющее один из следующих шести видов (
):
| № п/п | Название | Обозначение | Действие |
| 1 | Команды движения вправо | 
| каретка сдвигается на одну секцию вправо |
| 2 | Команды движения влево | 
| каретка сдвигается на одну секцию влево |
| 3 | Команды печатания метк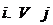и |  ; или 
| каретка печатает метку на обозреваемой секции (выполнение этой команды возможно лишь в том случае, если обозреваемая перед началом выполнения команды секция пуста, в противном случае команда считается невыполнимой) |
| 4 | Команды стирания метки |  или 
| каретка стирает метку в обозреваемой секции (выполнение этой команды возможно лишь в том случае, если обозреваемая секция отмечена, в противном случае команда считается невыполнимой) |
| 5 | Команды передачи управления | i.? j1, j2 | если секция, обозреваемая перед началом выполнения команды, была пуста, то следующей должна выполняться команда с номером j1, если же эта секция была отмечена, следующей должна выполняться команда с номером j2; состояние ленты при этом не изменяется |
| 6 | Команды остановки | i. стоп | машина останавливается |
Например, 
является командой движения вправо, 
– командой передачи управления.
Число i, стоящее в начале команды, называется номером команды. Число j, стоящее в конце команды (а у команд передачи управления – каждое из чисел j1 и j2), будем называть отсылкой (при этом в команде передачи управления j1 – верхней, а j2 – нижней отсылкой).
Программой машины Поста будем называть конечный непустой (т.е. содержащий хотя бы одну команду) список команд машины Поста, обладающий следующими двумя свойствами:
1) На первом месте в этом списке стоит команда с номером 1, на втором месте (если оно есть) – команда с номером 2 и т.д.; вообще на k -м месте стоит команда с номером k.
2) Отсылка любой из команд списка совпадает с номером некоторой (другой или той же самой) команды списка (более точно: для каждой отсылки каждой команды списка найдется в списке такая команда, номер которой равен рассматриваемой отсылке).
Например, следующий список будет программой машины Поста:
1. стоп
2.? 4, 1
3. С 3
4. стоп
А эти два списка не будут программами машины Поста, хотя и составлены из команд машины Поста:
2.? 4, 1 1. стоп
1. стоп 2.? 4, 5
3. С 3 3. С 3
4. стоп 4. стоп
(не выполнено первое условие); (не выполнено второе условие).
Как правило, программы машины Поста записывают в столбик. Число команд программы называется длиной программы.
Чтобы машина Поста начала работать, надо задать, во-первых, некоторую программу, а во-вторых, некоторое ее (машины) состояние, т.е. как-то расставить метки по секциям ленты (в частности, можно все секции оставить пустыми) и поставить каретку против одной из секций. Если секции пронумерованы, то предполагается, что в начальном состоянии (т.е. задаваемом вначале) машины каретка ставится всегда против секции с номером (координатой) нуль. При таком соглашении начальное состояние машины полностью определено состоянием ленты.
Программа является той инструкцией, на основании которой работает машина. Работа машины на основании заданной программы (и при заданном начальном состоянии) происходит следующим образом. Машина приводится в начальное состояние и приступает к выполнению первой команды программы. Эта команда выполняется за один шаг, после чего машина приступает к выполнению той команды (назовем его a), номер которой равен отсылке (одной из отсылок, если их две) первой команды. Эта команда также выполняется за один шаг, после чего начинается выполнение команды, номер которой равен отсылке команды с номером a. Вообще каждая команда выполняется за один шаг, а переход от выполнения одной команды к выполнению другой происходит по следующему правилу: пусть на k -м шаге выполнялась команда с номером i, тогда, если эта команда имеет единственную отсылку j, то на k+1 -м шаге выполняется команда с номером j. Если эта команда имеет две отсылки j1 и j2, то на k+1 -м шаге выполняется одна из двух команд – с номером j1 или с номером j2 в соответствии с состоянием обозреваемой ячейки. Если, наконец, выполняющаяся на k -м шаге команда вовсе не имеет отсылки, то на k+1 -м шаге и на всех последующих шагах не выполняется никакая команда: машина останавливается.
Если теперь, задавшись программой и каким-либо начальным состоянием, пустить машину в ход, то осуществится один из следующих вариантов:
1) В ходе выполнения программы машина дойдет до выполнения невыполнимой команды (печатания метки в непустой секции или стирания метки в пустой секции); выполнение программы тогда прекращается, машина останавливается; происходит так называемая безрезультатная остановка.
2) В ходе выполнения программы машина дойдет до выполнения команды остановки; программа в этом случае считается выполненной, машина останавливается; происходит так называемая результативная остановка.
3) В ходе выполнения программы машина не дойдет до выполнения ни одной из команд, указанных в первых двух вариантах; выполнение программы при этом никогда не прекращается, машина никогда не останавливается; процесс работы машины происходит бесконечно.
Примеры выполнения программ.
Пример 1. Пусть имеется следующая программа машины Поста:
1. V 4
2. С 3
3. 
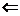2
4. 
5
5.? 4, 3
Применим эту программу к следующему начальному состоянию (закрашенная клетка будет означать обозреваемую в данный момент ячейку):
| V |
– начальное состояние
На первом шаге будет выполняться команда № 1. После первого шага состояние машины станет таким:
| V | V |
Следующей будет выполняться команда, на которую отсылает команда № 1, т.е. команда № 4:
| V | V |
Теперь надо выполнить команду под номером 5 (т.к.отсылка команды № 4 равна 5):
| V | V |
Состояние ленты при этом не изменится. Поскольку обозреваемая секция при этом пуста, то следующей должна выполняться команда, номер которой равен верхней (первой) отсылке, т.е. № 4:
| V | V |
Теперь снова выполняем команду под номером 5:
| V | V |
На этот раз обозреваемая секция отмечена, поэтому следующей будет выполняться команда с номером, равным нижней (второй) отсылке, т.е. команда с номером 3:
| V | V |
Команда № 3 делает отсылку на команду № 2, которая предписывает стереть метку в обозреваемой секции. Но машина сделать этого не может, т.к. обозреваемая в данный момент секция пуста. Следовательно, происходит безрезультатная остановка.
Пример 2. Пусть дано начальное состояние машины Поста:
| V |
Применим к этому начальному состоянию программу:
1. 2
2. 3
3. V 1.
Машина сделает два шага, а на третьем произойдет безрезультатная остановка:
| V |
1 шаг:
| V |
2 шаг:
3 шаг: машина должна напечатать метку в обозреваемой ячейке, но она там уже есть.
Безрезультатная остановка.
Применим к этому же начальному состоянию следующую программу:
1. 2
2. 3
3. стоп.
Машина сделает два шага, а затем на третьем произойдет результативная остановка.
Применим к этому же начальному состоянию программу:
1. 1.
Машина будет работать бесконечно.
Точно так же различные варианты может давать одна и та же программа, примененная к различным начальным состояниям.
Пример 3. Рассмотрим программу:
1.? 4, 1
2. С 3
3. 3. стоп
4. 2.
Применим ее последовательно к начальным состояниям:
| V |
А)
| V |
Б)
| V |
В)
Для начального состояния А получим результативную остановку на четвертом шаге, для Б – бесконечную работу машины, для В – безрезультатную остановку на третьем шаге.
Вопросы для контроля
1. Что изучает теория алгоритмов?
2. Приведите примеры описаний понятия алгоритм
3. Перечислите свойства алгоритмов
4. Приведите примеры алгоритмов, решающих какие-либо житейские задачи.
5. Для чего нужно вводить строгое математическое определение алгоритма?
6. Опишите формализацию понятия алгоритма с помощью машины с неограниченными регистрами (МНР).
7. Дайте определение МНР-вычислимой функции. Приведите примеры МНР-вычислимых функций.
8. Сформулируйте тезис Черча.
9. Опишите формализацию понятия алгоритма с помощью машины Поста.
10. В чем сущность гипотезы Поста?
