Введем теперь следующее определение.

ОСНОВНЫЕ ПОНЯТИЯ

Оглавление.

1. Основные формулы комбинаторики.

2. Случайные события. Частота. Вероятность.

3. Аксиомы вероятностей.

4. Классическое определение вероятности.

5. Условная вероятность. Теорема умножения вероятностей.

6. Формула полной вероятности.

7. Формула Бейеса.

1. Основные формулы комбинаторики.

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Ниже приведены самые распространенные из них:

Перестановками называют комбинации, состоящие из одних и тех же различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок:

, .

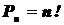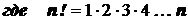По определению, .

Размещениями называют комбинации, составленные из различных элементов по элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

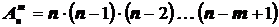Либо .

Сочетаниями называют комбинации, составленные из различных элементов по элементов, которые отличаются хотя бы одним элементом. Число сочетаний

Числа размещений, перестановок и сочетаний связаны равенством

Замечание: выше предполагалось, что все элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Например, если среди элементов есть элементов одного вида, элементов другого вида и т. д., то число перестановок с повторениями:

, где .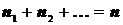

При решении задач комбинаторики используют следующие правила:

Правило суммы: если некоторый объект может быть выбран из совокупности объектов способами, а другой объект может быть выбран способами, то выбрать либо , либо можно способами.

Правило произведения: если объект можно выбрать из совокупности объектов способами и после каждого такого выбора объект можно выбрать способами, то пара объектов в указанном порядке может быть выбрана 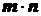способами.

2. Случайные события. Частота. Вероятность.

Теория вероятностей — математическая наука, изучающая закономерности массовых, случайных явлений (событий).

Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).

Если, например, испытание состоит в бросании монеты, то выпадение герба является событием. Если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие. Если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от до 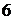, тo выпадение пятерки — событие.

При подбрасывании монеты вероятность выиграть составляет 1/2, а при бросании игральной кости выигрышем считается выпадение цифры шесть (вероятность выигрыша 1/6). Чему равна вероятность проигрыша в каждом случае? Значит ли это, что играть в кости менее выгодно?

Обсуждение

В каждом из двух случаев вероятность выиграть и проиграть должны составить в сумме 100% или единицу, поскольку ничейный вариант в этих ситуациях невозможен. Это означает, что при бросании монеты вероятность проиграть равна 1/2, а при бросании игральной кости - 5/6. А вот вопрос о "выгодах" предложения поиграть в кости по сравнению с предложением бросить монету не так прост, как это кажется. Оставив на минуту в стороне азартные игры, обсудим одну важную для бизнеса проблему. Решение о "выгодности" любого предпринимаемого нами действия, очевидно, зависит не только от нашей оценки риска данного предприятия, но и от величины предполагаемого выигрыша по сравнению с нашими ставками. Чем меньше шансов получить выигрыш, тем больше должна быть величина этого выигрыша по сравнению со ставкой, чтобы сделать игру привлекательной для потенциальных игроков. Забота о привлекательности условий игры, конечно, распространяется только на те случаи, когда игроки принимают решение об участии в процессе добровольно и осмысленно. Так, чем рискованнее финансовые вложения, тем большую прибыль мы ожидаем получить в результате. Когда соотношение "риск - прибыльность" кажется нам неподходящим, мы ищем возможности покинуть "игру". Поэтому при любой оценке бизнес-проекта оценка рисков не менее важна, чем оценка прибыльности, по сути, это - неотъемлемая часть финансово-экономического анализа. Возвращаясь к нашему заданию, пришло время обсудить финансовые условия игры. Какой именно выигрыш покажется нам справедливым и почему? Если при бросании монеты участвуют два игрока, сделавшие одинаковые ставки, причем выигравший забирает все, то возможный выигрыш в такой игре должен вдвое превышать исходную ставку. Менее очевидный случай - бросание кости. Должен ли выигрыш в шесть раз превышать ставку игрока, и откуда возьмется эта сумма, если игроков по-прежнему только двое? Вот если бы игроков было шестеро, и каждый поставил бы на разную цифру, то при одинаковых исходных ставках получилась бы вполне справедливая игра. Выигравший забрал бы в шесть раз больше, чем поставил, но шансы каждого игрока выиграть были бы одинаковыми. Если же играют двое, причем один выигрывает, только при выпадении цифры "шесть", значит второй выигрывает при любой другой ситуации, и его шансы на выигрыш в пять раз выше. Само по себе это не означает, что игра "нечестная", просто справедливые правила должны потребовать от второго игрока сделать исходную ставку, которая будет в пять раз выше, чем ставка первого игрока.

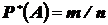События будем обозначать заглавными буквами латинского алфавита: . Пусть при испытаниях событие появилось раз. Отношение называется частотой (относительной частотой) события и обозначается . Опыт показывает, что при многократном повторении испытаний частота случайного события обладает устойчивостью.

Устойчивость относительных частот появления в различных сериях достаточно большого числа испытаний можно проиллюстрировать на таком примере.

Опыт	Число опытов,	Появление герба,
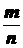
Опыт Керриха	10 000	5 087	0,5087
Опыт Бюффона	4 040	2 048	0,5069
1 Опыт Пирсона	12 000	6 019	0,5016
2 Опыт Пирсона	24 000	12 012	0,5005

Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события будем обозначать через . В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.

Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.

Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.

Если событие достоверно, то оно произойдет при каждом испытании . Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится . Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.

Если событие не является ни достоверным, ни невозможным, то его частота при большом числе испытаний будет мало отличаться от некоторого числа — вероятности события .

- вероятность события , - численное значение этой вероятности. Если , то 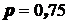. Пишут , но не пишут .

На практике очень часто имеют дело с несколькими событиями, которые находятся между собой в некоторых отношениях. Поэтому рассмотрим эти различные отношения между событиями.

Совмещением (или произведением) двух событий и называется событие, состоящее в совместном наступлении как события , так и события . Это событие будем обозначать или .

Аналогично, совмещением нескольких событий, например , и , называется событие , состоящее в совместном наступлении событий , и .

Объединением (или суммой) двух событий и называется событие , заключающееся в том, что произойдет по крайней мере одно из событий или . Это событие обозначается так: .

Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.

Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.

Рассмотрим следующий пример. Будем следить за движением какой-нибудь определенной молекулы газа, заключенного в некоторый объем. Внутри этого объема выделим объемы и, частично перекрывающие друг друга (рис. 1). Пусть событие A — попадание молекулы в объем , событие В — попадание молекулы в объем . Совмещением событий A и В является попадание молекулы в общую часть объемов и . Если объемы и не имеют общих точек, то ясно, что события A и В несовместны. Объединением событий A и В является попадание молекулы или только в объем или только в объем , или же в их общую часть.

3. Аксиомы вероятностей.

Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло раз, а событие В произошло раз. Тогда частоты событий A и В соответственно равны , . Так как события A и В несовместны, то событие A+B в данной серии опытов произошло раз. Следовательно,

Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то

P(A+B)=P(A)+P(B).

Изложенное позволяет высказать следующие свойства вероятностей, которые можно принять в качестве аксиом.

Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию .

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:

(1.1)

Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события , попарно несовместны, то

(1.2)

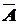Событием, противоположным событию , называется событие , состоящее в ненаступлении события . Очевидно, события и 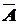несовместны.

Пусть, например, событие состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие 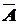заключается в том, что изделие стандарту не удовлетворяет. Пусть событие - выпадение четного числа очков при однократном бросании игральной кости; тогда 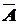— выпадение нечетного числа очков.

Теорема 1. Для любого события вероятность противоположного события 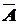выражается равенством

(1.3)

Доказательство. Событие , состоящее в наступлении или события , или события 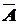, очевидно, является достоверным. Поэтому на основании аксиомы 2 имеем . Так как события и 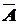несовместны, то используя аксиому 3, получим . Следовательно, , откуда .

Теорема 2. Вероятность невозможного события равна нулю.

Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.

4. Классическое определение вероятности.

Как было сказано выше, при большом числе n испытаний частота P*(A)=m/ n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е. .

Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. Ведь нам нужно заранее знать вероятность некоторого события, еще до опыта. В этом и состоит эвристическая, предсказательная роль науки. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).

Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.

Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.

Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).

События 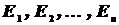в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.

Очевидно, любое событие A и противоположное ему событие 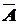образуют полную группу.

Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A. Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A.

Пусть события 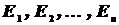в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют исходов испытания. Тогда вероятностью события A в данном опыте называют отношение . Итак, мы приходим к следующему определению.

Вероятностью P(A) события в данном опыте называется отношение числа исходов опыта, благоприятствующих событию A, к общему числу возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий: .

Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.

Пример 1.1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.

Решение: Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из равновероятных исходов, из которых событию A благоприятствуют исходов. Поэтому .

Пример 1.2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми?

Решение: Число всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2 (полная группа событий):

Число благоприятствующих исходов (сколькими способами можно из 3 шаров выбрать 2): . Следовательно, искомая вероятность .

Забегая вперед, эту задачу можно решить и другим способом.

Решение: Вероятность того, что при первом испытании (вытаскивании шара) будет вынут белый шар, равна (всего шаров 10, из них 3 белых). Вероятность того, что при втором испытании будет вынут снова белый шар равна (всего шаров стало 9, т.к. один вынули, белых стало 2, т.к. вынули именно белый). Следовательно, вероятность совмещения событий равна произведению их вероятностей, т.е. .

Пример 1.3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара?

Решение: Находим соответственно вероятности появления зеленого, красного и коричневого шаров: ; ; . Так как рассматриваемые события, очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность появления цветного шара:

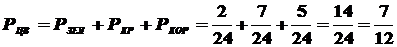Либо, другим способом. Вероятность появления белого шара равна . Тогда вероятность появления небелого шара (т.е. цветного), т.е. вероятность противоположного события, равна .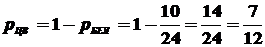

Геометрическое определение вероятности. Чтобы преодолеть недостаток классического определения вероятности (оно неприменимо к испытаниям с бесконечным числом исходов), вводят геометрические определение вероятности - вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок составляет часть отрезка . На отрезке наудачу поставлена точка, что означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка , вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка . В этих предположениях вероятность попадания точки на отрезок определяется равенством

. (1.4)

Далее, пусть плоская фигура составляет часть плоской фигуры . На фигуру наудачу брошена точка, что означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры , вероятность попадания брошенной точки на фигуру пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно , ни от формы . В этих предположениях вероятность попадания точки в фигуру определяется равенством

. (1.4a)

Замечание: в случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае же геометрического определения вероятности обратные утверждения не имеют места.

5. Условная вероятность. Теорема умножения вероятностей.

Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В.

Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:

	1-я монета	2-я монета
1-й исход	герб	герб
2-й исход	герб	надпись
3-й исход	надпись	герб
4-й исход	надпись	надпись

Таким образом, .

Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:

	1-я монета	2-я монета
1-й исход	герб	герб
2-й исход	герб	надпись

При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях . Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.

Новую вероятность события А, в предположении, что произошло событие B, будем обозначать . Таким образом, ; .

Теорема 3 (теорема умножения). Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.

(1.5)

Доказательство. Докажем справедливость соотношения (5), опираясь на классическое определение вероятности. Пусть возможные исходы 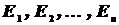данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют исходов, и пусть из этих исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из возможных результатов испытания. Это дает , , .

Таким образом, . Поменяв местами A и B, аналогично получим:

(1.6)

Из формул (5) и (6) имеем

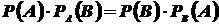(1.7)

Теорема умножения легко обобщается на любое, конечное число событий. Так, например, в случае трех событий имеем (Событие можно представить как совмещение двух событий: события 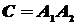и события )

В общем случае

(1.8)

Введем теперь следующее определение.

Два события A и B называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т. е. если

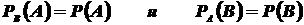(1.9)

Если я несколько раз кидаю игральную кость, и хочу, чтобы выпала "шестерка", а мне все время не везет, значит ли это, что надо увеличивать ставку, потому что, согласно теории вероятностей, мне вот-вот должно повезти? Увы, теория вероятности не утверждает ничего подобного. Ни кости, ни карты, ни монетки не умеют запоминать, что они продемонстрировали нам в прошлый раз. Им совершенно не важно, в первый раз или в десятый раз сегодня я испытываю свою судьбу. Каждый раз, когда я повторяю бросок, я знаю только одно: и на этот раз вероятность выпадения "шестерки" снова равна одной шестой. Конечно, это не значит, что нужная мне цифра не выпадет никогда. Это означает лишь то, что мой проигрыш после первого броска и после любого другого броска - независимые события.

Из соотношения (7) вытекает, что из двух равенств (8) одно является следствием другого.

Пусть, например, событие A — появление герба при однократном бросании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы.

В случае независимости событий A к B формула (5) примет более простой вид:

(1.10)

т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.

События 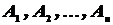называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.

Исходя из этого определения, в случае независимости событий 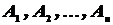между собой в совокупности на основании формулы (8) имеем

(1.11)

Пример 1.4. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз?

Решение: Пусть событие — появление герба при 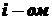бросании. Искомая вероятность есть вероятность совмещения всех событий , а так как они, очевидно, независимы в совокупности, то, применяя формулу (11), имеем

Но для любого i; поэтому

Пример 1.5. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего.
Решение:
1) Искомую вероятность р находим по формуле (11):

2) Вероятность того, что в течение часа станок потребует внимания рабочего для первого станка равна 1—0,9=0,1, для второго и для третьего станков она соответственно равна 1—0,8=0, 2 и 1—0,7=0,3. Тогда вероятность того, что в течение часа все три станка потребуют внимания рабочего, на основании формулы (10) составляет

Событие A, заключающееся в том, что в течение часа все три станка потребуют внимания рабочего, противоположно событию 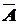, состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем

Пример 1.6. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?

Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (6). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем

Но ; , поскольку после того, как был вынут первый белый шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,

Пример 1.7. В урне имеется красных, синих и белых шара. Каждое испытание состоит в том, что из урны берут на удачу один шар и не возвращают обратно. Какова вероятность того, что при первом испытании будет вынут красный шар (событие ), при втором – синий (событие ), при третьем – белый (событие ).

Решение. Поскольку , , , то согласно формуле

получим:

Пример 1.8. В каждом из трех ящиков имеется по детали; при этом в первом ящике , во втором , в третьем стандартные детали. Из каждого ящика берут по одной детали. Найти вероятность того, что все три извлеченные детали окажутся стандартными.

Решение. Пусть извлечение стандартной детали из первого ящика - событие , из второго - событие , из третьего - событие . Тогда , , .

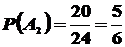Согласно формуле получим .

Пример 1.9. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна , вторым - , третьим - . Найти вероятность того, что: а) только один из стрелков попадет в цель; б) только два стрелка опадут цель; в) все три стрелка попадут в цель.

Решение. а). Введем обозначения: поражение цели первым стрелком - событие , вторым - , третьим - . Попадание в цель только первым стрелком - событие , только вторым стрелком - , только третьим - . Пусть , , , тогда , , 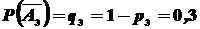. Поскольку 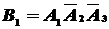, , 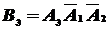и события , , несовместны, то вероятность того, что только один стрелок попадет в цель будет выражаться формулой . Так как , , , то

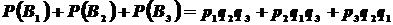
Подставляя данные, получим: вероятность попадания в цель только одного (не важно какого) стрелка равна

б). Пусть событие - попадание в цель только вторым и третьим стрелками, - только первым и третьим стрелками, - только первым и вторым стрелками. То есть , , 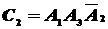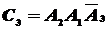. Тогда вероятность того, что только два (неважно какие) стрелка попадут в цель выразится формулой:

Подставляя данные, получим: вероятность попадания в цель только двух (не важно каких) стрелков равна

б). Вероятность того, что все три стрелка попадут в цель, будет равна

6. Формула полной вероятности.

Пусть событие A может произойти только вместе с одним из попарно несовместных событий , образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий : либо , либо , либо и т.д. Следовательно,

Применяя аксиому сложения вероятностей, имеем

Но ,

поэтому

(1.12)

Эта формула называется формулой полной вероятности. События часто называют «гипотезами».

Пример 1.10. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах. C 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?

Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны:

Далее, из условия задачи следует, что

Используя формулу полной вероятности (11), имеем

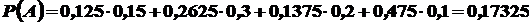
7. Формула Бейеса.

Предположим, что будет производится некоторый опыт, причем об условиях его проведения можно высказать n (единственно) возможных и несовместных гипотез , имеющих вероятности . Пусть в результате проведения этого опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы , то .

Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей .

На основании соотношений (5) и (6) имеем

Откуда .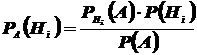

Но по формуле полной вероятности

Поэтому

(1.13)

Формула (13) называется формулой Бейеса (Т. Бейес (ум. 1763) - английский математик.).

Пример 1.11. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460 —на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом?

Решение: Пусть A — событие, состоящее в том, что взятый подшипник нестандартный, а 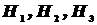- гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют

Из условия задачи следует, что

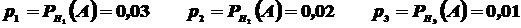
Найдем , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем

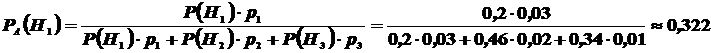
Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.

Пример 1.12. Команда стрелков состоит из человек. из ни попадают в цель с вероятностью , а двое - с вероятностью . Наудачу из команды берется стрелок и производит выстрел.

а). Какова вероятность того, что стрелок попадет.

б). Если стрелок попал в цель, то какова вероятность, что это один из трех (один из двух).

Решение.

а). Событие (попадание стрелком в цель) может произойти, если произойдет одно из несовместных событий: - наудачу взятый стрелок один из трех, - наудачу взятый стрелок один из двух. Для определения вероятности события воспользуемся формулой (17):

б). По формуле (18):

Или .