Лекция 15. Нагрев основного металла при сварке.  

План лекции.. Классификация источников тепла. Модели тепловых полей при действии мнгновенных, непрерывнодействующих, неподвижных, подвижных, быстродвижущихся источников. Нагрев тел вращения, движение источника вблизи края тела, нагрев двух узких пластин. Определение размеров зон нагрева. Распределённые источники теплоты.

Классификация источников тепла. Нагрев тел может осуществляться разнообразными источни­ками теплоты, различающимися между собой по распределенно­сти, времени действия и движению их относительно тела. При определенных условиях все многообразие источников теплоты можно получить, пользуясь мгновенным точечным источником теплоты.

   Мгновенный точечный источник теплоты — понятие абстракт­ное. Физической схемой, примерно соответствующей мгновенному точечному источнику, можно считать такую, при которой в очень малый объем за весьма малый промежуток времени вводится некоторое количество теплоты Q. Формально такое введение теплоты можно рассматривать как граничное условие при t = 0, когда вместо распределения температур задается распределение теплоты в теле. Действительно, если принять, что во всех точках тела, кроме одной, теплосодержание равно нулю, а в точке с координатами X_{0 j}, Y₀, Z₀ при t = 0 содержится количество теп­лоты Q, то будем иметь случай мгновенного точечного источ­ника.

   В последующие моменты времени теплота будет распростра­няться по телу, подчиняясь уравнению теплопроводности.

    Если воспользоваться принципом наложения, то, комбини­руя мгновенные точечные источники, можно получить множество иных источников теплоты. Принципом наложения можно поль­зоваться при условии, что теплофизические коэффициенты счи­тают независящими от температуры, а выделением и поглоще­нием теплоты в процессе фазовых превращений пренебрегают. Принцип наложения заключается в сложении температур от дей­ствия отдельных источников, которые находятся в разных точках тела, или выделяют теплоту в разные моменты вре­мени, либо и находятся в разных точках тела, и выделяют теп­лоту неодновременно.

  Модели тепловых полей при действии мнгновенных, непрерывнодействующих, неподвижных, подвижных, быстродвижущихся источников.

   Мгновенный линейный источник теплоты представляет собой комбинацию мгновенных точечных источников, действующих одновременно и расположенных по линии. Распределение Q по линии действия ряда мгновенных точечных источников может выражаться различными функциями. Равномерное распределе­ние Q по линии (рис. 15.1, а) означает действие мгновенного линейного источника. В случае распределения Q по нормальному закону (рис. 15.1,6) имеем нормально линейный мгновенный источник.

Мгновенный плоский источник теплоты представляет собой совокупность мгновенных точечных источников теплоты, дейст­вующих одновременно и расположенных в одной плоскости. Рас­пределение теплоты Q при /=0 может иметь разнообразный характер. Под мгновенным плоским источником обычно пони­мают равномерное распределение Q по сечению (рис. 15.1, в). В случае нормального распределения Q по кругу имеем мгновен­ный нормально круговой плоский источник (рнс. 1 5.1,г).

Мгновенный объемный источник теплоты представляет собой совокупность мгновенных точечных источников, распределенных по какому-либо закону в теле.

Используя принцип наложения, удается получить различные мгновенные источники, отличающиеся по распределенности. По существу только точечный источник сосредоточен по отношению ко всем координатным осям, линейный источник сосредоточен по отношению к двум координатным осям и распределен в третьем направлении, а плоский — сосредоточен лишь в одном направ­лении.

Объемный источник может служить примером распределен­ного источника по всем направлениям.

       Рисунок 15.1 Расчётные схемы мнгновенных источников теплоты.

        а) – линейный источник в пластине; б) – нормально линейный источник;

        в) – плоский источник в стержне; г) – нормально круговой источник на поверхности 

               полубесконечного тела.

Рисунок 15.2  Движущийся   точечный источник на поверхности полубесконечного тела.

Непрерывно действующие и движущиеся источники теплоты представляют собой совокупность мгновенных источников, рас­пределенных по промежутку времени действия источника. На­пример, точечный источник может действовать непрерывно в течение определён-ного отрезка времени t. В этом случае он уже не будет мгно­венным, так как теплота выделяется в точке постепенно.

Источники теплоты могут быть не­подвижные, движущиеся и быстродвижущиеся. Очевидно, что движущийся источник не может быть мгновенным, так как предполагается, что его движе­ние протекает в течение некоторого отрезка времени, когда выделяется теплота. Точечный непрерыв­но действующий источник, продвигающийся из точки О в направ­лении х (рис. 15. 2), представляет собой движущийся источник

 

 

                             Начнем с рассмотрения распространения тепла мгновенных источников, сосредоточенных

в точке, линии или плоскости в телах различных принятых схем.

   =  Предположим, что в некоторой точке О бесконечного тела в течение короткого времени

внесено тепло Q (кал или Дж). Если считать, что границы тела не искажают теплового потока (они удалены в бесконечность) и в начальный момент температура тела Т₀ постоянна по всему объему и равна нулю, то уравнение теплопроводности примет вид:

 

где T(R,t) – температура в ⁰С рассматриваемой точки, находящейся на расстоянии R, см

от точки О через t сек от момента внесения тепла, R = √(x2 + y2 + z2), где x, y, z – расстояния в см по координатным осям от рассматриваемой точки до точки О, являющейся началом координат);

   с – удельная теплоемкость тела, кал/(г×⁰С);

  r – плотность тела, г/см ³;

   а – коэффициент температуропроводности, см²/с.

= Если тело полубесконечное с расположением точки О на его поверхности (z = 0) и эту

п оверхность считать не отдающей тепла в окружающую среду, то все тепло будет

распространяться не по всем направлениям, а только в одну половину бесконечного тела.

Каждая точка получит тепла вдвое больше, чем бесконечного:

                                                 

    =  Для линейного источника, вводящего тепло в пластину толщиной см, при принятых

условиях (граничные поверхности z = 0 и z = δ не пропускают тепло) решение дифферен-

циального уравнения теплопроводности примет вид:

где r – расстояние рассматриваемой точки от источника тепла;

в данном случае r = √(x2 + y2), так как тепловой поток плоский и от z не зависит.

Изотермы представляют собой цилиндры с общей осью z, проходящей перпендикулярно

к поверхности пластины через точку О.

   = Если в бесконечный стержень по одному из его сечений F плоским источником

мгновенно введено тепло Q, то оно (при отсутствии отвода тепла через боковые поверхности

в окружающую среду) распределится только по оси х­x.:

где х – координата рассматриваемого сечения от сечения, в которое вводилось тепло.

Изотермы в этом случае представляют собой плоскости, параллельные плоскости

ввода тепла.

Упрощенно в рассмотренных схемах можно учесть и поверхностную теплоотдачу

в окружающую среду введением в правую часть дополнительного сомножителя e^­bt,

где b – коэффициент температуроотдачи, зависящий от α – коэффициента теплоотдачи,

объемной теплоемкости и формы тела.

Для реальных случаев распространения тепла при сварке в полубесконечных телах

поверхностная теплоотдача играет небольшую роль и ею можно пренебречь.

Для пластин, особенно тонких, эти потери могут играть существенную роль.

В этом случае b = 2α/(cρδ). Коэффициент 2 указывает на отдачу тепла в среду по двум

поверхностям z = 0, z = δ.

Для стержней b = p α /(c F ρ), где p – периметр стержня, см; F – его поперечное

сечение, см2. Тогда для пластины

для стержня

   = Для условий сварки, особенно плавлением, основное значение имеют не мгновенные,

а непрерывно действующие подвижные источники постоянной мощности. В этих условиях для получения уравнений процесса распространения тепла используют принцип наложения,

позволяющий рассматривать температуру в любой точке как результат суммирования

действия тепловых потоков мгновенных источников, произвольно расположенных в объеме

тела. Для этого весь период действия непрерывно действующего источника разбивают

на бесконечно малые элементы и рассматривают отдельные элементарные воздействия.

В случае подвижного источника учитывают и изменение расстояния от каждого мгновенного

источника до рассматриваемого объема (точки). В подвижной системе координат

(не связанной с телом, а перемещающейся вместе с источником) это решение даст

следующие зависимости. Для полубесконечного тела:

 

             

 

 

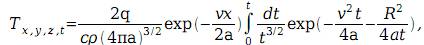
где R² = x² + y² +z² – квадрат пространственного радиуса­вектора точки температурного

поля.

Для линейного источника в пластине

где r ² = x² + y².

Для плоского источника в стержне

Эти уравнения являются основой для ряда решений применительно к условиям сварки.

Рассмотрим предельное или установившееся состояние применительно к сварке массивного тела точечным источником тепла. Полагая в предыдущей формуле t → ∞, получим предельное

состояние в виде уравнения в подвижной системе координат:

При неподвижном источнике v = 0

Единичная дельта - функция (функция Дирака). Производная от функции Хевисайда δ₁(x), сама единичная дельта-функция выглядит так:

Рисунок 15.3. Функция Дирака (δ-функция).

Формула для неё:

               0 при x < 0

δ(x) =                  ∞ при x = 0

               0 при x > 0

То, что дельта-функция в нуле равна бесконечности - это условность, которая нужна главным образом для физической интерпретации.

Таким образом вводится единичная дельта-функция. Если взять от неё неопределённый интеграл, то должна получиться функция δ₁(x) + С, где C - константа, δ₁(x) - функция Дирака ("единичная ступенька"), о которой говорилось выше - первообразная дельта-функции.