Если известна фундаментальная система решений у 1, у 2,..., у n однородного уравнения (8), то общее решение соответствующего неоднородного уравнения (7) можно найти методом вариации произвольных постоянных (методом Лагранжа). Этот метод можно применять при решении линейного неоднородного уравнения (7) как с переменными, так и с постоянными коэффициентами. При этом, если правая часть неоднородного уравнения с постоянными коэффициентами (14) не является частным случаем формулы (15), то этот метод позволяет найти решение. Суть метода заключается в следующем.
Общее решение уравнения (7) записывают в виде
у = С1(х) у 1 + С2(х) у 2 +... +С n (х) у n,
где у 1, у 2,..., у n — линейно независимые частные решения уравнения (8), а функции С1(х), С2(х),..., С n (х) находят из системы уравнений:
|
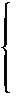
Система (17) всегда имеет решения, т.к. её определитель является определителем Вронского, а W (x) ¹ 0 (п. 2.2).
Пример 1. Найти общее решение уравнения
y ' + x ∙ y ''= x 2. (18)
Решение. Данное уравнение является линейным неоднородным уравнением второго порядка. Решим его методом вариации произвольных постоянных.
1. Найдём общее решение соответствующего линейного однородного уравнения
x ∙ y '' + y ' = 0. (19)
Данное уравнение является дифференциальным уравнением второго порядка, не содержащим искомой функции у. Полагая y ' = z, следовательно, y '' = z, преобразуем уравнение (19) к виду
x ∙ z ' + z = 0.
Таким образом понизили порядок уравнения на единицу и получили уравнение с разделяющимися переменными. Решим его:
Þ 
Þ 
Þ 
.
Возвращаясь к переменной у, опять получим уравнение с разделяющимися переменными: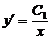 
. Решим его:
Þ 
Þ 
— общее решение линейного однородного уравнения (19). Исходя из вида полученного общего решения, можно допустить, что 
, у 2 = 1 — частные решения уравнения (19).
2. Найдём общее решение данного линейного неоднородного уравнения (18) в виде:
. (20)
Для нахождения функций С 1(х), С 2(х) составим систему уравнений:
(21)
Заметим, что если разделить исходное уравнение (18) на х ¹ 0, получим уравнение
. (22)
Тогда f (x) = х, 
, у 2 = 1 и система (21) примет вид:
Þ 
Последовательно дифференцируя уравнение (20) два раза и учитывая равенства системы, получим:
;
.
Подставив эти выражения вместо y ', y '' в исходное уравнение (22), получим
.
Откуда 
Þ 
Þ 
.
Первое уравнение системы (21) примет вид 
.
Интегрируя его, получим 
.
Таким образом, подставляя найденные значения функций С 1(х) ,С 2(х) в уравнение (20), получим общее решение данного линейного неоднородного уравнения (18):
,
где С 1, С 2 — произвольные постоянные.
Заметим, что при х = 0 исходное уравнение (18) принимает вид y ' = 0. Откуда получим частное решение: у = С.
Пример 2. Найти общее решение уравнения
.
Решение. Данное уравнение является линейным неоднородным уравнением третьего порядка. Решим его методом вариации произвольных постоянных.
1. Найдём общее решение соответствующего линейного однородного уравнения
.
Данное уравнение является линейным однородным уравнением третьего порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение
.
Его корни k 1= 1, k 2= –1, k 3= 2 — простые действительные числа (п. 2.3, случай 1). Следовательно, общее решение однородного уравнения имеет вид
у = С 1 е x + C 2 е -х + C 3 е 2х.
Исходя из вида общего решения, можно допустить, что у 1 = ех, у 2 = е -х, у 3 = е 2х — частные решения однородного уравнения.
2. Найдём общее решение данного линейного неоднородного уравнения в виде
у = С 1(х) е x + C 2(х) е –х + C 3(х) е 2х. (23)
Для нахождения функций С 1(х), С 2(х), С 3(х)составим систему уравнений (17). Она примет вид
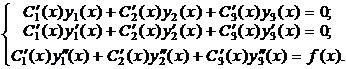Þ
Þ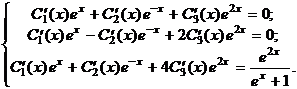 
Решая систему из трёх уравнений с тремя неизвестными, например методом Гаусса, получим:
, 
, 
.
Интегрируя эти выражения, найдём:
;
;
.
Таким образом, подставляя найденные значения функций С 1(х), С 2(х), С 3(х) в уравнение (23), получим общее решение данного линейного неоднородного уравнения:
у = 
е x + 
е -х + 
е 2х =
= С 1 е x + C 2 е -х + C 3 е 2х + 
,
где С 1, С 2, С 3 — произвольные постоянные.
