Определение 15.1. Говорят, что случайная величина Х имеет вероятность или плотность распределения вероятностей, если существует функция p (x) такая, что функция распределения
 =P{ X < x }=
=P{ X < x }=  (1).
(1).
Пример 15.2. Функция распределения случайной величины Х имеет вид 
Найдите плотность распределения.
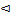 Плотность распределения p (x) и функция распределения
Плотность распределения p (x) и функция распределения  связаны формулой (1), из нее получаем:
связаны формулой (1), из нее получаем:
p (x) =  =
=  =
=  =
=  при
при 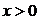 ;
;
p (x) =  =0 при
=0 при 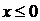 .
.
Таким образом, плотность распределения данной случайной величины определяется следующей функцией
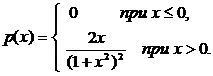
Пример 15.3. Найти функцию распределения  случайной величины Х, плотность вероятности которой определена функцией
случайной величины Х, плотность вероятности которой определена функцией

 Чтобы найти функцию распределения
Чтобы найти функцию распределения  , воспользуемся формулой (1). При
, воспользуемся формулой (1). При  получаем
получаем  =
=  =0.
=0.
При  находим
находим
 =
=  =
=  +
+  =
=  +
+  = 0+
= 0+  =
=  .
.
При  имеем
имеем
 =
=  =
=  +
+ 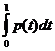 +
+  =
=  +
+  +
+ 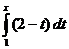 =0+
=0+  + +
+ +  =
=  +(2 x -
+(2 x -  ) – (2 -
) – (2 -  )= -
)= -  + 2 x - 1.
+ 2 x - 1.
При 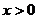 получаем
получаем  =
=  =
=  +
+  =
=  +
+  =1.
=1.
Таким образом, искомая функция распределения имеет вид
Плотность распределения p (x) и функция распределения  связаны формулой (1), из нее получаем:
связаны формулой (1), из нее получаем:
p (x) =  =
=  =
=  =
=  при
при 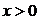 ;
;
p (x) =  =0 при
=0 при 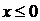 .
.
Таким образом, плотность распределения данной случайной величины определяется следующей функцией

Определение 15.3. Случайная величина называется непрерывной, если она имеет плотность распределения вероятностей.
График функции p (x) (плотности распределения) называется кривой распределения.
Вероятность попадания значений случайной величины X в интервал  равна:
равна:
P{  < X <
< X <  }=
}=  (2).
(2).
Пример 15.4. Плотность распределения случайной величины Х задана функцией

Найти вероятность того, что в результате испытания величина Х примет значение из интервала (1,2).
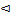 Необходимую вероятность найдем по формуле (2):
Необходимую вероятность найдем по формуле (2):
P{1< X <2 }=  =
= 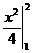 =
=  -
-  = 1-
= 1- 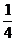 =
=  =0,75.
=0,75. 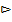
Свойства плотности распределения
Свойство 15.3. F'(x)= p (x).
Свойство 15.4. Плотность распределения – неотрицательная функция p (x) >0.
 Т.к. F(x) - неубывающая функция, то F'(x)
Т.к. F(x) - неубывающая функция, то F'(x)  0, p (x) = F'(x)
0, p (x) = F'(x)  0.
0. 
График плотности распределения называют кривой распределения. Кривая распределения расположена либо над осью O x, либо на оси O х.
Свойство 15.5.  =1.
=1.
 В равенстве (1) вместо x ставим x =+∞, получаем F(+∞)=
В равенстве (1) вместо x ставим x =+∞, получаем F(+∞)=  =1.
=1. 
Свойство 15.6. Вероятность того, что непрерывная случайная величина Х примет значение из множества В равна интегралу по множеству В от плотности распределения:
Р(Х 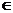 В)=
В)=  .
.
Литература:
1. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман – М.: Высшая школа, 1977 (2004, 2008). – 480 с.
2. Гмурман, В.Е. Руководство к решению задач по ТВ и МС / В.Е. Гмурман – М.: Высшая школа, 1979 (2004, 2008). – 400 с.
3. Мацкевич, И.П. Высшая математика: ТВ и МС / И.П. Мацкевич, Г.П. Свирид – Минск.: Вышэйшая школа, 1993. – 269 с.
4. Еровенко, В.А. Основы высшей математики для филологов: методические замечания и примеры, курс лекций / В.А. Еровенко. – Минск.: БГУ, 2006. – 175 с.
5. Бураковский, В.В. Теория вероятностей и математическая статистика: лабораторный практикум: в 2 ч. Ч. 1 / В.В. Бураковский – Гомель.: ГГУ им. Ф. Скорины, 2002. – 52 с.
6. Свешников, А.А. Сборник задач по теории вероятности, математической статистики и теории случайных функций / А.А. Свешников – М.: Наука, 1965. – 632 с.
7. Кручкович, Г.И. Сборник задач и упражнений по специальным главам высшей математики / Г.И. Кручкович, Г.М. Мордасова, В. А. Подольский, Б. С. Римский-Корсаков, – М.: Высшая школа, 1970. – 512 с.
Учебное издание
БУРАКОВСКИЙ ВЛАДИМИР ВИКТОРОВИЧ
БОРОДИЧ ТИМУР ВИКТОРОВИЧ
Высшая математика
Тексты лекций
Рекомендованы к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины»
Подписано в печать __.__.__. Формат 60x84 1/16. Бумага писчая № 1
Печать офсетная. Гарнитура Таймс. Усл. П. Л. 4,7. Уч.-изд.л. 3,72. Тираж ___ экз.
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
246019, г. Гомель, ул. Советская, 104
Отпечатано на полиграфической технике с оригинала
макета учреждения образования «Гомельский государственный
университет имени Франциска Скорины»
246019, г. Гомель, ул. Советская, 104






