Глава 2. Новые области применения математики в XX веке.

Оглавление

Введение	3
Глава 1. Основные направления развития математики в XX веке	5
1.1. Топология	5
1.2. Риманова геометрия 1.3. Теория вероятности	13 18
Глава 2. Новые области применения математики в XX веке	27
2.1. Математика и развитие компьютерных технологий	27
2.2. Теория вероятности и развитие современных технологий	28
2.3. Использование сведений о современном развитии математики   в начальной школе	34
Заключение	39
Список литературы	41

 

Введение

В отличие от других наук, математика, как представительница чистого разума, развивается поступательно, вне зависимости от увлечений человечества на том или ином историческом промежутке времени, от революций и катаклизмов общества. Иногда математики любят ставить проблемные вопросы, на решение которых уходят столетия. Основой развития математики в XX веке стал сформировавшийся математический язык цифр, символов, операций, геометрических образов, структур, соотношений для формально-логического описания и исследования действительности, развитие информационных технологий. [5]

Актуальность к исследовании темы: «Развитие математики в XX веке» велика, так как на протяжении всего века происходило развитие огромного количества направлений математики. Математика без истории существовать не может, так как на протяжении всех эпох развития она усложнялась, открывались и доказывались новые законы, теоремы, с помощью точных вычислений, доказательств и опытов появились аксиомы, которые точны и не требуют доказательств.

Данную тему я выбрала потому что в XX веке развивалось очень много направлений, которые продолжают развиваться и нести особый интерес к их изучению. Каждое из направлений раскрывает математику с особой стороны, показывает ее уникальность и неповторимость. Именно этим и привлекло меня данное исследование.

Исходя из актуальности рассматриваемой темы, мной выбрана тема исследования: «Основные направления развития математики в XX веке».

Цель:  выделить и раскрыть сущность основных направлений развития математики XX века.

 

Объект исследования: процесс развитияматематика XX века.

Предмет исследования: основные направления развития математики XX века.

Задачи исследования:

1) Рассмотреть основные направления математики XX века;

2) Раскрыть сущность направлений: топология, риманова геометрия, теория вероятности;

3) Рассмотреть новые области применения математики в XX веке;

4) Ознакомиться с использованием сведений о современном развитии математики в начальной школе.

 

 

Глава 1. Основные направления развития математики в XX веке.

 Особенное развитие в XX веке получили новые области математики; кроме компьютерных потребностей, это во многом связано с запросами теории управления, квантовой физики и других прикладных дисциплин.

· Топология.

· Функциональный анализ.

· Различные разделы дискретной математики, в том числе теория игр, теория графов, теория кодирования.

· Информатика и кибернетика, теория информации, теория алгоритмов.

· Теория групп Ли.

· Теория компьютерного моделирования.

· Теория оптимизации, в том числе глобальной.

· Теория случайных процессов.

· Методы математической статистики.

 Так же бурно развивались и многие «старые» области математики.

· Алгебраическая геометрия

· Комплексный анализ, особенно для функций многих переменных

· Математическая физика

· Общая алгебра

· Риманова геометрия

· Теория вероятностей [14]

 

Топология.

Топология - раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация – это деформация фигуры, при которой не происходит разрывов (т.е. нарушения целостности фигуры) или склеиваний (т.е. отождествления ее точек). Такие геометрические свойства связаны с положением, а не с формой или величиной фигуры. В отличие от евклидовой и римановой геометрий, геометрии Лобачевского и других геометрий, занимающихся измерением длин и углов, топология имеет неметрический и качественный характер. Раньше она носила названия «анализ ситус» (анализ положения), а также «теория точечных множеств». В научно-популярной литературе топологию часто называют «геометрией на резиновом листе», поскольку ее наглядно можно представлять себе как геометрию фигур, нарисованных на идеально упругих резиновых листах, которые подвергаются растяжению, сжатию или изгибанию. Топология – один из новейших разделов математики. [1]

История.

В 1640 французский философ и математик Р.Декарт (1596–1650) нашел инвариантное соотношение между числом вершин, ребер и граней простых многогранников. Это соотношение Декарт выразил формулой V – E + F = 2, где V – число вершин, E – число ребер и F – число граней. В 1752 швейцарский математик Л.Эйлер (1707–1783) дал строгое доказательство этой формулы. Еще один вклад Эйлера в развитие топологии – это решение знаменитой задачи о кёнигсбергских мостах. Речь шла об острове на реке Прегель в Кёнигсберге (в том месте, где река разделяется на два рукава – Старый и Новый Прегель) и семи мостах, соединяющих остров с берегами. Задача состояла в том, чтобы выяснить, можно ли обойти все семь мостов по непрерывному маршруту, побывав на каждом только один раз и вернувшись в исходную точку. Эйлер заменил участки суши точками, а мосты – линиями. Полученную конфигурацию Эйлер назвал графом, точки – его вершинами, а линии – ребрами. Вершины он разделил на четные и нечетные в зависимости от того, четное или нечетное число ребер выходит из вершины. Эйлер показал, что все ребра графа можно обойти ровна по одному разу по непрерывному замкнутому маршруту, лишь если граф содержит только четные вершины. Так как граф в задаче о кёнигсбергских мостах содержит только нечетные вершины, мосты невозможно обойти по непрерывному маршруту, побывав на каждом ровно по одному разу и вернувшись к началу маршрута. [12]

Предложенное Эйлером решение задачи о кенигсбергских мостах зависит только от взаимного расположения мостов. Оно положило формальное начало топологии как разделу математики. К.Гаусс (1777–1855) создал теорию узлов, которой позднее занимались И.Листинг (1808–1882), П.Тэйт (1831–1901) и Дж.Александер. В 1840 А.Мёбиус (1790–1868) сформулировал так называемую проблему четырех красок, которую впоследствии исследовали О.де Морган (1806–1871) и А.Кэли (1821–1895). Первым систематическим трудом по топологии были Предварительные исследования по топологии Листинга (1874). Основателями современной топологии являются Г.Кантор (1845–1918), А.Пуанкаре (1854–1912) и Л.Брауэр (1881–1966). [15]

Разделы топологии.

Топологию можно подразделить на три области: 1) комбинаторную топологию, изучающую геометрические формы посредством их разбиения на простейшие фигуры, регулярным образом примыкающие друг к другу; 2) алгебраическую топологию, занимающуюся изучением алгебраических структур, связанных с топологическими пространствами, с упором на теорию групп; 3) теоретико-множественную топологию, изучающую множества как скопления точек (в отличие от комбинаторных методов, представляющих объект как объединение более простых объектов) и описывающую множества в терминах таких топологических свойств, как открытость, замкнутость, связность и т.д. Разумеется, такое деление топологии на области в чем-то произвольно; многие топологи предпочитают выделять в ней другие разделы. [13]

Некоторые основные понятия.

Топологическое пространство состоит из множества точек S и набора S подмножеств множества S, удовлетворяющего следующим аксиомам:

(1) все множество S и пустое множество принадлежат набору S;

(2) объединение любой совокупности множеств из S есть множество из S;

(3) пересечение любого конечного числа множеств из S есть множество из S.

Множества, входящие в набор S, называются открытыми множествами, а сам этот набор – топологией в S. Топологическое преобразование, или гомеоморфизм, одной геометрической фигуры S на другую, Sў, – это отображение (p → pў) точек p из S в точки pў из Sў, удовлетворяющее следующим условиям: 1) устанавливаемое им соответствие между точками из S и Sў взаимно однозначно, т.е. каждой точке p из S соответствует только одна точка pў из Sў и в каждую точку pў отображается только одна точка p; 2) отображение взаимно непрерывно (непрерывно в обе стороны), т.е. если заданы две точки p, q из S и точка p движется так, что расстояние между ней и точкой q стремится к нулю, то расстояние между соответствующими точками pў, qў из Sў также стремится к нулю, и наоборот. [11]

Геометрические фигуры, переходящие одна в другую при топологических преобразованиях, называются гомеоморфными. Окружность и граница квадрата гомеоморфны, так как их можно перевести друг в друга топологическим преобразованием (т.е. изгибанием и растяжением без разрывов и склеиваний, например, растяжением границы квадрата на описанную вокруг него окружность). Сфера и поверхность куба также гомеоморфны. Чтобы доказать гомеоморфность фигур, достаточно указать соответствующее преобразование, но тот факт, что для каких-то фигур найти преобразование нам не удается, не доказывает, что эти фигуры не гомеоморфны. Здесь помогают топологические свойства. [15]

Рис. 1. ПОВЕРХНОСТЬ КУБА И СФЕРА гомеоморфны, т.е. могут быть переведены друг в друга топологическим преобразованием, но ни поверхность куба, ни сфера не гомеоморфны тору (поверхности «бублика»).       

                                                                               

                                                                                                  Рис.1.

Топологическим свойством (или топологическим инвариантом) геометрических фигур называется свойство, которым вместе с данной фигурой обладает также любая фигура, в которую она переходит при топологическом преобразовании. [1]

Любое открытое связное множество, содержащее по крайней мере одну точку, называется областью.

Область, в которой любую замкнутую простую (т.е. гомеоморфную окружности) кривую можно стянуть в точку, оставаясь все время в этой области, называется односвязной, а соответствующее свойство области – односвязностью. Если же некоторую замкнутую простую кривую этой области нельзя стянуть в точку, оставаясь все время в этой области, то область называется многосвязной, а соответствующее свойство области – многосвязностью. Представьте себе две круговые области, или диски, одну без дыр, а другую с дырами. Первая область односвязна, вторая многосвязна. Односвязность и многосвязность – топологические свойства. Область с дырой не может перейти при гомеоморфизме в область без дыр. Интересно отметить, что если в многосвязном диске провести по разрезу от каждой из дыр до края диска, то он станет односвязным. [13]

Максимальное число замкнутых простых непересекающихся кривых, по которым можно разрезать замкнутую поверхность, не разделяя ее на отдельные части, называется родом поверхности. Род – топологический инвариант поверхности. Можно доказать, что род сферы равен нулю, род тора (поверхности «бублика») – единице, род кренделя (тора с двумя дырками) – двум, род поверхности с p дырами равен p. Отсюда следует, что ни поверхность куба, ни сфера не гомеоморфны тору.

Среди топологических инвариантов поверхности можно также отметить число сторон и число краев. Диск имеет 2 стороны, 1 край и род 0. Тор имеет 2 стороны, не имеет краев, а его род равен 1.

Введенные выше понятия позволяют уточнить определение топологии: топологией называется раздел математики, изучающий свойства, которые сохраняются при гомеоморфизмах. [12]

Важные проблемы и результаты.

Теорема Жордана о замкнутой кривой.

Если на поверхности проведена простая замкнутая кривая, то существует ли какое-либо свойство кривой, которое сохраняется при деформации поверхности? Существование такого свойства вытекает из следующей теоремы: простая замкнутая кривая на плоскости делит плоскость на две области, внутреннюю и внешнюю. Эта кажущаяся тривиальной теорема очевидна для кривых простого вида, например, для окружности; однако для сложных замкнутых ломаных дело обстоит иначе. Теорема была впервые сформулирована и доказана К.Жорданом (1838–1922); однако доказательство Жордана оказалось ошибочным. Удовлетворительное доказательство было предложено О.Вебленом (1880–1960) в 1905. [15]

Теорема Брауэра о неподвижной точке.

Пусть D – замкнутая область, состоящая из окружности и ее внутренности. Теорема Брауэра утверждает, что для любого непрерывного преобразования, переводящего каждую точку области D в точку этой же области, существует некоторая точка, которая остается неподвижной при этом преобразовании. (Преобразование не предполагается взаимно однозначным.) Теорема Брауэра о неподвижной точке представляет особый интерес потому, что она, по-видимому, является, наиболее часто используемой в других разделах математики топологической теоремой. [1]

Проблема четырех красок.

Проблема заключается в следующем: можно ли любую карту раскрасить в четыре цвета так, чтобы любые две страны, имеющие общую границу, были раскрашены в различные цвета? Проблема четырех красок топологическая, так как ни форма стран, ни конфигурация границ не имеют значения.

Гипотеза о том, что четырех красок достаточно для соответствующей раскраски любой карты, была впервые высказана в 1852. Опыт показал, что четырех красок действительно достаточно, но строгого математического доказательства не удавалось получить на протяжении более ста лет. И только в 1976 К.Аппель и В.Хакен из Иллинойского университета, затратив более 1000 часов компьютерного времени, добились успеха.

Односторонние поверхности.

Простейшей односторонней поверхностью является лист Мёбиуса, названный так в честь А.Мёбиуса, открывшего его необычайные топологические свойства в 1858. Пусть ABCD (рис. 2,а) – прямоугольная полоска бумаги. Если склеить точку A с точкой B, а точку C с точкой D (рис. 2,б), то получится кольцо с внутренней поверхностью, наружной поверхностью и двумя краями. Одну сторону кольца (рис. 2,б) можно окрасить. Окрашенная поверхность будет ограничена краями кольца. Жук может совершить «кругосветное путешествие» по кольцу, оставаясь либо на окрашенной, либо на неокрашенной поверхности. Но если полоску перед склеиванием концов перекрутить на полоборота и склеить точку A с точкой C, а B с D, то получится лист Мёбиуса (рис. 2,в). У этой фигуры есть только одна поверхность и один край. Любая попытка окрасить только одну сторону листа Мёбиуса обречена на неудачу, так как у листа Мёбиуса всего одна сторона. Жук, ползущий по середине листа Мёбиуса (не пересекая края), вернется в исходную точку в положении «вверх ногами». При разрезании листа Мёбиуса по средней линии он не распадается на две части. [6]

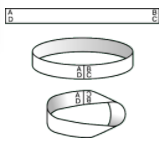Рис. 2. СКЛЕЕННАЯ В КОЛЬЦО ПОЛОСКА (б) имеет внутреннюю и внешнюю стороны и два края. Лист Мёбиуса (в), склеенный из перекрученной на полоборота прямоугольной полоски (а), имеет только одну сторону и один край.     

                                                                                                   Рис.2.                                                                                                                                                                                                                   

Узлы.

Узел можно представлять себе как запутанный кусок тонкой веревки с соединенными концами, расположенный в пространстве. Простейший пример – из куска веревки сделать петлю, пропустить один из ее концов сквозь петлю и соединить концы. В результате мы получим замкнутую кривую, которая остается топологически той же самой, как бы ее ни растягивать или скручивать, не разрывая и не склеивая при этом отдельные точки. Проблема классификации узлов по системе топологических инвариантов пока не решена.

Риманова геометрия.

РИ́МАНОВА ГЕОМЕ́ТРИЯ, мно­го­мер­ное обоб­ще­ние гео­мет­рии на по­верх­но­сти, пред­став­ляю­щее со­бой тео­рию ри­ма­но­вых про­странств, т. е. та­ких про­странств, где в ма­лых об­лас­тях при­бли­жён­но име­ет ме­сто евк­ли­до­ва гео­мет­рия (с точ­но­стью до ма­лых выс­ше­го по­ряд­ка по срав­не­нию с раз­ме­ром об­лас­ти). Р. г. по­лу­чи­ла своё назв. по име­ни Б. Ри­ма­на, за­ло­жив­ше­го её ос­но­вы в 1854. [3]

Научно-исследовательские труды Бернхард Римана оказали огромное влияние на развитие математики в конце XIX и начале XX веков.
Выдающийся математик и геометр Риман ввел так называемые римановы поверхности, которые сыграли важную роль при исследовании многозначных функций. В 1854 году в своей знаменитой лекции «О гипотезах, лежащих в основании геометрии» Риман дал общую идею математического пространства или «многообразия», включая функциональные и топологические пространства. Здесь Риман рассматривал геометрию как учение о непрерывных n-мерных многообразиях, то есть совокупностях любых однородных объектов. Обобщив результаты К. Гаусса по внутренней геометрии поверхностей, Риман сформулировал понятие линейного элемента, так называемого дифференциала расстояния между точками многообразия. Главным достижением ученого Римана стало создание новой геометрии.Риманова геометрия — это раздел дифференциальной геометрии, объектом изучения которой, главным образом, являются римановы многообразия. Римановы многообразия — это гладкие многообразия с дополнительной структурой, римановой метрикой, то есть с выбором евклидовой метрики на каждом касательном пространстве, которая гладко меняется от точки к точке. Подразделом римановой геометрии является геометрия в целом, которая выявляет связь глобальных свойств риманова многообразия (к примеру, топология или диаметр) и его локальных свойств (к примеру, ограничений на кривизну).Основными элементами трехмерной римановой геометрии являются точки, прямые и плоскости.В римановой геометрии имеют место такие предложения: через каждые две точки проходит одна прямая, каждые две плоскости пересекаются по одной прямой, каждые две прямые, лежащие в одной плоскости, пересекаются (в одной точке), точки на прямой расположены в циклическом порядке (как и прямые, лежащие в одной плоскости и проходящие через одну точку). Таким образом, требования аксиом римановой геометрии, относящиеся конгруэнтности, обеспечивают свободные движения фигур по плоскости и в пространстве Римана, как на плоскости, так и в пространстве Евклида.Метрические свойства плоскости Римана «в малом» совпадают с метрическими свойствами обыкновенной сферы, а именно: для любой точки плоскости Римана существует содержащая эту точку часть плоскости, изометричная некоторой части сферы; радиус R этой сферы — один и тот же для всех плоскостей данного пространства Римана. Число К = 1/R2 называется кривизной пространства Римана. Следует отметить, что, чем меньше К, тем ближе свойства фигур этого пространства к евклидовым.«В целом» свойства плоскости Римана отличаются от свойств целой сферы в следующем: на плоскости Римана две прямые пересекаются в одной точке, а на сфере два больших круга, которые выступают как прямые в сферической геометрии, пересекаются в двух точках; прямая, лежащая на плоскости, не разделяет эту плоскость, таким образом, если прямая а лежит в плоскости a, то любые две точки плоскости a, не лежащие на прямой а, возможно соединить отрезком, не пересекая прямой а.Таким образом, Риман построил вторую разновидность неевклидовой геометрии в противоположность геометрии Лобачевского.Уникальные идеи и методы, предложенные Риманом открыли новые пути для развития математики и нашли применение в механике и физике. Развитию римановой геометрии послужило создание итальянскими учеными Риччи-Курбастро и Леви-Чивита тензорного исчисления. [8]

В евклидовой геометрии, как и в гиперболической геометрии Бойаи - Лобачевского, молчаливо допускается, что всякая прямая бесконечна (бесконечность прямой существенно связана с отношением "быть между" и аксиомами порядка). Но после того как гиперболическая геометрия открыла путь к свободному построению геометрий, естественно возник вопрос о том, нельзя ли осуществить построение таких неевклидовых геометрий, в которых прямые линии конечны и замкнуты. Разумеется, в таких геометриях теряют силу не только постулат о параллельных, но и аксиомы порядка. Современные исследования выяснили значение этих геометрий для новейших физических теорий. Впервые такие геометрии были подвергнуты рассмотрению в речи, произнесенной в 1851 г. Риманом при вступлении его в должность приват-доцента Гёттингенского университета. Геометрии с замкнутыми конечными прямыми могут быть построены без каких бы то ни было противоречий Вообразим двумерный мир, состоящий из поверхности S сферы, причем под "прямыми" условимся понимать большие круги сферы. Это был бы самый естественный способ описывать "мир" мореплавателя: дуги больших кругов являются кратчайшими кривыми, связывающими две точки на сфере, а это как раз и есть характеристическое свойство прямых на плоскости. В рассматриваемом двумерном мире всякие две "прямые" пересекаются, так что из внешней точки нельзя провести ни одной "прямой", не пересекающейся с данной (т. е. ей параллельной). Геометрия "прямых" в этом мире называется эллиптической геометрией. Расстояние между двумя точками в такой геометрии измеряется просто как длина кратчайшей дуги большого круга, проходящего через данные точки. Углы измеряются так же, как и в евклидовой геометрии. Самым характерным свойством эллиптической геометрии мы считаем несуществование параллельных. [3]

 

 

 

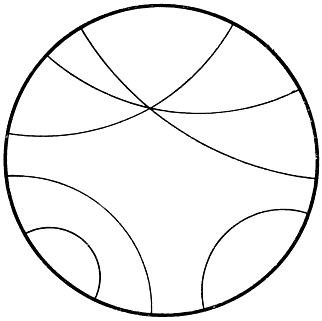
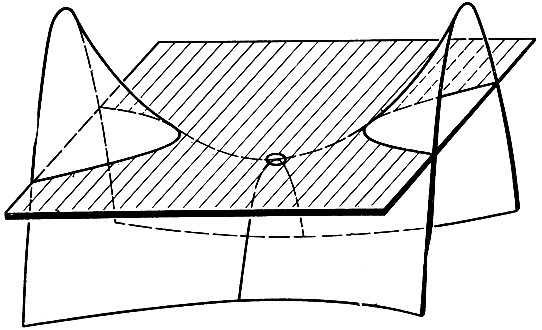
           Рис. 3 Модель неевклидовой плоскости Пуанкаре.

 
Следуя Риману, мы можем обобщить эту геометрию следующим образом. Рассмотрим "мир", состоящий из некоторой кривой поверхности в пространстве (не обязательно сферы) и определим "прямую линию", проходящую через две точки, как кратчайшую кривую ("геодезическую"), соединяющую эти точки. Точки поверхности можно разбить на два класса: 1°. Точки, в окрестности которых поверхность подобна сфере в том отношении, что она вся лежит по одну сторону от касательной плоскости в этой точке. 2°. Точки, в окрестности которых поверхность седлообразна (лежит по обе стороны касательной плоскости). Точки первого класса называются эллиптическими точками поверхности - по той причине, что при небольшом параллельном перемещении касательной плоскости она пересечет поверхность по кривой, имеющей вид эллипса; точки же второго класса носят название гиперболических, так как при аналогичном перемещении касательной плоскости получается пересечение с поверхностью, напоминающее гиперболу. Геометрия геодезических "прямых" в окрестности точки поверхности является эллиптической или гиперболической, смотря по тому, будет ли сама точка эллиптической или гиперболической. На этой модели неевклидовой геометрии углы измеряются, как в обыкновенной евклидовой геометрии.

 

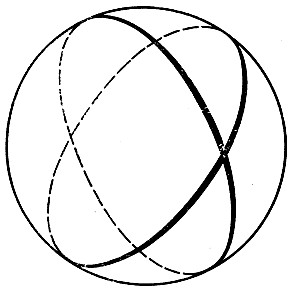
Рис.4. 'Прямые линии' в геометрии Римана

Изложенная идея была развита Риманом дальше: он рассмотрел геометрии пространства, аналогичные только что разобранным геометриям поверхности. По Риману, "кривизна" пространства, меняясь от точки к точке, определяет характер геометрии в окрестности точки. "Прямые линии" у Римана - геодезические кривые. В эйнштейновой общей теории относительности геометрия пространства есть риманова геометрия; свет распространяется по геодезическим линиям, а кривизна пространства в каждой точке определяется в зависимости от свойств материи в окрестности точки.[3]

 

Рис. 5. Эллиптическая точка

Возникнув из чисто аксиоматических изысканий, неевклидова геометрия в наши дни стала чрезвычайно полезным аппаратом, допускающим различные применения при изучении физической реальности. В теории относительности, в оптике, в общей теории колебаний неевклидово описание явлений оказывается в ряде случаев гораздо более адекватным физической реальности, чем евклидово.[3]

 

Рис. 6. Гиперболическая точка

Теория вероятности.

Тео́рия вероя́тностей — раздел математики, изучающий: случайные события, случайные величины, их свойства и операции над ними.[4]

Историки выделяют в развитии теории вероятностей несколько периодов.

Предыстория, до XVI века включительно. В античные времена и в Средневековье натурфилософы ограничивались метафизическими рассуждениями о происхождении случайности и её роли в природе. Математики в этот период рассматривали и иногда решали задачи, связанные с теорией вероятностей, но никаких общих методов и тематических понятий ещё не появилось. Главным достижением данного периода можно считать развитие комбинаторных методов, которые позже пригодились создателям теории вероятностей. [10]

Начало формирования во второй половине XVII века основных понятий и методов теории вероятностей для случайных величин с конечным числом значений. Стимулом вначале служили преимущественно проблемы, возникающие в азартных играх, однако область применения теории вероятностей почти сразу начинает расширяться, включая в себя прикладные задачи демографической статистики, страхового дела и теории приближённых вычислений. На этом этапе важный вклад в идеи новой науки внесли Паскаль и Ферма. Гюйгенс ввёл два фундаментальных понятия: числовая мера вероятности события, а также понятие математического ожидания случайной величины.

В XVIII веке появились монографии с систематическим изложением теории вероятностей. Первой из них стала книга Якоба Бернулли «Искусство предположений» (1713 год). В ней Бернулли предложил классическое определение вероятности случайного события как отношение числа равновероятных исходов, связанных с этим событием, к общему числу исходов. Он также изложил правила подсчёта вероятности для сложных событий и дал первый вариант ключевого «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности). [7]

Идеи Бернулли далеко развили в начале XIX века Лаплас, Гаусс, Пуассон. Применение вероятностных методов в прикладной статистике значительно расширилось. Понятие вероятности стало определено и для непрерывных случайных величин, благодаря чему появилась возможность применения методов математического анализа. Появляются первые попытки применения теории вероятностей в физике. К концу XIX века появляются статистическая физика, строгая теория ошибок измерения, вероятностные методы проникают в самые различные прикладные науки. [11]

В XX веке в физике была создана теория микромира, а в биологии — теория наследственности, обе они существенно основаны на вероятностных методах. Карл Пирсон разработал алгоритмы математической статистики, широко и повсеместно применяемые для анализа прикладных измерений, проверки гипотез и принятия решений. А. Н. Колмогоров дал классическую аксиоматику теории вероятностей. Из других новых областей применений теории вероятностей необходимо упомянуть теорию информации и теорию случайных процессов. Философские споры о том, что такое вероятность и в чём причина её устойчивости, продолжаются.

История теории вероятностей отмечена многими уникальными особенностями. Прежде всего, в отличие от появившихся примерно в то же время других разделов математики (например, математического анализа или аналитической геометрии), у теории вероятностей по существу не было античных или средневековых предшественников, она целиком — создание Нового времени. Долгое время теория вероятностей считалась чисто опытной наукой и «не совсем математикой», её строгое обоснование было разработано только в 1929 году, то есть даже позже, чем аксиоматика теории множеств (1922). В наши дни теория вероятностей занимает одно из первых мест в прикладных науках по широте своей области применения; «нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы»[10]

В XX веке исследования Чебышёва и Маркова продолжили А. Я. Хинчин, А. Н. Колмогоров и др. В частности, Ярл В. Линдеберг (1922) и Колмогоров (1926) нашли условия, необходимые и достаточные для выполнения закона больших чисел.

Математический аппарат теории вероятностей значительно обогатился во многих направлениях. После разработки теории меры это общее понятие оказалось удобно применить к теории вероятностей, то есть рассматривать вероятность как меру (конечного или бесконечного) множества «благоприятных событий». Такой подход позволяет описывать и исследовать свойства вероятности на хорошо разработанном языке теории множеств

В теории динамических систем было обнаружено, что решения дифференциальных уравнений некоторых систем ведут себя как случайные процессы. Это крупное открытие привело к созданию понятия «динамический хаос» и общей «теории хаоса». Одним из примеров является «задача трёх тел» небесной механики.[7]

До XX века использовались в основном нормальное, биномиальное и (иногда) пуассоновское распределения, однако практически полезными оказались и многие другие теоретические законы. Например, логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных величиц.

Вероятностные методы оказались плодотворными во многих областях теоретической и прикладной математики, даже в таких классических, как теория чисел или логика. В свою очередь, современная теория вероятностей использует методы и подходы, разработанные в функциональном анализе, топологии и других разделах математики, появившихся в XX веке. [10]

Новые применения вероятностных методов возникали в XX веке постоянно и во многих науках; кратко перечислим некоторые этапные события в этой тенденции.

Физика

Центральным понятием созданной в 1920-е годы квантовой механики является комплексная волновая функция, квадрат модуля которой, согласно распространённой копенгагенской интерпретации, определяет плотность вероятности обнаружения микрочастицы в данной точке пространства. Если принять такую интерпретацию, то в математической модели микромира случайность неустранима, а лапласовский детерминизм полностью опровергнут. Для микромира были разработаны специальные квантовые статистики Бозе — Эйнштейна и Ферми — Дирака. [4]

Биология

После открытий Менделя и Моргана стало понятно, что наследственные признаки передаются потомкам путём случайной комбинации одного из двух признаков (аллелей) от отца и одного из двух аналогичных аллелей от матери. Случайный выбор аллели отца определяет заодно пол будущего потомка. На этот процесс дополнительно накладываются случайные мутации, поэтому вероятностные методы легли в основу генетики. Применяются они также при исследовании и управлении развитием биологических популяций. Существенно используются вероятностные подходы (например, байесовские методы и методы, основанные на принципе наибольшего правдоподобия) в вычислительной филогенетике, предусматривающей применение специальных вычислительных алгоритмов и компьютерных программ для построения филогенетических деревьев. [4]

Кибернетика и теория информации

Теория информации опирается на введённое Клодом Шенноном в 1948 году понятие информационной энтропии. Если случайная величина x может принимать значения , ,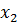…  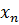вероятности которых соответственно равны 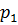, , 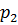…, , 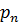то энтропия определяется формулой:

                         .

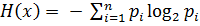Определённая так энтропия есть мера случайности (или неопределённости): она равна нулю, если случайность отсутствует, то есть с вероятностью 1 величина принимает одно определённое значение. Увеличение случайности связано с увеличением энтропии.

Теория автоматического управления также изначально использовала вероятностные методы. С появлением компьютеров применение таких методов многократно расширилось. Используя генератор псевдослучайных чисел, можно промоделировать на компьютере случайные величины или процессы с произвольным распределением, а это, в свою очередь, позволяет исследовать самые разные реальные процессы путём их компьютерного моделирования (метод Монте-Карло). [10]

Лингвистика

Во 2-й половине XX века в важное направление математической лингвистики оформилось применение методов теории вероятностей и математической статистики к изучению лингвистических явлений. Многочисленные исследования, основанные на применении таких методов, включали: получение вероятностно-информационных оценок нормы языка; анализ распределения синтаксической информации в пределах словоформы, контекстной обусловленности и избыточности текстов, взаимодействия случайных и детерминированных процессов в речи; разработку адекватных методик лингвистического эксперимента; выявление статистических характеристик лингвистических вариационных рядов и др.

Обоснование и аксиоматизация

К моменту создания теории вероятностей основой математики были два класса объектов — числа и геометрические фигуры. Для теории вероятностей потребовалось добавить в этот список совершенно особый объект: случайное событие, а также тесно связанные с ним понятия (вероятность, случайная величина и др.). Своеобразие новой науки проявлялось и в том, что её утверждения носили не безусловный характер, как ранее было принято в математике, а предположительно-вероятностный.

По мере развития теории вероятностей не прекращались споры о том, можно ли считать идеализированное событие математическим понятием (и тогда теория вероятностей есть часть математики) или же это факт, наблюдаемый в опыте (и тогда теорию вероятностей следует отнести к естественным наукам). Разные учёные высказывали самые разные мнения на этот счёт. П. Л. Чебышёв уверенно считал теорию вероятностей математической дисциплиной, задача которой — по известным вероятностям некоторых событий определить неизвестную вероятность исследуемого события. По мнению Давида Гильберта, теория вероятностей родственна механике, то есть представляет собой математизированную «физическую дисциплину». Август де Морган и его последователь У. С. Джевонс считали базовым понятием «субъективную вероятность», то есть количественную меру нашего понимания предмета исследования, и связывали теорию вероятностей с логикой. Проблемы, связанные с неоднозначной субъективной вероятностью, неоднократно обсуждались, их часто формулируют в виде «вероятностных парадоксов» (см., например, «парадокс трёх узников» или «парадокс мальчика и девочки»). [4]

Ещё Бернулли дал фактически два определения вероятности: как доли «благоприятных случаев» и как статистической частоты; чтобы свести второе понимание к первому, понадобился закон больших чисел. Австрийский математик и механик Рихард фон Мизес предложил обратный подход (1914 год): считать определением вероятности именно предел частоты. Теорию вероятностей Мизес к математике не относил, он считал её опытной наукой, изучающей наблюдаемые факты. Определение Мизеса и изложенная им аксиоматика подверглись критике за бессодержательность, поскольку не существует средств для выяснения, имеет ли частота заданного события предел. Обсуждение концепции Мизеса иногда продолжается и в наши дни. Были и другие попытки обоснования — Джон Мейнард Кейнс (1921) и Гарольд Джеффрис (1939) предложили понимать вероятность утверждения как «степень правдоподобия» этого утверждения, этот подход также время от времени упоминается в обсуждении вопроса..[4]

В начале XX века школа Д. Гильберта поставила такие классические разделы математики, как геометрия и анализ, на строгую аксиоматическую основу, появилась аксиоматика и в других разделах математики: теория множеств, математическая логика и др. Назрела необходимость разработать аксиоматику и для теории вероятностей, поскольку старое, полуинтуитивное и неформальное обоснование Бернулли и Лапласа давно устарело. Первый вариант такой аксиоматики дал советский математик С. Н. Бернштейн в своём курсе «Теория вероятностей» (1927 год). Общепризнанным в науке стал вариант А. Н. Колмогорова, опубликованный в 1929—1933 годах и основанный на идеях теории меры. Во второй половине XX века Альфред Реньи и А. Н. Колмогоров исследовали возможность дать обоснование теории вероятностей на базе теории информации. В наши дни «сложилось чёткое понимание того, что теория вероятностей является подлинно математической наукой, имеющей вместе с тем самые тесные и непосредственные связи с широким спектром наук о природе, а также с техническими и социально-экономическими дисциплинами» [10]

Раскрыв выбранные направления, можно сделать вывод, что развитие математики XX века играет большую роль в развитии математики и геометрии последующих эпох. На данном этапе математика раскрывается глубже, так как ученые уже на имеющихся знаниях строят, развивают и доказывают свои открытия, законы, разработки и т.д. Яркими примерами являются Б.Риман, А.Мёбиус, А.Н. Колмогоров. Развитие математики XX века внесло огромный вклад в развитие современных технологий.

 

 

Глава 2. Новые области применения математики в XX веке.