Для нахождения кратчайшего расстояния и соответственно кратчайшей цепи между двумя заданными вершинами в графе может использоваться алгоритм Дэйкстры.
В данном алгоритме каждой из вершин в соответствие ставится метка - число, равное наименьшему известному расстоянию от данной вершины до начальной вершины. На каждом шаге алгоритм посещает одну из вершин и пытается уменьшить метки. Работа алгоритма завершается, когда все вершины посещены. Для простейшего случая реализации, когда для поиска вершины с минимальной меткой просматривается все множество вершин, сложность работы алгоритма составляет 
, где n-количество вершин, m- количество рёбер.
Раскраска графов.
Задачи раскраски графа сводятся к назначению каждой из вершин определённого цвета, так, чтобы любые две смежные вершины были окрашены в разные цвета. На практике с помощью методов раскраски графа решаются задачи составления расписания, распределения радиочастот и прочих подобных задачах.
Хроматическое число графа — минимальное число цветов, в которые можно раскрасить вершины графа так, чтобы концы любого ребра имели разные цвета.
Задача раскраски произвольного графа минимальным числом цветов относится к категории NP-полных задач. Обычно решение сводится к перебору всех возможных вариантов.
Рассмотрим следующий алгоритм. Цвет будет задаваться переменной color и для каждой вершины сохраняться в массиве c[]. Q – очередь ещё не раскрашенных вершин.
добавим в очередь Q все вершины;
while(пока очередь Q не пуста)
{
color=color+1;
for(для каждой вершины 
)
{
for(для каждой вершины v, смежной u)
{
if(c[v]==color) nextColor=true;
}
if(nextColor==false)
{
c[u]=color;
удалить u из очереди Q;
}
}
}
Алгоритм пытается раскрасить как можно больше вершин в первый цвет, затем как можно больше вершин во второй цвет. И так далее, до того момента, когда все вершины будут раскрашены. Алгоритмы подобного вида называются жадными. Они принимают локально наилучшее решение на каждом этапе своей работы, считая при этом, что конечное решение также будет оптимальным и наилучшим.
Алгоритмы решения задач вычислительной математики.
У множение матриц.
Пусть заданы две матрицы размерности 
и 
.
, 
Матрица С размерностью 
называется их произведением:
, если
Псевдокод алгоритма перемножения:
Ввод матриц A[m][n]; B[n][q];
for(int i=0; i<m; i++)
{
for(int j=0; j<q; j++)
{
for(int k=0; k<n; k++)
{
C[i][j]=C[i][j]+A[i][k]*B[k][j];
}
}
}
Результат сохраняется в матрице C[n][q];
Сложность алгоритма будет составлять 
;
Метод Гаусса.
Метод Гаусса используется для решения систем линейных алгебраических уравнений. Основная идея метода в последовательном исключении переменных с помощью элементарных преобразований и приведения к равносильной системе ступенчатого или треугольного вида.
Пусть задана ситема:
Алгоритм нахождения решений делится на два этапа: прямой и обратный ход. При прямом ходе систему приводят к треугольной форме. Выбирается ведущий элемент как первый не нулевой элемент первого столбца. Далее происходит исключение переменной при ведущем элементе из последующих строк путём вычитания:
В течение обратного хода находятся значения всех неизвестных:
Данный алгоритм не применим при равенстве нулю хотя бы одного из ведущих элементов. Также при малых значениях ведущего элемента увеличиваются ошибки округления и снижению точности полученного значения.
Для преодоления данных недостатков используют алгоритм Гаусса с выбором главного элемента. В данном алгоритме в качестве ведущего элемента выбирается максимальный по модулю коэффициент aij. По правилам перестроения строк и столбцов aij переставляется на место элемента a11 и далее вычисление осуществляется подобно простому алгоритму Гаусса.
Метод LU-разложения.
Пусть задана система уравнений
Такую систему можно записать в матричной форме: 
, где
, 
, 
LU разложением называется разложение вида: 
, где 
Решение системы можно последовательно получить последовательным решением систем:
и 
Матрица U – верхнетреугольная, матрица L-нижнетреугольная.
Для нахождения элементов каждой из матриц используются следующие шаги:
диагональные элементы матрицы L 
, при i =1..n
Для i =2..n
После нахождения L и U матриц уравнения и решаются при помощи обычных подстановок обратного хода метода Гаусса. Сложность при решении уравнения методом Гаусса и методом LU разложения одинакова, однако при последовательном решении уравнений с одинаковыми матрицами A, но разными коэффициентами b LU-разложение оказывается предпочтительнее, так как A не меняется и нет затрат на повторное разложение.
Метод простой итерации.
При большом числе уравнений прямые методы решения систем линейных уравнений становятся труднореализуемыми из-за сложности хранения и обработки матриц большой размерности, более часто используют итерационные методы.
Методы последовательных приближений, в которых при вычислении последующего приближения решения используются предыдущие, уже известные приближенные решения, называются итерационными.
Пусть задана система уравнений:
преобразуем её к виду:
, где 
, 
Если обозначить
и 
, то систему можно записать в матричной форме: 
Любые k-тые приближения X вычисляются по формуле: 
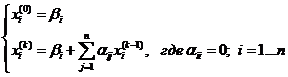
Процесс итерации для линейной системы сходится к единственному её решению, если какая-нибудь каноническая норма матрицы A меньше единицы.
m -норма матрицы: 
l -норма матрицы: 
k-норма матрицы (Евклидова норма) 
Условием окончания итерационного процесса нахождения корней системы является выполнение неравенства:
, где 
- заданная точность вычисления.
Метод Зейделя.
Модификацией метода итераций является метод Зейделя. В данном методе для вычисления k-й итерации корня xi(k) используются уже вычисленные ранее корни
x1(k)…xi-1(k)
Корни при начальной итерации обычно выбираются 
… 
.
К-тое приближение будет определяться формулами:
Условие окончания процесса итерации выбирается аналогично предыдущему методу.
ЛИТЕРАТУРА.
1. Кнут Д. Искусство программирования для ЭВМ. Т. 1. Основные алгоритмы. Пер. с англ. М.: Мир, 2000. – 720 c.
2. Кнут Д. Искусство программирования для ЭВМ. Т. 2. Получисленные алгоритмы. Пер. с англ. М.: Мир, 2000. – 832 c.
3. Кнут Д. Искусство программирования для ЭВМ. Т. 3. Сортировка и поиск. Пер. с англ. М.: Мир, 2000. – 824 c.
4. Матрос Д.Ш., Поднебесова Г. Б. Теория алгоритмов. М.: Бином. Лаборатория знания, 2008. – 208c.
5. Миллер Р., Боксер Л. Последовательные и параллельные алгоритмы: общий подход. М.: Бином. Лаборатория знания, 2006. – 406 c.
6. Новиков Ф.А. Дискретная математика для программистов. Учебник для вузов. 2-е изд.-СПб.: Питер, 2000. – 301 c.
7. Кинг Д. Создание эффективного программного обеспечения. - М.: Мир, 1991. - 367с.
8. Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1978. - 432c.
