Рассмотрим несколько алгоритмов, которые применяются в задачах конструкторского и технологического проектирования.
Задачи сортировки.
Сортировка пузырьком.
При такой сортировке выполняются повторяющиеся проходы по массиву. Элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются N-1 раз.
На входе массив A, состоящий из элементов A[1], A[2],..., A[n]
for (i:=1; i <= N-1; i++) {
for(j:=1; j <= N-i; j++)
{
if(A[j] > A[j+1])
{
Temp:=A[j];
A[j]:=A[j+1];
A[j+1]:=Temp;
}
}
}
Сложность алгоритма составляет O(n2).
Сортировка вставками.
На каждом шаге алгоритма выбирается один из элементов входных данных и вставляется на нужную позицию в уже отсортированном списке, до тех пор, пока набор входных данных не будет исчерпан. Отсортированная последовательность записывается в начало массива.
На входе массив A, состоящий из элементов A[1], A[2],..., A[n] for (i:=2; i <= n; i++)
{ key:= A[i]; j:= i – 1; while(j >= 1) { if(A[j] > key) { A[j + 1]:= A[j]; A[j]:= key; } j:= j – 1; }} 
Сложность алгоритма измеряется числом сравнений. Наилучший случай – когда исходный список уже отсортирован. Общее число сравнений равно n-1, т.е. сложность составляет O(n).
Наихудший случай возникает, когда список отсортирован по убыванию. Тогда каждая вставка происходит в точке A[0], и требует i сравнений. Общее число сравнений (вычисляется как сумма n членов арифметической прогрессии 
) 
. Сложность алгоритма составляет O(n2).
Сортировка слиянием.
Задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова.
Предполагает решение задач:
1. разбивания на две части примерно одинакового размера;
2. сортировки с использованием рекурсивного вызова;
3. объединения упорядоченных массивов половинного размера в один.
Для оценки времени работы данного рекурсивного алгоритма используем основную теорему о рекуррентных соотношения:
Пусть время работы алгоритма удовлетворяет соотношению 
, т.е. алгоритм делает a рекурсивных вызовов для подзадач размером 
, и тратит на подготовку к рекурсии и операции после завершения рекурсии 
времени.
Тогда 
Для алгоритма сортировки слиянием 
, так как производится два рекурсивных вызова с размером задачи равной половине от исходной.
Сложность алгоритма 
.
Например рассмотрим массив:
Сортировка с помощью кучи.
Пусть задан массив. Представим его как бинарное дерево:
Преобразуем данное дерево в кучу. В куче значение в любой вершине не меньше чем значение её потомков. В листьях условие кучи выполняется. Если в каой-либо вершине условие не выполняется значение вершины меняется на максимальное из значений потомков.
После построения кучи можно сказать, что корневой элемент является максимальным в массиве. Поменяем его с последним элементом и уменьшим кучу на единицу:
Далее возможна ситуация, в которой нарушается свойство кучи, следовательно необходима перестройка структуры. Эта перестройка выполнится за время не боле log(n). Алгоритм завершается, когда в куче остаётся последний элемент. Сложность алгоритма 
.
Быстрая сортировка.
Пусть задан массив размера n. В массиве выберем опорный элемент x (который иногда называют разделитель). Далее переместим x на ту позицию, которую он занимал бы в отсортированном массиве. Другими словами все элементы массива слева от x меньше или равны ему, все элементы справа от x больше:
В левой и правой части элементы располагаются произвольным образом, отсортируем их, используя рекурсию.
Тело программы будет следующим:
QuickSort(A[], l, r)
{
if(l ≥ r) return;
m=Partition(A[], l, r);
QuickSort(A[], l, m-1);
QuickSort(A[], m+1, r);
}
Partition – функция, которая некоторым образом выбирает опорный элемент, ставит его на необходимую позицию в данном массиве и возвращает его новый индекс.
Partition(A[], l, r)
{
i:= l-1;
for(j= l; j ≤ r; j=j+1)
{
if(A[j] ≤ A[r])
{
temp:= A[i+1];
A[i+1]:= A[j];
A[j]:= temp;
i:= i+1;
}
}
return i;
}
В отличие от сортировки слиянием заранее не известно на какие части опорный элемент разобьет массив. Худшим случаем будет тот, когда в качестве опорного элемента будет всегда выбираться максимальный элемент. Тогда время работы алгоритма:
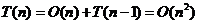
В случае, если в качестве опорного элемента будет выбираться элемент из середины отсортированного массива (медиана), то он будет делить массив примерно пополам и время работы будет: 
Для уменьшения времени работы и снижения вероятности плохого выбора опорного элемента, его выбирают случайным образом. Алгоритм называется вероятностным, если при своей работе он использует случайные числа. Время работы такого алгоритма оценивается его мат. ожиданием. Для улучшенного алгоритма быстрой сортировки .
