Параллельным называется соединение, когда от одной точки электрической схемы до другой ток может пройти несколькими путями (рис. 16). Левая и правая схемы, показанные на рисунке, абсолютно идентичны. Отличаются они только тем, что по разному нарисованы. На обеих схемах резисторы R1,R2, и R3 включены (соединены) параллельно.
Узлом называется точка электрической схемы, где сходится три или более проводов. На рисунке, для наглядности, узлы выделены окружностью (на левой схеме) и эллипсом (на правом). Каждая схема имеет по два узла. На схеме узел обозначается жирной точкой.
Может показаться, что на правой схеме узлов больше, чем два. Однако, это не так. На правой схеме точки 1, 2 и 3 – это разные геометрические точки. Но, для электротехники эти точки являются одной электрической точкой, одним узлом. Это объясняется тем, что точки 1, 2 и 3 соединены между собой проводником, сопротивление которого близко к нулю. Следовательно, все они имеют одини тот же потенциал и образуют одну общую точку. Из сказанного следует, что узел на схеме не всегда выглядит как геометрическая точка.
Ветвью называется участок схемы от узла до узла. В обеих схемах по три параллельные ветви. Разумеется, в других схемах их может быть больше.
Рис. 16. Параллельное соединение резисторов
Из рассмотрения схемы ясно, что на все резисторы поступает одинаковое напряжение U. В этом состоит главное свойство параллельного соединения элементов.
U1 = U2 = U3 = U
т.е. напряжение на каждом из резисторов равно напряжению,подаваемое на всю схему.
Как известно, напряжение в бытовой электросети составляет 220В. На такое напряжение рассчитаны все бытовые электроприборы. Чтобы напряжение на всех потребителях электроэнергии в квартире было одинаковым, все приёмники электроэнергии (телевизор, лампы, холодильник и др.) соединены параллельно.
Главным достоинством параллельного соединения элементов является то, что все они работают независимо друг от друга. В самом деле: мы по собственному опыту знаем, что включение телевизора не отражается на работе осветительных ламп, холодильника или других электроприборов, работающих в квартире.
Рассмотрим протекание токов в схеме. Направления токов показаны на схеме стрелками. К верхнему, по схеме, узлу подтекает общий ток всех потребителей. В узле он расходится по трём ветвям (движется по трём параллельным путям). В нижнем узле три тока вновь сливаются в один общий ток.
Для узлов электрической схемы справедлив первый закон Кирхгофа: сумма токов подходящих к узлу равна сумме токов отходящих от узла.
Закон Кирхгофа легко понять, представив вместо тока воду, текущую по трубам. Сначала вода идет по общей трубе. Затем труба разветвляется на три трубы идущие параллельно. Потом вода из трёх труб снова сливается в общий поток.
Токи в ветвях схемы вычисляются по формулам:
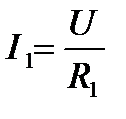
Эти токи могут быть равны, если все резисторы одинаковы. В противном случае токи будут различны по величине. В б о льшем сопротивлении будет протекать меньший ток и наоборот.
Изменение одного из сопротивлений вызовет изменение тока в этой ветви. Токи в других ветвях не изменятся. Общий ток, равный сумме всех токов, изменится.
Общее сопротивление цепи (всех резисторов, включённых параллельно) меньше наименьшего из сопротивлений, входящих в параллельную цепь.
Чем больше параллельных участков, тем меньше общее сопротивление, т.к. при большем количестве параллельных путей току легче протекать.
Общее сопротивление для двух резисторов, включённых параллельно, определяется по формуле:
Если резисторов три, то сначала определяется сопротивление двух из них, затем, используя ту же формулу, определяется сопротивление резисторов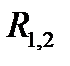 
и R3 (см. пример 8).
Пример 8. Расчёт цепи при параллельном соединении потребителей
В схеме, показанной на рис. 16, параллельно включены резисторы: R1= 20 Ом. R2= 30 Ом и R3 = 60 Ом. Напряжение, приложенное ко входу цепи U = 120 В.
Определить:
а) токи в ветвях и общий ток;
б) эквивалентное (общее) сопротивление цепи;
в) мощность, потребляемую каждым резистором и общую мощность цепи;
г) общий ток, I1 и I2 после отключения приемника R1.
Решение:
а) Напряжение U на всех ветвях (резисторах) при параллельном соединении одинаково. Находим токи в ветвях:
I1 = U / R1= 120 / 20 = 6 А,
I2 = U / R2= 120 / 30= 4 А,
I3 = U / R3= 120/ 60 = 2 А.
По первому закону Кирхгофа, общий ток (в неразветвлённой части цепи) равен сумме токов в ветвях:
Iобщ= I1+ I2 + I3 = 6+4+2 = 12 А.
б) Найдём общее (эквивалентное) сопротивление цепи. Сначала вычислим общее сопротивление для резисторов R1 и R2:
Теперь можно объединить эти два сопротивления в одно и упростить схему. Она примет вид, показанный на рис. 17.
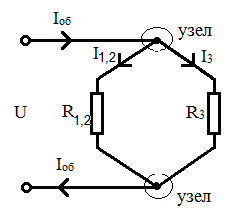
Рис. 17. Вид цепи после объединения резисторов R1 и R2
в одно общее сопротивление R1,2
Вновь использовав формулу для двух резисторов, соединённых параллельно, найдем общее сопротивление всей цепи:
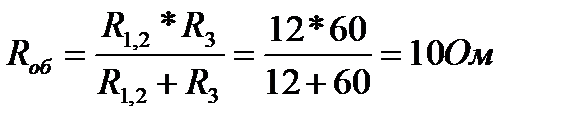
Можно найти общий ток в цепи другим способом, по закону Ома:
I = U/Rобщ = 120/10 =12A
в) Найдём мощность, выделяющуюся в каждой ветви:
P1 = U I1 = 120 •6 = 720 Вт,
P2 = UI2= 120·4 = 480 Вт,
P3 = UI3 = 120·2 = 240 Вт
Мощность всей цепи Робщ = U·Iобщ = 120·12= 1440 Вт.
Можно было найти общую мощность цепи сложив мощности, выделяющиеся в каждом резисторе. Результат будет совпадать с полученным ранее, что подтверждает правильность вычислений.
г) После отключения приемника R1 ток I1станет равен нулю.Токи I2 и I3 останутся прежними, а ток всей цепи уменьшится на величину тока I1 и будет равен:
Iобщ = I1 + I2 + I3 = 0 + 4 + 2= 6 А.
9. Методика расчёта схем со смешанным соединением потребителей.
Смешанное соединение резисторов представляет собой комбинацию последовательного и параллельного соединений. На рис.18а показан пример смешанного соединения. В этой схеме резисторы R2 и R3 соединены параллельно. Последовательно с этими резисторами подключён резистор R1.
При решении задач на смешанное соединение требуется прежде всего, провести анализ схемы. Необходимо нарисовать схему, обозначить все её элементы, а также токи и напряжения, действующие в схеме. Следует мысленно выделить на схеме элементы соединенные параллельно или последовательно и затем, поэтапно, упростить схему.
На рис.18а показана исходная схема, а затем этапы её упрощения на рис.18б и 18в. Заметьте, что номера токов и напряжений, обозначенных на схеме, всегда совпадают с номером соответствующего сопротивления.
Прежде всего, проведено объединение параллельно соединённых резисторов R2и R3в одно сопротивление R2,3. В результате, схема приобрела вид, показанный на рис.18б. На этой схеме видно, что сопротивления R1и R2,3соединены последовательно.
Объединяя сопротивления R1и R2,3, получим общее сопротивление, что показано на рис.18в.
Рис. 18. Смешанное соединение резисторов: а) исходная схема; б) и в) схемы после упрощения
Далее нужно проанализировать схему, рассмотреть, как в ней протекает ток. На схеме, показанной на рис.18а общий для всей схемы ток Iоб, протекая от верхней клеммы, через резистор R1, где он же обозначен как I1, доходит до узла а (см. рис. 18а).
В узле а ток разделяется на две ветви. По первому закону Кирхгофа I1 равен сумме токов I2+I3. Далее эти токи вновь сливаются в общий токIоб, который идёт к нижней клемме. Напряжения на параллельно соединённых резисторах R2и R3 одинаковы.
В схеме на рис. 18б всё уже проще. Видно, что резисторы R1 и R2,3соединены последовательно. Через всю цепь ток, одинаковый во обоих сопротивлениях. Общее напряжение, приложенное к цепи, равно сумме напряжений на резисторахR1 и R2,3.
Совсем просто выглядит схема на рис. 18в. В этой схеме только одно сопротивление.
После упрощения схемы следует записать под каждой из них соотношения для токов и напряжений, используя свойства последовательного и параллельного соединения. Такая запись показана на рис.18. Начинать запись соотношений следует с самой простой схемы, т.е. с рис.18в.
После проведения анализа схемы и её упрощения можно приступать к решению задачи на смешанное соединение? Руководствуясь записанными выше соотношениями для каждой схемы.
Пример 9. Расчёт цепи сосмешанным соединением резисторов
Для схемы, показанной на рис.18 известно общее напряжение, равное 120В
Известна величина каждого сопротивления: R1=16Ом, R2=40Ом и R3=60Ом. Найти: общее сопротивление схемы, все токи и напряжения, обозначенные на схеме.
Решение:
1. Найдём общее сопротивление цепи:
1.1. Общее сопротивление резисторов R2и R3:
1.2. Общее сопротивление всей цепи:
Rоб= R1+R2,3=16+24=40Ом
2. Находим общий ток, потребляемый схемой:
Iоб=Uоб/Rоб=120/40=3А= I1
3. Определяем напряжение на резисторе R1:
U1= I1•R1=3*16=48В
4. Найдём напряжение на параллельно включённых резисторах R2и R3:
U2,3= Uоб - U1 = 120-48=72В =U2=U3
5. Найдем токи в резисторах R2и R3:
I2=U2/R2= 72/40 = 1,8А
I3=U3/R3= 72/60 = 1,2А
