Описание установки
Установка (рис.1) состоит из баллона Б, жидкостного манометра М и набора капилляров (1-5), соединенных с баллоном кранами К1-К5. Давление воздуха в баллоне до необходимого можно повысить с помощью компрессора при открытом кране К и закрытых кранах К1-К5 и К0. Кран К0 используется для быстрого выпускания воздуха из баллона.
Капилляры в установке соединены последовательно. При открытом кране К1 (остальные краны закрыты) воздух вытекает через капилляр 1, имеющий длину ℓ 1. Если открыть только кран К2, то воздух будет вытекать через два последовательно соединенных капилляра 1 и 2, действие которых эквивалентно действию одного капилляра длиной (ℓ 1 + ℓ 2). Если открыть только кран К5, то воздух будет протекать 5 последовательных капилляров с общей длиной (ℓ 1 + ℓ 2 + ℓ 3 + ℓ 4 + ℓ 5).
Примечание: сечение соединительных трубок много больше сечения капилляров и их сопротивлением можно пренебречь.
Методика измерений и расчетные формулы
Вязкость представляет собой пример так называемых явлений переноса. В упрощенной теории вязкости, которая, тем не менее, охватывает все существенные черты данного явления, используются понятия эффективного диаметра и средней длины свободного пробега молекул газа. Молекулы не все время движутся свободно, а время от времени сталкиваются с другими молекулами. В момент столкновения скорость молекулы испытывает резкое изменение как по величине, так и по направлению. В результате траектория молекулы имеет вид ломаной линии с большим количеством звеньев. Для количественного описания явления Клаузиус ввел понятие средней длины свободного пробега < ℓ >, т.е. среднего расстояния, которое пролетает молекула между двумя последовательными столкновениями. Для оценки < ℓ > используется модель твердых шаров, с которыми отождествляются молекулы. Диаметр такого шара называется эффективным диаметром молекулы d и совпадает с минимальным расстоянием, на которое сближаются центры двух молекул. Также предполагается, что движется только одна молекула с постоянной скоростью < υ >– средней тепловой скоростью молекул. Тогда:
, (1)
где k = 1,38·10-23 Дж/К – постоянная Больцмана,
T – абсолютная температура,
m – масса одной молекулы,
R = 8,314 Дж/(моль·К) – универсальная газовая постоянная,
M – молярная масса газа.
Вообразим, что с подвижной молекулой жестко связана концентрическая с ней твердая сфера диаметра 2 d, которую назовем сферой ограждения молекулы. Между двумя последовательными столкновениями подвижной молекулы ее сфера ограждения описывает цилиндр, длина которого и есть длина свободного пробега молекулы. Если центр другой молекулы лежит внутри или на боковой поверхности этого цилиндра, то она столкнется с нашей молекулой, в противном случае столкновения не произойдет. Объем цилиндра, описываемого сферой ограждения в единицу времени, составляет V = πd 2< υ>. Среднее число z столкновений движущейся молекулы с остальными молекулами в единицу времени равно среднему числу последних в объеме V, т.е. z = Vn, где n – число молекул в единице объема, или концентрация. Поэтому z = n π d 2 < υ >. Путь, проходимый молекулой в единицу времени, численно равен скорости молекулы < υ >. Разделив этот путь на среднее число столкновений z, получим среднюю длину свободного пробега < ℓ > = 1/(nπd 2< υ >).
Строгий расчет с учетом максвелловского распределения молекул идеального газа по скоростям дает следующий результат:
, (2)
. (3)
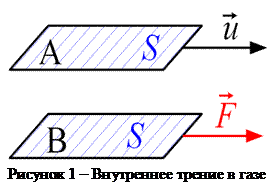Наличие внутреннего трения в газах можно проиллюстрировать на следующем примере: между двумя параллельными пластинками А и B площади S (см. рис. 2) находится воздух или иной газ. При движении пластинки B появляется сила, действующая на пластинку A и направленная в сторону движения. Эта сила и есть сила внутреннего трения. Впрочем, о внутреннем трении можно говорить лишь тогда, когда расстояние между пластинами A и B очень велико по сравнению со средней длиной свободного пробега молекул газа. Тогда от наличия пластин можно отвлечься и говорить о силах, действующих внутри самого газа. Будем представлять себе газ неограниченным и движущимся стационарно плоскопараллельными слоями в горизонтальном направлении. Скорость этого макроскопического движения u меняется в направлении, перпендикулярном к слоям, это направление примем за ось Oy (рис. 2, 3), т.е. предполагается, что u = u (y). Рассечем мысленно газ на две половины плоскостью, параллельной слоям и проходящей через некоторую точку y 0. Допустим для определенности, что скорость u (y) возрастает с увеличением х. Тогда верхняя половина газа будет действовать на нижнюю с силой, направленной вправо, а нижняя на верхнюю – с силой, направленной влево. Это и есть силы внутреннего трения, их величина определяется формулой Ньютона:
, (4)
где η – коэффициент вязкости.
С молекулярной точки зрения происхождение сил внутреннего трения объясняется так: если бы газ покоился, то все направления скоростей его молекул были бы равновероятны, а векторы средней скорости и среднего импульса каждой молекулы были бы равны нулю. При наличии упорядоченного движения газа вектор средней скорости молекулы отличен от нуля и имеет модуль u = u (x). С этой скоростью связан упорядоченный импульс p = mu, которым обладает рассматриваемая молекула. Молекулы, лежащие над плоскостью АВ, обладают более высоким упорядоченным импульсом, чем молекулы, расположенные под ней. Переходя из верхнего полупространства в нижние, молекулы передают часть своего упорядоченного импульса молекулам, с которыми они сталкиваются в нижнем полупространстве. Это проявляется в том, что газ, расположенный ниже плоскости АВ, подвергается действию силы, направленной в сторону скорости u. Аналогично, более медленные молекулы, попадая из нижнего в верхнее полупространство, при столкновениях отнимают часть упорядоченного импульса у молекул, расположенных выше плоскости АВ. В результате газ в верхнем полупространстве испытывает тормозящую силу, направленную против скорости u. Эти силы и являются силами внутреннего трения.
Количественное описание внутреннего трения с помощью рассмотрения потока импульса (который в нашем примере направлен сверху вниз) позволяет получить явное выражение для коэффициента внутреннего трения (вязкости):
, (5)
где ρ = nm – плотность газа.
Для определения коэффициента вязкости воздух продувается через длинный тонкий канал (капилляр) с небольшой скоростью. При малых скоростях потока течение в канале является ламинарным, т.е. поток воздуха движется отдельными слоями, и его скорость в каждой точке направлена вдоль оси канала. Такое течение устанавливается на некотором расстоянии от входа в капилляр, поэтому для достижения достаточной точности эксперимента необходимо выполнение условия r << ℓ к, где r – радиус капилляра, ℓ к – длина капилляра. С другой стороны, радиус капилляра r должен быть достаточно велик по сравнению с < ℓ >, чтобы был задействован механизм внутреннего трения; так, при условиях, близких к нормальным, для «молекул воздуха» эффективный диаметр составляет d ≈ 3,7·10-10 м, длина свободного пробега < ℓ > ~ 6·10-8 м.
В установке воздух предварительно накачивается в баллон компрессором и в процессе измерений выпускается через систему капилляров, соединенных последовательно; давление в баллоне контролируется с помощью жидкостного манометра.
В баллоне создается избыточное над атмосферным P 0 давление Δ P = P – P 0 = ρж gh (ρж – плотность жидкости в манометре, g = 9,81 м/с2 – ускорение свободного падения, h – разность уровней жидкости в коленах манометра). Затем капилляр соединяется с атмосферой, при этом за время dt через капилляр вытекает некоторое количество воздуха объемом dV и массой dm = ρ dV, где ρ – плотность воздуха в капилляре. Давление в капилляре изменяется от P 0 до P 0 + Δ P, но, поскольку Δ P << P 0, то с достаточной точностью можно принять давление воздуха в капилляре равным атмосферному давлению P 0. Тогда плотность воздуха (из уравнения Клапейрона – Менделеева):
. (6)
Объем воздуха dV, прошедшего через капилляр за время dt, описывается формулой Пуазейля:
. (7)
Масса воздуха dm, прошедшего через капилляр за время dt, с учетом (6) составляет:
. (8)
Из уравнения состояния идеального газа выразим изменение массы dm газа в баллоне через уменьшение давления dP в нем:
, (9)
где V б – объем баллона.
Исключая dm из уравнений (8) и (9), получаем:
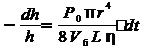. (10)
Решая это дифференциальное уравнение при условии, что за время опыта давление в баллоне уменьшится от ρж gh 0 до ρж gh, получаем рабочую формулу для определения вязкости воздуха:
. (11)
Порядок выполнения работы
Задание 1. Определение коэффициента вязкости воздуха
1) Записать исходные данные:
атмосферное давление: P 0 = _______________________,
радиус капилляра: r = _______________________,
длина капилляра: ℓ 1 = _______________________,
длина 5 капилляров: L = _______________________,
объем баллона: V б = _______________________.
2) При всех закрытых кранах открыть кран К, включить компрессор и накачать в баллон воздух до избыточного давления 140-180 мм водяного столба. Затем компрессор выключить, кран К закрыть.
3) Выждав 1-2 мин., пока не установится постоянное давление в баллоне, открыть кран К5 и одновременно включить секундомер.
4) После того, как давление уменьшится на Δ h = 20 мм водяного столба, снять отсчет времени и остаточную высоту h водяного столба; при этом кран не закрывать и секундомер не выключать. Далее снять отсчеты времени t и высоты h для Δ h = 40, 60, 80 и 100 мм водяного столба. Результаты записывать в таблицу 1.
Таблица 1 – Измерение зависимости остаточного давления в баллоне от времени
| № опыта | h, мм | t, мин:с | t, с | ln(h / h 0) |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
Задание 2. Исследование зависимости расхода воздуха через капилляр от длины капилляра
1) Записать исходные данные:
атмосферное давление: P 0 = _______________________,
радиус капилляра: r = _______________________,
длина капилляра: ℓ 1 = _______________________,
длина 5 капилляров: L = _______________________,
объем баллона: V б = _______________________.
2) При всех закрытых кранах открыть кран К, включить компрессор и накачать в баллон воздух до избыточного давления 100 мм водяного столба. Затем выключить компрессор и закрыть кран К.
3) Открыть кран К1 и включить секундомер.
4) Когда давление в баллоне уменьшится в 2 раза, выключить секундомер и одновременно закрыть кран. Записать длину капилляра и показания секундомера в таблицу 2.
Таблица 2 – Измерение зависимости расхода воздуха от длины капилляра
h 0 = _________________________; h = ________________________.
| № опыта | L, м | t, мин:с | t, с |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
5) Провести аналогичные измерения (пп.2-4) с 2, 3, 4, 5 последовательно соединенными капиллярами; результаты записывать в таблицу 2.
