Темы для предварительной проработки

· Операторы циклаязыка C. Вложенные циклы.

· Условный оператор языка C.

· Матрици.

Задание

Создать квадратную матрицу целых чисел размером 9х9. В индивидуальных заданиях указано, какую обработку матрицы требуется выполнить.

Если по условию задания матрицу следует заполнить случайными числами, рекомендуем выбирать эти числа из диапазона 0 – 99. Если по условию задания в матрицу следует записать ЛП — линейную последовательность чисел, имеется в виду последовательность: 1, 2, 3,... Программу разработатьсиспользованием меню!!!

Варианты индивидуальных заданий

Вариант	Содержание задания	Иллюстрация
1	Заполнить матрицу ЛП, от левого верхнего угла по диагонали: влево — вниз.
2	Заполнить секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями.
3	Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно побочной диагонали
4	Заполнить матрицу случайны­ми числами. Отобразить симметрично относительно вертикальной оси секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей.
5	Заполнить матрицу случайными числами. Отобразить верхнюю половину матрицы на нижнюю зеркально симметрично относи­тельно горизонтальной оси.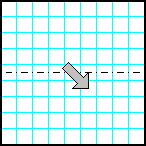
6	Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями.
7	Заполнить матрицу случайны­ми числами. Отобразить главную и побочную диагонали симметрично относительно вертикальной оси.
8	Заполнить матрицу случайны­ми числами. Разместить на главной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к главной.
9	Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей ЛП, от левого верхнего угла вправо — вниз. Остаток матрицы заполнить нулями.
10	Заполнить матрицу случайны­ми числами. Отобразить симметрично относительно горизонтальной оси секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей.
11	Заполнить матрицу случайны­ми числами. Развернуть матрицу на 180o.
12	Заполнить матрицу ЛП, от левого нижнего угла по диагонали: влево — вверх.
13	Заполнить секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей ЛП, от левого верхнего угла вправо — вниз. Остаток матрицы заполнить нулями.
14	Заполнить матрицу ЛП, от левого верхнего угла по диагонали: вправо — вверх.
15	Заполнить матрицу случайны­ми числами. Отобразить главную и побочную диагонали симметрично относительно го­ризонтальной оси.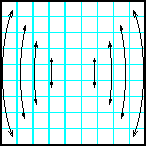
16	Заполнить матрицу ЛП, от правого верхнего угла по диагонали: влево — вниз.
17	Заполнить матрицу случайны­ми числами. Развернуть матрицу на 90o против часовой стрелки.
18	Заполнить матрицу случайны­ми числами. На побочной диагонали разместить суммы элементов, которые лежат на той же строке и столбце.
19	Заполнить матрицу случайны­ми числами. На главной диагонали разместить суммы элементов, которые лежат на той же строке и том же столбце.
20	Заполнить матрицу случайными числами. Отобразить правую половину матрицы на левую зеркально симметрично относи­тельно вертикальной оси.
21	Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от левого верхнего угла по спирали: вниз — вправо — вверх — влево.
22	Заполнить матрицу случайными числами. Отобразить левую половину матрицы на правую зеркально симметрично относи­тельно вертикальной оси.
23	Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от центра по спирали: вниз — влево — вверх — вправо.
24	Заполнить матрицу случайны­ми числами. Развернуть матрицу на 90o по часовой стрелке.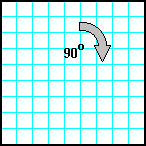
25	Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от центра по спирали: вниз — вправо — вверх — влево.
26	Заполнить матрицу случайны­ми числами. Разбить матрицу на квадраты размером 3х3. В центре каждого квадрата поместить сумму остальных элементов квадрата.
27	Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно глав­ной диагонали
28	Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от левого верхнего угла по спирали: вправо — вниз — влево — вверх.
29	Заполнить матрицу случайными числами. Отобразить нижнюю половину матрицы на верхнюю зеркально симметрично относи­тельно горизонтальной оси.
30	Заполнить матрицу случайны­ми числами. Разместить на побочной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к побочной.
31	Заполнить нечетные диагонали, симметричные побочной, с левого верхнего угла заданнимобразом. Остаток матрицы заполнить нулями.
32	Заполнить главнуюи побочные диагонали матрицы ЛП начинаяс верхнего угла главной диагонали и останавливая заполнение в нижнемуглу побочной диагонали (средин­ную точку заполнявать один раз, если она есть). Остаток матрицы заполнить нулями.
33	Заполнить матрицуиз центра, распространяя ЛП вобестороны параллельно строкам и столбцам.
34	Заполнить матрицу ЛП по диагоналям, симметричным побочной, с левого верхнего угла заданнымобразом — на каждой из диагоналей числа однаковыевдоль нее.
35	Заполнить матрицу ЛП змейкой, начинаяеес левого верхнего угла матрицы вниз изаполняяее на следующем столбце в обратном направле­нии.
36	Заполнить матрицуслучайны­ми числами. Отобразить левые частиглавнойи побочной диагоналей симметрично от­носительно вертикальной оси.
37	Заполнить матрицу ЛП змейкой, начинаяеес нижнего правого угла матрицывлево изаполняяее на следующей строке в обратном направле­нии.
38	Заполнить матрицуиз центра, распространяя ЛП во обе стороны параллельно главной и побочной диагоналям.
39	Заполнить матрицуслучайны­ми числами. На срединных строкахи столбцах разместить суммы элементов, лежащихв соответствующихстрокахи столбцах.
40	Заполнить нечетные диагона­ли, симметричные главной, с правого верхнего угла задан­нымобразом. Остаток матри­цы заполнить нулями.

 

5. Пример решения задачи

Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями.

5.1. Разработка алгоритма решения

Если обозначим размерность матрицы как S, номер строкикак L, а номер столбцакак R, и (имея в виду, что реализация алгоритма будет выполнена на языке С) договоримся, что нумерация строк и столбцов будет начинаться с 0, то можно определить, что в строке с номером L ненулевые элементы в верхней частиматрицы лежат на столбцахс номерами R1=L<R<R2=S–L, а в нижней — R1=S–L–1<R<R2=L. Следовательно, алгоритм может состоять из перебора матрицы строка за строкой с определением для каждого элемента, удовлетворяют ли его индексы вышеприведенным условиям. Если да — элементу присваивается следующее значение из ЛП, если нет — 0.

Но можно несколько упростить алгоритм, обойдя вычисления граничных значений для каждого элемента и необходимости определения, в верхнюю или нижнюю часть матрицы ми попадаем. Обратим внимание на то, что для первой строки (L=0) R1=1, R2=S–2. Для каждой следующей строки R1 увеличивается на 1, а R2 уменьшается на 1..Когда пересекаем середину матрицы, то направление модификации изменяется на противоположное: теперь для каждой следующей строки R1 уменьшается на 1, а R2 увеличивается на 1. Признаком пересечения середины может быть условие R1>R2, оно выполняется в момент пересечения. Схема алгоритма показана на рисунке.

Вместе с описанными выше переменными R1 и R2,, которые получают начальные значения для первой строки матрицы, ми вводим переменную dd сначальным значением 1 — это то значение, которое будет модифицировать R1 и R2 для каждойследующейстроки, ипеременную k — в которой будет значение текущего члена ЛП, начальное значение — 1 (блок 2). Далее организуются вложенные циклы. Во внешнем цикле перебираются строки (блок 3), а во внутреннем — столбцы матрицы (блок 4). В каждой итерации внутреннего цикла номер столбца R сравнивается с граничными значениями R1, R2 (блоки 5,6). Еслион лежит впределахот R1 до R2, то текущему члену матрицы присваивается значенме k — текущего члена ЛП, а потом k увеличивается на 1 (блок 7). Если нет, тотекущему членуприсваивается значения 0 (блок 8).

После выхода из внутреннего цикла модифицируются граничные значения: R1 увеличиваетсяна dd, а R2 уменьшатся на dd (блок 9). Напомним, чтоначальное значение dd =1. Когда выполняется условие R1>R2 (блок 10) присваиваем dd значение –1, далее модификация границ будет соответствовать правилам для нижней части матрицы.

После выхода из внешнего цикла, который начался в блоке 3, вновь организуются вложенные циклы перебора строк (блок 12) и столбцов (блок 13). В каждой итерации внутреннего цикла выводится значение одного элемента матрицы (блок 14), после выхода из внутреннего цикла начинается новая строка вывода (блок 15).