Отношение на множестве. Свойства отношений.

СООТВЕТСТВИЕ.

Понятие о соответствии.

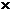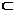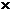Соответствием f между элементами множеств Х и Y называют упорядоченную пару множеств (X Y, G_f), где      G_f  X Y.

Множество Х называют областью отправления, множество Y - обла­стью прибытия, а множество - G_f - графиком этого соответствия.

Из определения следует, что для задания соответствия между эле­ментами множеств Х и Y необходимо указать декартово произведение этих множеств и график G_f, который состоит из пар элементов, нахо­дящихся в этом соответствии.

Областью определения соответствия f =(X 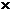Y, G_f)  называется множество тех элементов первого множества (области от­правления), которым соответствуют элементы второго множества (области прибытия).

Множеством значений соответствия f =(X 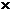Y, G_f)   на­зывается множество элементов из второго множества Y (области при­бытия), которые поставлены в соответствие некоторым элементам первого множества Х (области отправления).

Пусть f - некоторое соответствие между элементами множеств Х и Y. Полным образом элемента а из множества Х называется множество всех элементов у из множества Y, таких, что afy. Полным прообразом элемента b из множества Y называется множество всех элементов х из множества X, таких, что xfb.

Пусть Р - некоторое соответствие между элементами множеств Х и Y. Обратным ему называют соответствие Р^-1 между элементами мно­жеств Y и X, такое, что уР^-1х в том и только в том случае, когда хРу.

 

Соответствие Р¹ между множествами Х и Y называется противопо­ложным соответствию Р, если оно является дополнением соответствия Р до декартова произведения Х 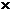Y.

Пример. Отрезки, изображенные на рисунке являются графиком соответствия Р, заданного на множестве действительных чисел. Определите область определения и множество значения данного соответствия.

 

Решение. По чертежу видно, что все абсциссы точек графика соответствия Р принадлежат промежутку [-3,1], а ординаты принад- лежат множеству {1,3}. Множество [-3, 1] есть область определения соотве­тствия Р, а множество {1, 3} - множество значений соответствия Р.

Упражнение 11.

1. Пусть Х - множество столов в аудитории.

            Y - множество студентов.

Через xRy обозначим соответствие "за столом а сидит студент в". Что обозначают множества R(a) и R^-1(b)?  Когда R(a) = Æ?

2. Соответствие R между множествами Х и Y задано при помощи гра­фа. Укажите: а) область отправления, б) область прибытия, в) область определения, г) множество значений, д) график.

3. Даны множества Х ={ 2, 4, 6} и Y ={ 3, 5, 7}. Соответствие R меж­ду множествами X и Y таково: "число х больше числа у". Постройте граф этого соответствия. Постройте графы противоположного и об­ратного соответствия.

4. Дана таблица. Заштрихуйте клетки, стоящие на пересечении таких столбцов А и строк В, что число А кратно В. Что представляет собой множество заштрихованных клеток?

5. Для следующих соответствий сформулируйте противоположные и обратные:

а) точка А лежит на прямой В,

б) число А является корнем уравнения В,

в) число А больше числа В,

г) прямая А пересекает прямую В.

6. Даны два множества А ={-1, -2,-3, 0, 1, 2, 3} и N- множество нату­ральных чисел. Постройте граф соответствия "каждому числу из мно­жества А соответствует его квадрат".

7. Соответствие между множествами А и В задано при помощи графа. Изобразите график соответствия в прямоугольной системе координат. Постройте график обратного и противоположного соответствия.

 

8. Даны множества Х = {xÎZ, -3£х<0}, Y=Z.

Каждому значению х ÎХ поставим в соответствие такое значение у ÎY, которое на 3 больше этого х. Перечислите элементы, принадле­жащие графику соответствия и изобразите его в прямоугольной сис­теме координат. Сформулируйте обратное и противоположное соот­ветствие.

9. Соответствие между множествами С ={1, 2,3,4,5} и             D ={5, 6, 7} таково, что его график состоит из пар, в которых первая компонента взята из множества С, а вторая - из D и больше первой компоненты. Постройте графики этого соответствия и соответствий обратного и противоположного данному.

Виды соответствий.

Соответствие f = (X ×Y, G_f) называется всюду опреде­ленным, если область определения совпадает с первым множеством (областью отправления), т. е. c X.

На графе такого соответствия от каждого элемента первого множества отходит хотя бы одна стрелка.

 

Соответствие f = (X ×Y, G_f) называется сюърективным, если его множество значений совпадает со вторым множеством, т. е. с Y.

На графе такого соответствия к каждому элементу второго множества подходит хотя бы одна стрелка.

 

Соответствие f = (X ×Y, G_f) называется функциональным, если каждому элементу области определения Х соответствует не более одного элемента множества значений Y.

Из этого определения следует, что каждому элементу первого множества либо соответствует только один элемент второго множества, либо не соответствует ни один элемент из второго множества.

Если начертить граф функционального соответствия, то от каждого элемента первого множества, если будет отходить, то только одна стрелка.

Среди всех функциональных соответствий выделяют всюду определенные соответствия. Такие функциональные и всюду определенные соответствия называют отображениями множеств.

 

Соответствие f = (X ×Y, G_f) называется инъективным, если каждый элемент множества Y является образом не более одного элемента из Х.

При инъективном отображении различным элементамиз области определения Х соответствуют различные элементы в области значений Y.

На графе такого соответствия ни к какому элементу второго множества не подходят более одной стрелки (т. е. либо одна, либо ни одной). График такого соответствия не содержит пар с разными первыми и одинаковыми вторыми элементами.

 

Соответствие между элементами множеств X и Y называется взаимно однозначным, если это соответствие является отображением и выполнены следующие два условия:

1) любым двум различным элементам множества Х соответствуют различные элементы множества Y;

2) любой элемент множества Y поставлен в соответствие хотя бы одному элементу из множества Х.

 

Если между множествами А и B можно установить взаимно однозначное соответствие, то такие множества называются равномощными. Обозначается символом A~B. 

 

Пример. Рассмотрим множество Х – пальто и множество Y – номера в гардеробе. Каждому пальто поставим в соответствие номер, на крючке которого оно висит. Это соответствие функциональное (одно пальто не может висеть на двух номерах, но на одном крючке могут висеть два пальто). Может кто-то не сдаст пальто в гардероб, тогда этому пальто не будет соответствовать никакой номер (т. е. это пальто не будет входить в область определения этого функционального соответствия). Множеством значений является множество тех крючков (номеров), на которых висят пальто. Если остались крючки, на которых не висят пальто, то это соответствие не сюръективно.

 

Упражнение 12.

 

1. Х – множество однозначных чисел, Y = {0, 1}. Поставим в соответствие каждому хÎХ его остаток от деления на 2. Является ли это соответствие отображением?

2. Между элементами множеств X и Y задано соответствие «быть делителем». Установите, каков его вид, если:

а) X = {2, 3, 5, 7}, Y{15, 28, 37};

б) X = {2, 3, 5, 7}, Y{15, 21, 30};

в) X = {2, 3, 5, 7}, Y{4, 25, 21}.

3. Какое из заданных соответствий является отображением?

 

4. Можно ли задать отображение следующим образом: множество Х состоит из отрезков, а множество Y из треугольников. Каждому отрезку ставится в соответствие треугольник, для которого этот отрезок является средней линией? Что можно сказать об обратном соответствии?

5. Множество Х состоит из всех квадратов на плоскости, а множество Y – из всех окружностей на той же плоскости. Поставим в соответствие каждому квадрату вписанную в него окружность. Каков вид данного соответствия? Что можно сказать об обратном соответствии?

6. Поставьте между следующими парами множеств знаки «=» или «~».

а) А – множество сторон треугольника, В – множество углов треугольника;

б) А – множество букв в слове «колос», В = {о, к, с, л};

в) А – множество колец на пне дерева, В – множество лет, прожитых данным деревом;

г) А – множество коэффициентов многочлена х³ + 2х² + 3х + 8, В – множество цифр числа 123.

7. Являются ли соответствия, заданные на множестве людей, отображениями, если соответствие задано следующим образом:

а) «человек х сын человека у»,

б) «человек х отец человека у»,

в) «человеку х ставится в соответствие его мать у».

8. Соответствие «фигура х имеет площадь у» задано на множестве М – геометрических фигур. Является ли данное соответствие отображением? Можно ли определить сюръективность или инъективность данного соответствия?

9. Постройте в прямоугольной системе координат графики соответствий, если:

а) х = 2у, -5 £ у £ 5, х, уÎR;

б) х + у £ 4, х ³ 0, у ³ 0, х, уÎR;

в) х = 2, -4 < у < 4, х, уÎR;

г) -3 < х £ 3, -2 £ у < 2, х, уÎR;

д) у = 3, -2 < х < 5, х, уÎR;

е) хÎZ, уÎZ, х = 2, -5 < у < 4;

ж) х + у ³ 6, х ³ 0, у > 0, х, уÎR;

 

 

Отношение на множестве. Свойства отношений.

 

Соответствие, заданное между двумя равными множествами Х=Y, называется бинарным отношением, заданным на множестве Х (или просто отношением).

Для каждого отношения Р между элементами множеств Х и Y существуют отношения, обратное Р и отношение противоположное отношению Р.

 

Отношение Р = (Х, G_P) называется рефлексивным, если любой элемент из множества Х находится в этом отношении с самим собой, т.е. для любого хÎХ имеем хРх.

На графе рефлексивного отношения около каждого элемента будет петля.

 

Отношение Р = (Х, G_P) называется симметричным, если для любых двух элементов х и у из множества Х, для которых выполняется хРу, выполняется и уРх.

На графе симметричного отношения, если от одного элемента к другому идет стрелка, то она двойная.

 

Отношение Р = (Х, G_P) называется транзитивным, если для любых трех элементов х, у и z из множества Х (не обязательно различных) для которых имеет место хРу и уРz, то имеет место и хРz.

На графе транзитивного отношения, если есть стрелка от х к у и от у к z, то должна быть стрелка и от х к z. Однако, это не означает, что любые три элемента должны быть соединены стрелками.

 

Отношение Р = (Х, G_P) называется антирефлексивным, если ни один элемент множества Х не находится в отношении Р с самим собой.

 

Отношение Р = (Х, G_P) называется асимметричным, если ни для каких элементов х и у из множества Х не может случиться, что одновременно хРу и уРх.

 

Отношение Р = (Х, G_P) называется антисимметриным, если хРу и уРх одновременно выполняются в том и только том случае, когда х=у, где х и у элементы множества Х.

 

Отношение Р = (Х, G_P) называется антитранзитивным, если для любых трех элементов х, у, z множества Х из того, что х находится в отношении Р с у и у находится в отношении Р с z следует, что х не находится в отношении Р с z.

 

Отношение Р = (Х, G_P) на множестве Х называется связным, если для любых двух элементов х и у множества Х из того, что х¹у следует, что х находится в отношении Р с у или у находится в Р отношении с х.

 

Упражнение 13.

1. Отношение К: «число х меньше числа у на 2 единицы» задано на множестве А={х│хÎZ, -2£х£2}.

а) перечислите все пары чисел, принадлежащие множеству А, находящиеся в отношении К;

б) сформулируйте отношение обратное и противоположное данному. Постройте их графы и графики.

2. На рисунке сплошными стрелками изображен граф отношения «быть братом», а пунктирным – граф отношения «быть сестрой». Некоторые стрелки пропущены. Восстановите их.

 

 

3. На рисунке изображены графы двух отношений «х отец у» и «х дед у». Какой граф соответствует второму отношению?

 

4. В таблице выделены некоторые отношения, рассматриваемые в начальном курсе математики. Какими свойствами они обладают?

Отношение	равно	меньше	Больше в 2 раза	длиннее	Выше на 3см	Делится нацело
Множество	N	N	N	отрезки	рост	N
Рефлексивно
Симметрично
Транзитивно
Антирефлекс.
Асимметр.
Антисимметр.
Антитранзит.

 

5. Класс выставил на соревнования по плаванию команду мальчиков. В нее входили: Витя, Коля, Андрей и Саша. Коля проплыл дистанцию быстрее Андрея, но медленнее Саши. Андрей затратил на ту же дистанцию времени больше, чем Витя, который плавал медленнее Коли. Как распределились места на соревнованиях?

6. Толя, Володя и Саша живут на одной и той же улице, но в разных домах. На этой же улице находится школа, в которой они учатся. Володя живет от школы не ближе Толи, а Саша – не дальше Толи. Ребята любят приходить в школу вместе. Кто из ребят должен выходить из дома раньше всех, кто – несколько позже и, кто из них встречает двух остальных?

7. Мы наблюдаем за вертолетом, орлом, воздушным шаром и самолетом. Орел находится выше вертолета, вертолет – ниже самолета, но выше воздушного шара, а орел – ниже самолета. В каком порядке расположились по высоте вертолет, орел, воздушный шар и самолет?

8. Известно, что отношение R рефлексивно и транзитивно. Дополните граф этого отношения.