Мережа зв'язку (телекомунікаційна мережа) як об'єкт синтезу й аналізу являє собою сукупність пунктів мережі й сполучуючих їх ліній. За математичну модель такого об'єкта використовують граф.
О з н а ч е н н я. Графом називається деяка сукупність точок і сполучуючих їх стрілок.
Точки графа називаються вершинами, а стрілки – дугами. Граф математично позначається як G(N,V), де N – кінцева множина вершин потужністю n, а V – кінцева множина дуг, потужністю m.
Вершини можна позначити рисими літерами (i, j, k, l, s), або цифрами (1, 2, 3, 4, 5), а дуги відповідно парами: {(i, j), (j, k), (k, l)... } або {(1,2), (2,3), (3,4)... }, де перший індекс означає початок, а другий – кінець дуги.
Рисунок 2.1
Граф, в якому задаєтся напрямок дуг, називається орієнтованим, в противному разі – неорієнтованим. Неорієнтовані дуги називаються ребрами.
Поміж двома вершинами, сполучиними дугою (ребром), існує відношення суміжності (для орієнтованого графа вершини i та j суміжні, лише якщо дуга починається в i й напрямлена в j).
Поміж вершиною і сполученими з нею дугами (ребрами) існує відношення инцидентності.
Граф, кожній дузі (ребру) якого поставлено у відповідність деякі числові характеристики, звані вагами, являє собою зважений граф. За необхідності ваги можуть бути приписані також вершинам графа.
Зважений граф прийнятий називати мережею (в такому разі мається на увазі мережна модель, а не сама мережа як об'єкт). За вагові характеристики мережі можуть виступати відстані, пропускна здатність, вартість тощо.
Крім геометричного зображення у виді точок і ліній граф може бути поданий у дискретній формі. Саме ця форма використовується при введенні графової моделі в ЕОМ.
Одним із найбільше поширених дискретних подань графа є матриця суміжностей. Це матриця А=[aij], розміром (n‘ n) елементів, які можуть набувати значень:
аij = 1, якщо в графі G існує дуга (ребро) поміж вершинами i та j;
аij = 0 – в противному разі.
Матриця суміжностей графа, наведеного на рис.2.1 має вигляд
| A= | 1 1 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 0 1 1 1 1 0 |
Для збереження в пам'яті ЕОМ матриці суміжностей як бачимо, необхідно n2 комірок.
У неорієнтованого графа матриця суміжностей є симетрична щодо головної діагоналі й, отже, в пам'яті ЕОМ може зберігатися лише один з її трикутників, що дозволить заощаджувати пам'ять, але ускладнює обробку цієї матриці на ЕОМ.
Якщо перенумерувати в довільному порядку дуги (ребра) графа G й поставити ці номера у відповідність до номерів рядків деякої матриці В=[bij], а номера стовпчиків залишити, як і раніше, відповідними до номерів вершин графа, то в такій матриці можна відбити відношення і нцидентності елементів графа G. Елементи матриці Bij можуть приймати значення {0,1}.
Перенумеруємо дуги для розглядуваного графа: (i, j) – 1; (j,k) – 2; (k,l) – 3; (l,s) – 4; (s,i) – 5; (s,j) – 6; (s,k) – 7.
Тоді матриця інцидентності матиме вигляд
| B= | 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 1 0 0 1 0 1 |
Зважений граф (мережа) може бути в дискретному виді поданий матрицею вагів W=[wij],де wij – вага дуги (ребра), якщо вона існує в графі G. Ваги неіснуючих дуг (ребер) вважають дорівнюваними "ђ" або "0", в залежності від умов задачі, в якій вони розглядаються.
Якщо граф є розрідженим (має рису кількість дуг (ребер)), те можливе більш компактне поданя графа G – списком дуг (ребер). Цей список може бути зреалізовано двома одновимірними масивами розмірністю m, в першому з яких записано початкові вершини дуг (ребер), а в другому – кінцеві, або двовимірним масивом розмірністю (2,m). Наприклад,
R1 = (1, 3, 4, 5, 5, 2, 5)
R2 = (2, 2, 3, 4, 1, 5, 3)
R =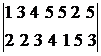 
При організації подання графа у виді дискретного масиву з плаваючими межами, тобто у разі, коли необхідно передбачити можливість додавання чи видалення вершин графа, доцільно використовувати структуру суміжностей. Остання являє собою список суміжних вершин для кожної вершини графа. Структура суміжностей для графа, зображеного на рис. 2.1, має вигляд
1:2 4:3
2:5 5:1, 2, 3, 4.
3:2
