Примечание Дмитрий Гущина.

Задание 1 № 282961

На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 29 литров бензина по цене 24 руб. 30 коп. за литр. Сколько рублей сдачи он должен получить у кассира?

Решение.

Цена бензина составляет 29 24,3 = 704,7 руб. Поэтому причитающаяся сдача составит 295,3 рубля.

Задание 2 № 501593

На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 23 ноября по 23 декабря 2012 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа курс евро был наименьший за указанный период.

Решение.

Из диаграммы видно, что курс евро был наименьшим восьмого числа (см. рисунок).

Ответ: 8.

Задание 3 № 27846

На клетчатой бумаге с размером клетки 1 1 изображён параллелограмм. Найдите длину его большей высоты.

Решение.

Проведем высоту DH из вершины D. По рисунку находим ее длину.

Ответ: 4.

Задание 4 № 285926

В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по теме "Ботаника". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Ботаника".

Решение.

Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна

Ответ: 0,2.

Задание 5 № 504406

Найдите корень уравнения

Решение.

Последовательно получаем:

Ответ: −0,5.

Задание 6 № 27888

Найдите величину угла Ответ дайте в градусах.

Решение.

Центральный угол, опирающийся на хорду АС равен 90°, поэтому меньшая дуга окружности, отсекаемая этой хордой, также равна 90°, а большая — равна 270°. Опирающийся на нее вписанный угол ABC равен ее половине т. е. 135°.

Ответ: 135.

Задание 7 № 509990

На рисунке изображен график — производной функции определенной на интервале (−3; 19). Найдите количество точек максимума функции принадлежащих отрезку [−2; 15].

Решение.

Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−2; 15] функция имеет одну точку максимума x = 10.

Ответ: 1.

Задание 8 № 27161

Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

Решение.

Исходный и отсеченный конус подобны с коэффициентом подобия 2. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площадь отсеченного конуса в 4 раза меньше площади поверхности исходного. Тем самым, она равна 3.

Ответ: 3.

Задание 9 № 500953

Найдите значение выражения

Решение.

Имеем:

Ответ:6.

Задание 10 № 513901

Груз массой 0,05 кг колеблется на пружине. Его скорость v меняется по закону где t — время с момента начала колебаний, T = 12 с — период колебаний, м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 11 секунд после начала колебаний. Ответ дайте в джоулях.

Решение.

Найдем скорость груза через 11 секунд после начала колебаний:

Найдем кинетическую энергию груза через 11 секунд после начала колебаний:

Ответ: 0,009

Задание 11 № 510489

Из одной точки кольцевой дороги, длина которой равна 12 км, одновременно в одном направлении выехали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение.

Пусть скорость второго автомобиля равна км/ч. За 1/3 часа первый автомобиль прошел на 12 км больше, чем второй, отсюда имеем

Ответ: 65.

Задание 12 № 77492

Найдите точку максимума функции , принадлежащую промежутку

Решение.

Найдем производную заданной функции:

На заданном промежутке (первая четверть без граничных точек) синус не обращается в нуль и принимает только положительные значения. Поэтому единственный нуль производной — число 1,5.

Определим знаки производной функции: она положительна при x < 1,5 и отрицательна при x > 1,5. Поэтому искомая точка максимума — число 1,5.

Ответ: 1,5.

Задание 13 № 507665

Решите уравнение

Решение.

Левая часть уравнения имеет смысл при Выражение положительно при всех допустимых Значит,

Учитывая, что и получаем, что решениями являются числа

Ответ:

Задание 14 № 513347

Все рёбра правильной четырёхугольной пирамиды SABCD с вершиной S равны 6. Основание высоты SO этой пирамиды является серединой отрезка SS ₁, M — середина ребра AS, точка L лежит на ребре BC так, что BL: LC = 1: 2.

а) Докажите, что сечение пирамиды SABCD плоскостью S ₁ LM — равнобокая трапеция.

б) Вычислите длину средней линии этой трапеции.

Решение.

Прямая S ₁ M пересекает медиану AO треугольника ABD в точке T так, что АТ: TO = 2: 1, поскольку T — точка пересечения медиан треугольника SAS ₁ и O — точка пересечения диагоналей основания ABCD, так как пирамида SABCD правильная.

Следовательно, AT: TC = 1: 2. Точка L делит отрезок BC в отношении BL: LC = 1: 2, следовательно, треугольники ACB и TCL подобны с коэффициентом подобия k = AC: TC = BC: CL = 3: 2, так как они имеют общий угол с вершиной C и стороны AC и BC в треугольнике ABC пропорциональны сторонам TC и LC треугольника TCL, заключающим тот же угол. Значит, сторона сечения, проходящая через точки L и T, параллельна стороне AB основания пирамиды SABCD. Пусть эта сторона сечения пересекает сторону AD в точке P.

Сторона сечения, проходящая через точку M в плоскости SAB, параллельна прямой AB, так как плоскость S ₁ LM пересекает плоскость SAB и проходит через прямую PL, параллельную плоскости SAB. Пусть эта сторона сечения пересекает сторону SB в точке K. Тогда сечение PMKL — равнобокая трапеция, поскольку AP = BL и AM = BK.

Большее основание LP трапеции равно 6, поскольку ABCD — квадрат. Второе основание MK трапеции равно 3, поскольку MK — средняя линия треугольника SAB. Значит, средняя линия трапеции равна

Ответ: б) 4,5.

Задание 15 № 484584

Решите неравенство

Решение.

Разделим обе части неравенства на

Решение будем искать при условиях

При этих условиях получаем неравенство:

Таким образом, множество решений исходного неравенства:

Ответ:

Задание 16 № 514605

В прямоугольном треугольнике АВС с прямым углом С точки М и N — середины катетов АС и ВС соответственно, СН — высота.

а) Докажите, что прямые МН и NH перпендикулярны.

б) Пусть Р — точка пересечения прямых АС и NH, а Q — точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

Решение.

а) Треугольники АНС и ВНС прямоугольные (рис. 1), поэтому и Значит, треугольники MCN и MHN равны по трём сторонам, откуда

б) В прямоугольном треугольнике АВС имеем: (рис. 2).

В прямоугольном треугольнике МНР и MCQ с общим углом CMH получаем:

поэтому треугольники МНС и MРQ подобны с коэффициентом подобия

Площадь S треугольника МНС равна половине площади треугольника АНС, то есть

Найдём

Значит, площадь треугольника MPQ равна

Ответ: б) 50.

Примечание Дмитрий Гущина.

Площадь треугольника PQM равна половине произведения QC на PM. Для того, чтобы определить длины данных отрезков, можно два раза применить теорему Менелая:

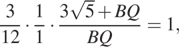
откуда:

Задание 17 № 517449

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

− каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.

Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.

Решение.

Пусть сумма кредита S ежегодные выплаты x, По условию долг на июль меняется так:

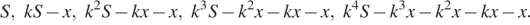
Если долг выплачен двумя равными платежами x ₂, то откуда

Если долг выплачен четырьмя равными платежами x ₄, то откуда

Тогда

откуда Следовательно,

Ответ: 10.

Задание 18 № 484649

Найдите все положительные значения при каждом из которых система имеет единственное решение.

Решение.

Если то уравнение задает окружность с центром в точке радиуса а если то оно задаёт окружность с центром в точке того же радиуса (см. рис.).

При положительных значениях параметра уравнение задаст окружность с центром в точке 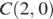радиуса Поэтому задача состоит в том, чтобы найти все значения параметра при каждом из которых окружность имеет единственную общую точку с объединением окружностей и

Из точки проведём луч и обозначим и точки его пересечения с окружностью где лежит между и

Так как 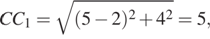то

При или окружности и не пересекаются. При окружности и имеют две общие точки. При или окружности и касаются.

Из точки проведём луч и обозначим и 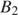точки его пересечения с окружностью где лежит между точками и Так как 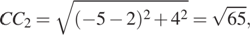то

При или окружности и не пересекаются. При окружности и имеют две общие точки. При или окружности и касаются.

Исходная система имеет единственное решение тогда и только тогда, когда окружность касается ровно одной из двух окружностей и и не пересекается с другой. Так как то условию задачи удовлетворяют только числа и

Ответ:

Задание 19 № 520827

а) Представьте число в виде суммы нескольких дробей, все числители которых — единица, а знаменатели — попарно различные натуральные числа.

б) Представьте число в виде суммы нескольких дробей, все числители которых — единица, а знаменатели — попарно различные натуральные числа.

в) Найдите все возможные пары натуральных чисел m и n, для которых и .

Решение.

а) Приведем пример такой суммы: .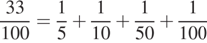

б) Приведем пример такой суммы: .

в) Пусть m = dp, n = dq, где d — наибольший общий делитель чисел m и n. Тогда . Числа p, q и p + q попарно взаимно простые, поэтому числа p и q являются взаимно простыми делителями числа 14. Получаем следующие варианты:

p	q	d	m	n
1	1	28	28	28
1	2	21	21	42
1	7	16	16	112
1	14	15	15	210
2	7	9	18	63

Ответ:

а) Да, например, ;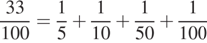

б) Да, например, ;

в) 28 и 28, 21 и 42, 16 и 112, 15 и 210, 18 и 63.