1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии.
Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего 
оценить ее математическое ожидание а. Будем рассматривать выборочное среднее 
как случайную величину 
а значения вариант выборки х 1, х 2,…, хп как одинаково распределенные независимые случайные величины Х 1, Х 2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М (
) = а, 
(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства 
. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
р (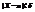
) = 2Ф 
. Тогда, с учетом того, что , р () = 2Ф 
=
=2Ф(t), где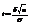 
. Отсюда 
, и предыдущее равенство можно переписать так:
.
Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал 
, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии.
Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания построим новую случайную величину
, (18.2)
где 
- выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента (см. лекцию 12) с k = n – 1 степенями свободы.
Поскольку плотность распределения Стьюдента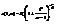 
, где 
, явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ, tγ), учитывая четность плотности распределения, следующим образом: 
. Отсюда получаем: 
(18.3)
Таким образом, получен доверительный интервал для а, где tγ можно найти по соответствую-щей таблице при заданных п и γ.
26. Элементы теории корреляции. Выборочное уравнение регрессии. Линейная регрессия. Пусть составляющие Х и Y двумерной случайной величины (Х, Y) зависимы. Будем считать, что одну из них можно приближенно представить как линейную функцию другой, например Y ≈ g (Х) = α + β Х, (11.2) и определим параметры α и β с помощью метода наименьших квадратов. Определение 11.2. Функция g (Х) = α + β Х называется наилучшим приближением Y в смысле метода наименьших квадратов, если математическое ожидание М (Y - g (Х))2 принимает наименьшее возможное значение; функцию g (Х) называют среднеквадратической регрессией Y на Х. Теорема 11.1. Линейная средняя квадратическая регрессия Y на Х имеет вид: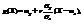 
(11.3)где 
- коэффициент корреляции Х и Y. Доказательство. Рассмотрим функцию F (α, β) = M (Y – α – βX)² (11.4) и преобразуем ее, учитывая соот-ношения M (X – mx) = M (Y – my) = 0, M ((X – mx)(Y – my)) = = Kxy = r σ x σ y: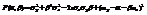 
. Найдем стационарные точки полученной функции, решив систему 
Решением системы будет 
. Можно проверить, что при этих значениях функция F (α, β) имеет минимум, что доказывает утверждение теоремы. Определение 11.3. Коэффициент 
называется коэффициентом регрессии Y на Х, а прямая 
- (11.5) - прямой среднеквадратической регрессии Y на Х.
Подставив координаты стационарной точки в равенство (11.4), можно найти минимальное значение функции F (α, β), равное 
Эта величина называется остаточной дисперсией Y относительно Х и характеризует величину ошибки, допускаемой при замене Y на g (Х) = α + β Х. При 
остаточная дисперсия равна 0, то есть равенство (11.2) является не приближенным, а точным. Следовательно, при 
Y и Х связаны линейной функциональной зависимостью. Аналогично можно получить прямую среднеквадратической регрессии Х на Y: 
(11.6) и остаточную дисперсию Х относительно Y. При 
обе прямые регрессии совпадают. Решив систему из уравнений (11.5) и (11.6), можно найти точку пересечения прямых регрессии – точку с координатами (тх, ту), называемую центром совместного распределения величин Х и Y. Линейная корреляция. Для двумерной случайной величины (Х, Y) можно ввести так называемое условное математи-ческое ожидание Y при Х = х. Для дискретной случайной величины оно определяется как 
(11.7) для непрерывной случайной величины – 
. (11.8) Определение 11.4. Функцией регрессии Y на Х называется условное математическое ожидание M (Y / x) = f (x). Аналогично определяется условное математическое ожидание Х и функция регрессии Х на Y. Определение 11.5. Если обе функции регрессии Х на Y и Y на Х линейны, то говорят, что Х и Y связаны линейной корреляционной зависимостью. При этом графики линейных функций регрессии являются прямыми линиями, причем можно доказать, что эти линии совпадают с прямыми среднеквадратической регрессии. Теорема. Если двумерная случайная величина (Х, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью. Доказательство. Найдем условный закон распределения Y при Х = х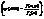 
, используя формулу двумерной плотности вероятности нормального распределения (11.1) и формулу плотности вероятности Х: 
. (11.9) Сделаем замену 
. Тогда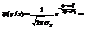 
= 
.
Полученное распределение является нормальным, а его мате-матическое ожидание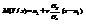 
есть функция регрессии Y на Х (см. опреде-ление 11.4)). Аналогично можно получить функцию регрессии Х на Y: 
. Обе функции регрессии линейны, поэтому корреляция между Х и Y линейна, что и требовалось доказать. При этом уравнения прямых регрессии имеют вид 
, 
, то есть совпадают с уравнениями прямых среднеквадратической регрессии (см. формулы (11.5), (11.6)).
