2.1 Формула Лагранжа, интерполяционный многочлен:
Теорема 4.1:
Для любых х0<х1< х2…<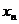 
и у0, у1, у2… 
существует единственный многочлен рÎ 
(т.е. многочлен р в степени £ n) такой, что р(xi) =уi, i = 
Доказательство:
Докажем сначала единственность многочлена р. Предположим, что существует два интерполирующих многочлена р1 и р2. Имеем P1(xi)=yi
P2(xi) = 
, где 
. Рассмотрим многочлен h=P1-P2, очевидно его степень не выше n, с другой стороны он имеет как минимум (n+1) корней. Как известно из алгебры, у ненулевого многочлена степени n имеет не более n корней, а наш многочлен h имеет (n+1) корней, следовательно он тождественно равен 0. h≡0 и P1=P2 Докажем теперь существование многочлена р: рассмотрим для этого следующий набор многочленов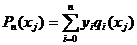 
(4.2а)
где 
(4.2b)
Заметим, что все qi многочлены степени n, следовательно, Pn(x) будет многочлен степени не выше n. Докажем, что pn(x) искомый, т.е. pn(xi)=yi для этого подсчитаем qi в точках xi
(*)
Так как один из сомножителей в числителе занулится. Учитывая (*) приходим к выводу
, т.е. для данного многочлена (4.2) выполняется свойство интерполяции. Осталось заметить, что степень многочлена из формулы (4.2) не выше n.
Частные случаи интерполяционного многочлена Лагранжа:
n=1 (интерполируем по двум точкам)
n=2 (интерполируем по трем точкам)
n=3 (интерполируем по четырем точкам)
Замечание:
Интерполяционный многочлен из формулы (4.2) называют интерполяционным многочленом Лагранжа. Вообще говоря, интерполяционный многочлен единственен, как доказано в теореме 4.1, но вариантов для вычисления этого многочлена (формул) существует много. Все они выдадут в одной точке один и тот же результат, но вариантов для вычисления будет много. Каждый из этих вариантов (формул интерполяционного многочлена) имеет свои достоинства и недостатки.
Рассмотрим следующий вариант вычисления интерполяционного многочлена.
2.2 Схема Эйткена:
Теорема 3.2:
если (1) 
- многочлен, интерполирующий функцию f в точках x0..xn-1 (степени не выше n-1), а (2) 
- многочлен, интерполирующий функцию в точках x1…xn (степени не выше n-1), то многочлен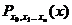 
- многочлен, интерполирующий функцию в точках x0…xn (степени не выше n) может быть вычислена по формуле:
(4.3)
Доказательство:
Заметим, что многочлен 
имеет степень не выше n, так как каждый из многочленов (1) и (2) имел степень не больше чем (n-1), мы домножали на многочлен первой степени.
Осталось проверить, что данный многочлен в узлах интерполяции задает значения yi. 
Рассмотрим три возможности:
1. Проверим, что свойства интерполяции выполняются и в крайних точках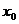 
и :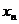
а) 
б) 
2. Проверим, что (4.3)-интерполирующий, если i – не крайние точки:
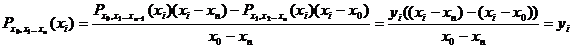
Замечание:
В теореме 4.2 приведем другой способ вычисления интерполяционного многочлена, существование и единственность которого были доказаны в теореме 4.1. В теореме 4.1 была формула Лагранжа, в теореме 4.2 схема Эйткена.
Обобщим формулу из теоремы 4.2:
(4.4)
На основании (4.4) и очевидного наблюдения 
(т.к. мы должны подобрать многочлен 0-ой степени значение которого в т. 
), приходим к следующей картине для вычисления интерполяционного многочлена:
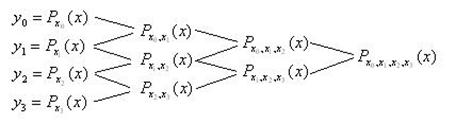
(4.5)
(4.5) – схема Эйткена вычисления интерполяционного многочлена, все слияния производятся по формуле (4.4).
Оценим трудоёмкость вычисления интерполяционного многочлена по формуле Лагранжа и по схеме Эйткена:
1) Формула Лагранжа:
(n+1) слагаемых, в каждом 2n умножений +1 деление + 2n (+/-). Итого 
2) Схема Эйткена:
Слияний на первом этапе – (n-1), на втором (n-2), …, итого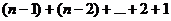 
В каждом действии 4(+/-) + 2(*) + 1(/) таким образом, 
действий.
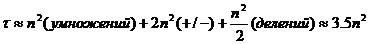
С одной стороны в формуле Лагранжа количество операций немного больше, но в схеме Эйткена на порядок больше деления.
1. Главное достоинство схемы Эйткена состоит в том, что вычисления по этой схеме можно оборвать в любой момент, при этом мы получим многочлен, который интерполирует функцию не во всех точках, а лишь в некоторых, но его значение будет близко к И.М. В формуле Лагранжа прерывать вычисления раньше времени нельзя.
2. Схема Эйткена более устойчива к вычислительным погрешностям.
Поэтому можно прибавлять по одному узлу интерполяции слева и справа, пока не достигнем заданной точности (универсальный критерий прерывания).
2.3 Погрешности интерполяционного многочлена:
При интерполировании возникает два типа погрешностей:
1. погрешность усечения (возникает из-за замены функции на интерполирующий многочлен);
2. погрешность округления (возникает из-за того, что значения интерполируемой функции f в узлах интерполяции известны не точно, а приближенно, с некоторой погрешностью η)
Обычно возникает из-за того, что значения функции в точках Xi – округляются.
Замечание: если мы округляем до 4-х знаков, то погрешность 
.
Теорема 4.3 (оценка 
при интерполировании многочлена):
εусеч с учетом знака для интерполирующего многочлена (остаточный член И.М.) 
может быть вычислен по формуле 
где 
- точное значение, 
- приблизительное значение, 
- (n+1) производная, С некоторая точка 
- наименьший интервал, который содержит все узлы интерполяции.
Функция f должна быть (n+1) раз непрерывно дифференцируема.
Доказательство:
Рассмотрим П(x)=(x-x0)…(x-xn) со старшим коэффициентом равным 1.
Введем функцию U(x)=rn(x)-kП(x), где k некоторая const подобранная специальным образом, для этого фиксируем точку 
, не совпадающую ни с одним узлом интерполяции
, то есть подбираем k так, чтобы 
Следовательно, функция U на интервале [x0,xn,x] обращается в 0, как минимум (n+2) раза. Тогда, ее производная U΄ обращается в 0, как минимум (n+1) раз. U΄΄ как минимум n раз. Следовательно, U(n+1) обращается на этом интервале хотя бы один раз в 0, т.е. существует 
 |
- т.к. этот многочлен степени (n+1) 0 т.к. (n+1) производная равна 0
Заменим 
на x и получим формулу.
Следствие 4.4:
(4.7)
Замечание:
(4.7) – удобна тем, что в ней нет т.С – местоположение которой мы не знаем.
Пример:
Вычисление интерполяционного многочлена и оценка εусеч в узлах
x0=100, x1=121, x2=144, y0=10, y1=11, y2=12.
Найдем 
, используя интерполяцию по трем точкам.
εреальное=1٠10-3
Оценим εусеч: 
εокр=0, т.к. значения функции в узлах интерполяции были известны точно.
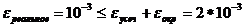
Замечание:
Заметим, что с увеличением числа узлов интерполяции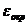 
быстро стремится к 
, а
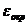
Необходимо, чтобы были бы малы. Для этого число узлов интерполяции должно быть не слишком маленьким (т.к. будет велико), но и не слишком большим (т.к. 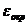будет велико).
Если же узлов много, то возьмем ближайшие значения, а остальные откинем.
2. 4. Конечные разности.
Формулы Ньютона интерполяционного многочлена.
Конечной разностью функции у=f(х) называется функция 
, где h – фиксированный шаг. Конечные разности иногда называются конечными разностями первого порядка.
Функция обозначается: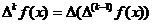 
Принимаем 
Считаем:
Таблица конечных разностей:
Если функция f(x) задана своими значениями yi в равноотстоящих узлах xi с шагом h, xi=x0+ih, 
, то конечные разности в точках xi удобно вычислять с помощью таблицы конечных разностей.
Рассмотрим функцию f(x)=2x3-2x2+3x-1
xi=x0+ih=0+i*1, 
| x | y | Δy | Δ2y | Δ3y | Δ4y | Δ5y |
| 0 | -1 | 3 | 8 | 12 | 0 | 0 |
| 1 | 2 | 11 | 20 | 12 | 0 | |
| 2 | 13 | 31 | 32 | 12 | ||
| 3 | 44 | 63 | 44 | |||
| 4 | 107 | 107 | ||||
| 5 | 214 |
Наблюдения:
1. Каждый раз длина столбца уменьшается на 1, при n=5 доходим до 
.
2. Конечная разность похожа на производную, в нашем случае – многочлен третей степени, поэтому 
не нулевые (следующие - нулевые)
Теорема 4.4 (о связи между конечной разностью и производной):
Если функция f, n – раз непрерывно дифференцируема, то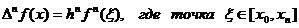 
Комментарии:
При n=1 это в чистом виде теорема Лагранжа из курса мат.анализа.
Удобно записывать формулу интерполяционного многочлена через конечные разности (1-ую и 2-ую формулы Ньютона интерполяционного многочлена)
Первая формула Ньютона ИМ:
(4.9) 
где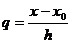 
Вторая формула Ньютона ИМ:
(4.10) 
y – убывает, т.к. столбец уменьшается.
Комментарии:
1. В 1-ой формуле Ньютона 
берем из нулевой строки таблицы конечных разностей.
2. Во 2-ой формуле Ньютона берем из нижней побочной диагонали в таблице конечных разностей.
3. И 1-ая и 2-ая формулы Ньютона могут быть оборваны, если мы возьмем в 1-ой формуле Ньютона не (n+1) слагаемых, а (k+1) (до 
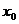), то мы получим интерполяционный многочлен, который интерполирует функцию в (k+1) крайних точках (от до 
).
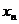Аналогичным образом и со 2-ой формулой Ньютона (т.е. возьмем не (n+1) слагаемых, а (k+1) (до ), то мы получим интерполяционный многочлен, который интерполирует функцию в (k+1) крайних точках (от до 
)).
4. И в том и в другом случае мы можем оборвать вычисления раньше времени, используя универсальный критерий прерывания.
5. При добавлении 1-го нового слагаемого, в 1-ой формуле Ньютона мы добавляем один новый узел интерполяции, двигаясь слева направо, а во 2-ой формуле Ньютона – справа налево.
Погрешности формул Ньютона ИМ:
Т.к. формула Ньютона один из вариантов вычисления ИМ, то формулы для и 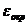можем взять прежние.
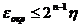
По теореме 4.3:
по теореме 4.4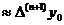 
(4.11)
Комментарии:
Как мы видим из формулы (4.11) в формуле Ньютона есть ничто иное как первое отбрасываемое слагаемое. Таким образом, при вычислении по формуле Ньютона, мы постоянно оцениваем и в нужный момент мы можем прервать вычисления.
