Установившиеся режимы в электрической системе описываются законами Ома и Кирхгофа или вытекающими из них уравнениями узловых напряжений и контурных токов.
Запишем основные матрицы, используемые при расчетах режимов в электрической системе. Будем помнить, что комплексные величины обозначаются точкой сверху.
- Вектор-столбец токов в ветвях графа сети 2. Вектор-столбец узловых токов
3. Матрица сопротивлений ветвей графа является диагональной матрицей, если недиагональные элементы равны нулю при отсутствии взаимоиндуктивности между ветвями. Диагональные элементы равны сопротивлениям соответствующих ветвей.
| ветви | |||
| Z b = | в е т в и | 
|
где  - комплексное сопротивление i -й ветви
|
Произведение матрицы сопротивлений ветвей Z b на матрицу токов в ветвях 
позволяет получить матрицу падений напряжения в сопротивлениях ветвей 
| Z b ∙ Ib = | 
| 
| 
| 
|
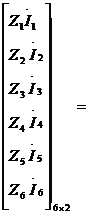
или в общем виде
- закон Ома в матричной форме при отсутствии ЭДС в ветвях.
Умножим первую матрицу инциденций М на вектор-столбец 
ветвей графа сети
| МIb = |   
|
| 
| 
|
Первый элемент матрицы произведения есть не что иное как алгебраическая сумма токов, проходящих к первому узлу. Эта сумма равна узловому току, т.е. 
. То же самое справедливо для остальных элементов матрицы произведения. Следовательно, можно записать
- первый закон Кирхгофа в матричной форме.
Умножим вторую матрицу инциденций N на матрицу падений напряжений в ветвях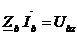 
.
|
N= | I |
|
|
|
| II |
Первый элемент матрицы есть не что иное, как сумма падений напряжений при обходе по ветвям первого контура. Мы знаем, что эта сумма при отсутствии ЭДС в ветвях равна 0, т.е.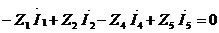 
- второй закон Кирхгофа для первого контура.
Следовательно, второй закон Кирхгофа в матричной форме
или 
.
Прямой ” расчет токораспределения в электрической сети
Заключается в том, что составляется система линейных уравнений по первому и второму законам Кирхгофа и решается известным Вам методом:
число уравнений (R – 1) + (n – R + 1) = n
Расчет называется “прямым”, потому что токи вычисляются без каких-либо предварительных преобразований уравнений первого и второго законов Кирхгофа. “Прямой” способ обычно не применяется, так как не очень сложные предварительные преобразования позволяют получить эквивалентную систему уравнений с меньшим числом уравнений и более однородных по виду, что облегчает численное решение системы. Это достигается при использовании методов узловых напряжений и контурных токов. Отметим, что, как правило, при расчетах время преимущественно расходуется на решение систем уравнений.
