Создание имитационной модели абстрактного автомата Тьюринга средствами ExcelMSOffice. Создание имитационной модели нормального алгоритма Маркова (НАМ).

Поиск: Рекомендуем:  Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки) Нейроглия (или проще глия, глиальные клетки)
Категории:
|
Выполним задачу по работе нормального алгоритма Маркова (НАМ).
Создание имитационной модели абстрактного автомата Тьюринга средствами ExcelMSOffice. Создание имитационной модели нормального алгоритма Маркова (НАМ).
| ||
| Выполнил: студент группы Б02-071-1зт Братухин А.А. Проверил: шамсиахметов о.я. | |||
| Ижевск 2018 | |||
Лабораторная работа №1.1
Цель работы: Понять принцип работы машины Тьюринга
Ход работы:
Краткая теория.
Структура машины Тьюринга Машина Тьюринга (МТ) состоит из двух частей - ленты и автомата (рис. 1):

Рис 1. Машина Тьюринга.
Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые не имеют нумерацию и имена. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться - в неё можно записать другой символ или стереть находящийся там символ.
Автомат - это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ - видимый символ; содержимое соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний q1, q2 и т.п. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы b на a), находясь в другом состоянии - другую операцию.
1) Выполним задачу по автомату Тьюринга:
A={a,b}. В непустом слове Р поменять местами его первый и последний символы.

Рис. 2 Задачу по автомату Тьюринга
2) Составляем текстовый алгоритм выполнения задачи по шагам:
1. Начальное положение программы “0” →вводим исходные данные на ленту и определяем положение головки цифрой “1” в клетке под записанными данными на ленте.
2. Запускаем программу →положение программы “1”.
3. Оцениваем содержимое ячейки ленты над головкой и состояние головки.
4. По результатам оценки находим в таблице автомата Тьюринга данные о новом состоянии, новом движении головки и новом содержимом ячейки над головкой.
5. Сдвигаем головку в нужном направлении, одновременно изменяя ее состояние. При этом записываем нужную информацию в ячейку ленты.
6. Если состоянии головки равно наибольшей строке таблицы+1, то изменяем положение программы на “2” и останавливаем программу выполнения.
Остается уточнить детали алгоритма и составить формулы для нужных ячеек электронной таблицы.
Составим подробный текстовый алгоритм по минимальным шагам выполнения программы:
1. Начальное положение программы “0” →вводим исходные данные на ленту (строка 16) и определяем положение головки цифрой “1” (Ручной ввод информации, строка 17).
2. Запускаем программу →положение программы “1”.(добавляем в определенную ячейку “1” вместо “0”)
3. Оцениваем содержимое ячейки ленты над головкой, состояние головки и находим в таблице автомата Тьюринга данные о новом состоянии головки, новом движении головки и новом содержимом ячейки числа (“a” или “b” или пустота (обозначим ее “х”) над головкой (добавляем три новых ячейки информации для каждого положения головки, помимо ячеек информации ленты) (это Шаг 1)
4. Сдвигаем головку в нужном направлении, одновременно изменяя ее состояние. (это Шаг 2).
5. Переписываем содержимое новой ячейки числа в ячейку ленты там, где была головка.
6. Обнуляем ячейки состояния головки и состояния движения. Ячейки состояния числа сохраняем(там остаточная информация (ее не обнуляем)).
7. Далее повторяем пункты 3÷6 пока состояние головки не станет максимальным (равным наибольшей строке таблицы автомата Тьюринга +1).
8. Если состоянии головки равно наибольшей строке таблицы+1, то изменяем положение программы на “2” и останавливаемся.
1. Головка находится в середине слова, в 1-ом состоянии и записывает в ячейку тоже символ.
2. Головка сдвигается на одну ячейку вправо.
3. Головка остается в 1-ом состоянии.
4. Если ячейка не пуста, то головка записывает в нее тот же символ.
5. Головка сдвигается на одну ячейку вправо.
6. Головка остается в 1-ом состоянии.
7. Если ячейка пуста, головка оставляет ее пустой, сдвигается влево.
8. Головка переходит во 2-ое состояние.
9. Головка меняет символ.
10. Сдвигается влево.
11. Меняет свое состояние на третье.
12. Записывает в ячейку тот же символ.
13. Сдвигается влево.
14. Остается в 3-ем состоянии.
15. Если ячейка пуста, головка оставляет ее пустой, сдвигается вправо.
16. Меняет свое состояние на 4-ое.
17. Меняет символ в ячейке.
18. Меняет свое состояние на 5-ое.
19. Конец.
3) Опишем управляющие формулы.
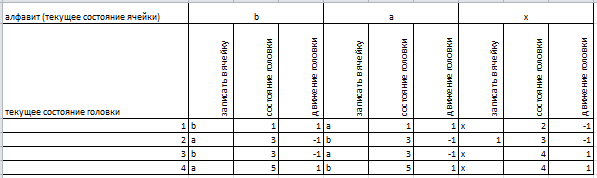
Рис. 3 Таблица автомата Тьюринга для всех элементов алфавита и всех состояний головки
1. Таблица автомата Тьюринга для всех элементов алфавита и всех состояний головки (кроме состояния останова программы - обычно его не пишут ввиду повторяемости ячеек с одинаковым содержимым). (ячейки A1-J5(по диагонали)) управляющие формулы не нужны (мы будем ссылаться на эту таблицу) (Рис 3).
2. Ячейка Пуск (ячейка B11) →управляющие формулы не нужны.
3. Ячейка Шаг (ячейка B13)→.
=ЕСЛИ(D11=2;"конец";ЕСЛИ(D11;ЕСЛИ(C11=1;СУММ(B13;1);B13);"начало"))

| Рис. 4 Блок-схема ячейки B13 |
4. Изображение ленты с заданным на ней числом→ указываем вручную заданное число в любом месте ленты (ячейки B16-AH16).
5. Изображение начального положения головки (обязательно над числом в любом месте) цифрой 1-указываем вручную. (ячейки B17-AH17)
6. Изображение действующей ленты с ячейками состояния (для ячейки B20)
=ЕСЛИ($D$11=2;B20;ЕСЛИ($D$11;ЕСЛИ($C$11=4;;ЕСЛИ($C$11=1;ЕСЛИ(B24;ВПР(B24;$A$3:$J$6;ПОИСКПОЗ(B23;$A$1:$J$1;)+1;);B20);B20));))

| Рис. 5 Блок схема ячейки B20 |
Необходимо заполнить подобными формулами ячейки B 20- AH 20 с учетом их относительных адресов.
У адресов ячеек где проставлен знак $ при протаскивании адреса не изменяться.
7. Изображение действующей ленты с ячейками движения(для ячейки B21)
=ЕСЛИ($D$11=2;B21;ЕСЛИ($D$11;ЕСЛИ($C$11=4;;ЕСЛИ($C$11=1;ЕСЛИ(B24;ВПР(B24;$A$3:$J$6;ПОИСКПОЗ(B23;$A$1:$J$1;)+2;);B21);B21));))
h AIWoWKzFAAAA2wAAAA8AAABkcnMvZG93bnJldi54bWxEj0FrwkAQhe8F/8MygjfdVKHR6CpWKRR7 UVvE45idJqHZ2ZBdNf33nYPQ2wzvzXvfLFadq9WN2lB5NvA8SkAR595WXBj4+nwbTkGFiGyx9kwG finAatl7WmBm/Z0PdDvGQkkIhwwNlDE2mdYhL8lhGPmGWLRv3zqMsraFti3eJdzVepwkL9phxdJQ YkObkvKf49UZmKWTk0/Pk2673lcfs9frLs0vO2MG/W49BxWpi//mx/W7FXyBlV9kAL38AwAA//8D AFBLAQItABQABgAIAAAAIQAEqzleAAEAAOYBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9U eXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhAAjDGKTUAAAAkwEAAAsAAAAAAAAAAAAAAAAAMQEAAF9y ZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABIAAAAAAAAAAAAAAAAALgIAAGRy cy9waWN0dXJleG1sLnhtbFBLAQItABQABgAIAAAAIQCFqFisxQAAANsAAAAPAAAAAAAAAAAAAAAA AJ8CAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABAD3AAAAkQMAAAAA "> 
| Рис. 6 Блок схема ячейки B21 |
Необходимо заполнить подобными формулами ячейки B 21- AH 21 с учетом их относительных адресов.
8. Изображение действующей ленты с ячейками числа (для ячейки B22)

| Рис. 7.Блок схема ячейки B22B22 |
Блок-схема действия формулы представлена на рисунке 7.
Необходимо заполнить подобными формулами ячейки B 22- AH 22 с учетом их относительных адресов.
9. Изображение действующей ленты с ячейками текущего числа ленты (для ячейки B23)
=ЕСЛИ($D$11=2;B23;ЕСЛИ($D$11;ЕСЛИ($C$11=3;B22;B23);B22))

| Рис.8 Блок схема ячейки B23 |
Необходимо заполнить подобными формулами ячейки B 23- AH 23 с учетом их относительных адресов.
10.Ячейки номера состояния головки (для ячейки B24)
=ЕСЛИ($D$11=2;B24;ЕСЛИ($D$11=1;ЕСЛИ($C$11=2;ЕСЛИ(A21=1;A20;ЕСЛИ(C21=-1;C20;));B24);B17))
Блок-схема действия формулы представлена на рисунке 9:

| Рис.9 Блок схема ячейки B24 |
Необходимо заполнить подобными формулами ячейки B 24- AH 24 с учетом их относительных адресов.
11. Ячейка для промежуточной информации о положении программы (ячейка D11) =ЕСЛИ(B11;ЕСЛИ(МАКС(B24:AH24)=МАКС($A$3:$A$7)+1;2;B11);)
Блок-схема действия формулы представлена на рисунке 10:
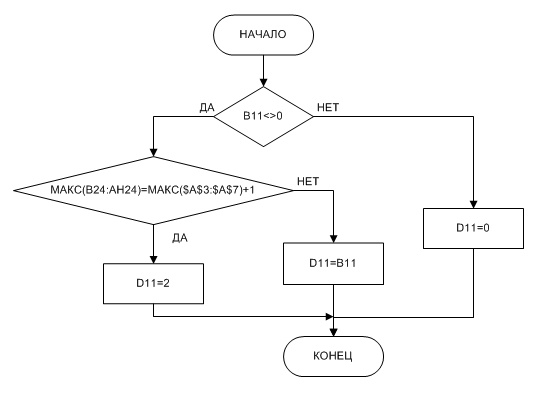
| Рис.10 Блок схема ячейки D11 |
12. Ячейка для промежуточной информации о шаге выполнения (ячейка С11) =ЕСЛИ(D11;ЕСЛИ(C11=4;1;C11+1);1)
Блок-схема действия формулы представлена на рисунке 11:

Рис.11 Блок схема ячейки C11
Вывод: Таким образом мы сымитировали алгоритм работы модели Тьюринга и поняли его принцип действия, что находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы b на a), находясь в другом состоянии - другую операцию.
Лабораторная работа №1.2
Цель работы: Понять принцип работы нормального алгоритма Маркова (НАМ).
Ход работы:
Краткая теория
Особенностью нормальных алгоритмов Маркова (НАМ) является использование одного элементарного действия - подстановки, которая определяется следующим образом.
Формулой подстановки называется запись вида α→β (читается «α заменить на β»), где α и β - любые слова включая пустые. При этом α называется левой частью формулы, а β - правой частью.
Сама подстановка (как действие) задается формулой подстановки и применяется к некоторому слову Р. Суть операции сводится к тому, что в слове Р отыскивается часть, совпадающая с левой частью этой формулы (т.е. с α), и она заменяется на правую часть формулы (т.е. на β). При этом остальные части слова Р (слева и справа от α) не меняются. Получившееся слово R называют результатом подстановки. Условно это можно изобразить так:
P xαy → R xβy
Если левая часть формулы подстановки входит в слово Р, то говорят, что эта формула применима к Р. Но если α не входит в Р, то формула считается неприменимой к Р, и подстановка не выполняется.
Если левая часть α входит в Р несколько раз, то на правую часть β, по определению, заменяется только первое вхождение а в Р:
P xαyαz → R xβyαz
Если правая часть формулы подстановки - пустое слово, то подстановка а→ сводится к вычеркиванию части α из Р (в формулах подстановки не принято как-либо обозначать пустое слово):
P xαy →R xy
Если в левой части формулы подстановки указано пустое слово, то подстановка →β сводится, по определению, к приписыванию в слева к слову Р:
P x →R βx
Формула с пустой левой частью применима к любому слову. Формула с пустыми левой и правой частями не меняет слово.
Нормальным алгоритмом Маркова (НАМ) называется непустой конечный упорядоченный набор формул подстановки:
α1→β1
α2→β2
(k≥1)
αk→βk
В этих формулах могут использоваться два вида стрелок: обычная стрелка и стрелка «с хвостиком» (!→). Формула с обычной стрелкой называется обычной формулой, а формула со стрелкой «с хвостиком» - заключительной формулой.
Записать алгоритм в виде НАМ - значит предъявить набор формул.
Выполним задачу по работе нормального алгоритма Маркова (НАМ).
Используя программу Excel составить машину Маркова
Дан алфавит А={ d, f }. Требуется приписать символ “ d ” к концу слова Р.
Пример: ffdf →ffdfd
Решение:
Заданное словоffdf, в столбце «старт» - 0
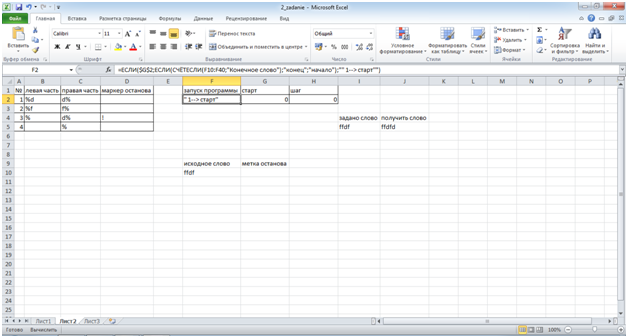
Рис.12 Машина Маркова в Excel
Заданное слово ffdf→ffdfd, в столбце «старт» - 1.

Рис.13 Машина Маркова в Excel
Составим подробный текстовый алгоритм по минимальным шагам выполнения программы:
Ячейка F2(информационная(начало,конец))-содержимое =ЕСЛИ($G$2;ЕСЛИ(СЧЁТЕСЛИ(F10:F40;"Конечное слово");"конец";"начало");"'' 1→старт''")
Блок-схема действия формулы представлена на рисунке 14:

| Рис.14 Блок схема ячейки F2 |
Ячейка H2-содержимое =ЕСЛИ(G2;ЕСЛИ(H2=100;1;H2+1);0)
Блок-схема действия формулы представлена на рисунке 15:

| Рис.15 Блок схема ячейки H2. |
Ячейка F2-(информационная (начало,конец))
Первое правило→Условное форматирование→ Использовать формулу для форматируемых ячеек →
=$ F $2=”начало”
и выбрать цвет и шрифт (цвет желтый и шрифт по умолчанию),
в графе Применяется к добавить
F $2
Второе правило→Условноеформатирование→Использовать формулу для форматируемых ячеек →набрать формулу =$ F $2=”конец”
и выбрать цвет и шрифт (у нас цвет красный и шрифт по умолчанию), а также в графе Применяется к добавить
F $2
3. Создаем таблицу исходной задачи.
Создается таблица на любом пустом месте листа Excel в виде двух столбиков (Задано слово и Получить слово).
В единственной строке указываем данные задачи (у нас ffdf и ffdfd).
4. Оформляем таблицу решений.
Ячейка F9-содержимое “Исходное слово”
Ячейка G9-содержимое “Метка останова”
Ячейка F10-содержимое “ffdf”
Ячейка G10-содержимое “0”
Ячейка F11-

| Рис.16 Блок схема ячейки F11. |
Содержимое F11
=ЕСЛИ($ H $2>=СЧЁТЗ($ F $11: F 11);ЕСЛИ(G 10=1;"Конечное слово";ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $2; F 10;1));ЗАМЕНИТЬ(F 10;ПОИСК($ B $2; F 10;1);ДЛСТР($ B $2);$ C $2);ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $3; F 10;1));ЗАМЕНИТЬ(F 10;ПОИСК($ B $3; F 10;1);ДЛСТР($ B $3);$ C $3);ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $4; F 10;1));ЗАМЕНИТЬ(F 10;ПОИСК($ B $4; F 10;1);ДЛСТР($ B $4);$ C $4);ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $5; F 10;1));ЗАМЕНИТЬ(F 10;ПОИСК($ B $5; F 10;1);ДЛСТР($ B $5);$ C $5);"стоп")))));"")
Необходимо повторить с некоторыми изменениями содержание этой ячейки в ячейках F12-F18 (воспользоваться приемом Excel “протаскивание”).
Необходимо помнить, что адреса ячеек со знаками $ не меняются от протаскивания.
Ячейка G11(метка останова на шаге)-содержимое
=ЕСЛИ(F 11="Конечное слово";1;ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $2; F 10;1));ЕСЛИ(И(ЕЧИСЛО(ПОИСК($ B $2; F 10;1));ЕТЕКСТ($ D $2));1;0);ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $3; F 10;1));ЕСЛИ(И(ЕЧИСЛО(ПОИСК($ B $3; F 10;1));ЕТЕКСТ($ D $3));1;0);ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $4; F 10;1));ЕСЛИ(И(ЕЧИСЛО(ПОИСК($ B $4; F 10;1));ЕТЕКСТ($ D $4));1;0);ЕСЛИ(ЕЧИСЛО(ПОИСК($ B $5; F 10;1));ЕСЛИ(И(ЕЧИСЛО(ПОИСК($ B $5; F 10;1));ЕТЕКСТ($ D $5));1;0);0)))))

| Рис.17 Блок схема ячейки G11. |
Заполняем ячейки методом протаскивания для G11÷G18.
Ячейка E11(шаг с номером)-содержимое
=ЕСЛИ($H$2>=1;"шаг " & ЕСЛИ(ЕПУСТО(F11);"";СЧЁТЗ($F$11:F11));"")
Блок-схема действия формулы представлена на рисунке 18

| Рис.18 Блок схема ячейки E11. |
Вывод: Таким образом мы сымитировали алгоритм нормального алгоритма Маркова (НАМ) и поняли его принцип работы,что в слове Р отыскивается часть, совпадающая с левой частью этой формулы (т.е. с α), и она заменяется на правую часть формулы (т.е. на β). При этом остальные части слова Р (слева и справа от α) не меняются. Получившееся слово R называют результатом подстановки
|
|
|
|
|
Дата добавления: 2018-11-11; Мы поможем в написании ваших работ!; просмотров: 1444 | Нарушение авторских прав
Лучшие изречения: