Лабораторная работа № 1.
ПОЛНЫЙ И ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ
1. Цель и задачи работы: изучение методов реализации и обработки результатов полного и дробного факторных экспериментов.
Общие положения (теоретические сведения)
В полном (ПФЭ) и дробном (ДФЭ) экспериментах каждый из факторов варьируется на двух уровнях. Поэтому всегда можно провести нормализацию факторов так, чтобы рассматриваемым уровням каждого фактора соответствовали значения +1 (верхний уровень) и –1 (нижний уровень).
Полный факторный эксперимент (далее ПФЭ) 2 n
Модель, которую можно построить, используя ПФЭ, включает в себя все линейные факторы и все эффекты взаимодействия. Так, для 3-х факторов можно построить модель вида:
,
где 
, 
– эффекты взаимодействия.
Число точек спектра плана ПФЭ 
. Геометрически точки плана ПФЭ 
размещаются в вершинах гиперкуба.
План называется насыщенным, если число точек плана равно числу оцениваемых параметров модели. По отношению к модели, учитывающей все эффекты взаимодействия, ПФЭ представляет собой насыщенный план.
Для рассматриваемого примера плана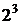 
матрица 
имеет вид таблицы:
| № п/п |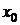 
| 
| 
| 
| 
| 
| 
| 
|
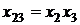
| 1 2 3 4 5 6 7 8 | + + + + + + + + | + – + – + – + – | + + – – + + – – | + + + + – – – – | + – – + + – – + | + + – – – – + + | + – + – – + – + | + – – + – + + – |
Матрица 
ПФЭ обладает свойствами:
1. 
при 
, 
;
2. 
при 
, 
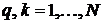– свойство ортогональности;
3. 
, .
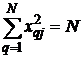Информационная матрица Фишера 
для ПФЭ является диагональной:
, обратная 
Решение системы нормальных уравнений методом наименьших квадратов дает вектор коэффициентов
.
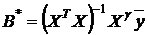Для ПФЭ коэффициенты можно рассчитывать по упрощенной формуле:
, 
. (1)
Реализация плана завершается обработкой экспериментальных данных, в которую включается:
1. Проверка воспроизводимости эксперимента.
2. Оценка дисперсии шума.
3. Вычисление оценок коэффициентов модели.
4. Определение дисперсии оценок коэффициентов модели.
5. Проверка значимости коэффициентов модели.
6. Проверка адекватности модели.
Проверка воспроизводимости представляет собой проверку предпосылки регрессионного анализа о постоянстве дисперсии шума:
.
Считается, что это условие выполнено, если справедлива гипотеза о равенстве построчных дисперсий матрицы плана
.
Для проверки этой гипотезы в каждой строке спектра плана проводятся 
параллельных опытов:
, 
, 
.
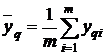Проверка проводится с помощью критерия Кохрена. Статистика критерия Кохрена имеет вид:
.
Если 
, где 
, то считается, что экспериментальные данные на уровне значимости 
не противоречат гипотезе о равенстве дисперсий (обычно 
).
Для вычисления 
можно воспользоваться таблицей статистики Кохрена или воспользовавшись таблицами F -распределения 
с помощью соотношения:
Оценка дисперсии шума вычисляется по формуле
.
Число степеней свободы 
. Коэффициенты модели рассчитываются по формуле (1). Дисперсия оценок коэффициентов 
рассчитывается:
, 
.
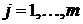В случае отсутствия параллельных опытов дисперсия равна:
.
Проверка значимости коэффициентов – это проверка значимости отличия их шумовой компоненты.
Статистика для проверки этой гипотезы:
.
Если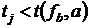 
, то гипотеза о незначимости 
принимается.
Если 
, то коэффициенты значимы.
Здесь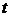 
– квантиль распределения Стьюдента с числом степеней свободы 
и уровнем значимости .
Незначимые коэффициенты исключаются из модели без пересчета остальных.
Причины незначимости:
1) переменная не влияет на отклик 
;
2) действие переменной не проявляется на фоне помехи; в этом случае надо увеличить физический интервал варьирования данным параметром;
3) центр плана находится в районе частного экстремума по данному фактору.
Проверка адекватности модели основывается на оценке отклонения предсказанного модельного отклика 
от результата 
.
Рассчитывается дисперсия адекватности:
,
где 
– число значимых коэффициентов, включая 
.
Проверка адекватности производится по F-критерию Фишера.
Если
,
где 
; 
, то можно считать, что модель адекватна при заданном уровне .
Если модель неадекватна, то необходимо либо уменьшить интервал варьирования факторов, либо усложнить модель.
Адекватность модель можно оценить и другим способом.
Рассчитывается постоянная составляющая 
, равная среднему значению в центре плана:
.
Оценивается значимое различие 
с помощью критерия Стьюдента:
.
Если 
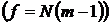, то разница между и значима и полученная модель неадекватна.
Дробный факторный эксперимент (далее - ДФЭ) 2 n - p
Реальные объекты, как правило, могут быть описаны с помощью моделей с меньшим числом составляющих, чем при ПФЭ.
Задача ДФЭ состоит в сокращении числа опытов, с сохранением при этом оптимальных свойств матрицы X, т.е. Мы уменьшаем число строк матрицы спектра плана таким образом, чтобы для нового спектра плана, как минимум, выполнялись оптимальные свойства, которым обладал ПФЭ 2n.
Так, построение матрицы дробного факторного эксперимента на примере ПФЭ типа 
, производится приравниваем произведения 
к третьей независимой переменной 
.
| № п/п |
|
|
|
|
| 1 2 3 4 | + + + + | – + – + | – – + + | + – – + |
Реализация такого плана позволяет вычислить , 
, 
, 
.
При ДФЭ происходит смешивание теоретических коэффициентов модели. Каждый коэффициент рассматриваемой модели является оценкой двух теоретических коэффициентов:
;
;
;
.
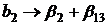Коэффициенты, входящие в сумму правой части, не могут быть оценены раздельно. ДФЭ, представляющий половину плана ПФЭ типа , носит название "полуреплики" от ПФЭ типа , или плана 
. Смешивание необходимо проводить таким образом, чтобы основные коэффициенты 
смешивались при коэффициентах при взаимодействиях, которые на основании априорных сведений не оказывают влияния на объект.
При большом числе переменных для получения линейного приближения строятся дробной реплике 
, 
переменных приравнены к произведениям переменных. ДФЭ строится путем приравнивания переменных к различным произведениям. При этом меняется система совместных оценок теоретических коэффициентов.
В ДФЭ существуют два специальных термина: генерирующее соотношение и определяющий контраст.
Так для полуреплики генерирующими соотношениями могут служить
и 
.
Выражение определяющего контраста получается умножением левой и правой частей приведенного генерирующего соотношения на заменяемую переменную. Так, для полуреплики определяющий контраст имеет вид 
, так как всегда 
.
Определяющий контраст помогает найти всю систему совместных оценок ДФЭ. Для планов высокой степени дробности строится обобщенный определяющий контраст на основе перемножения между собой всех частных, определяющих контрастов. Так, для плана 
при выборе генерирующих соотношений 
, 
частные определяющие контрасты будут иметь вид:
, 
;
а обобщенный определяющий контраст в нашем случае равен
.
Совместные оценки будут определяться вспомогательными соотношениями:
;
;
.
Аналогично можно получить соотношения для 
, 
, 
и т.п.
Эти соотношения позволяют установить. Оценками каких теоретических коэффициентов являются коэффициенты регрессии:
;
;
;
.
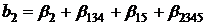Аналогично можно найти оценки смешивани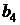я 
, 
, 
, 
. В этом примере все линейные коэффициенты смешаны с коэффициентами при парных взаимодействиях, поэтому разрешающая способность плана невысокая.
Следует отметить, что проведение эксперимента, проверка воспроизводимости, получение математической модели при ДФЭ и проверка ее адекватности совпадают с аналогичными процедурами ПФЭ.
