Тема 4. Тригонометрические ряды Фурье
Периодические функции и их свойства
В науке и технике часто приходится иметь дело с периодическими процессами: колебательными движениями деталей машин, приборов, движением небесных тел и элементарных частиц, электромагнитными колебаниями и т.д. Математически такие процессы описываются периодическими функциями.
Функция f (x), определенная на всей числовой оси, кроме, может быть, некоторых точек, называется периодической с периодом Т, если существует такое число Т≠0, что для любого значения х из области определения функции выполняется равенство:
f (x + T) = f (x).
Если число Т является периодом функции f (x), то число Т·п при любом целом п так же будет периодом этой функции.
Наименьший из положительных периодов данной функции называют основным периодом функции.
Например, любую константу можно рассматривать как периодическую функцию с каким угодно периодом. Наиболее известными периодическими функциями с периодом Т = 2π являются тригонометрические функции у = sin х, у = cos х..
Свойства периодических функций
1. Сумма, разность, произведение и частное периодических функций с периодом Т есть периодическая функция с тем же периодом.
2. Если функция f (x) имеет период Т, то функция f (a · x) имеет период 
, где а ≠0, а = const.
Например, так как функции y = sin x, y = cos x являются периодическими с периодом Т=2π, то функции y = sin kx и y = cos kx также являются периодическими и имеют период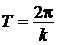 
. Функции y = sin kx и у = cos kx называют «простыни гармониками».
3. Определенный интеграл от периодической функции по отрезку, который равен периоду, не зависит от положения отрезка интегрирования на оси, т.е. если f (x) = f (x + T), тo 
.
Геометрически для неотрицательных функций это свойство означаетравенство площадей закрашенных областей фигур (рисунок 2).
Рисунок 2
Ортогональные системы функций
Рассмотрим несколько вспомогательных понятий, которые потребуются нам в дальнейшем.
Функции f (x) и φ(х) называются ортогональными на отрезке [ а, b ], если они определены, интегрируемы на этом отрезке и выполняется равенство
.
Например, рассмотрим функции f (x)= х и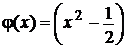 
на отрезке [0, l]. Они определены и непрерывны на отрезке [0;1]. Найдем определенный интеграл от произведения этих функций по указанному отрезку:
.
Следовательно, функции f (x) = x и 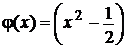ортогональны на отрезке [0,l].
Система функций f,(x), f 2 (x),…, fn (x) называется ортогональной на отрезке [ a, b ], если любые две различные функции ортогональны, т.е.
В качестве примера приведем систему {1, cos x, sin x, cos2 x, sin2 x,..., cos nx, sin nx,... }, п ÎZ,которая является ортогональной системой функций на отрезке [-π, π], т.е. является ортогональной системой на отрезке, равном периоду этих функций.
