Построение минимального остовного дерева

Методы и модели теории графов

Элементы теории графов

Рис. 1. Несвязный неориентированный граф

Для неориентированного графа на рис. 2 множество вершин X и ребер U можно записать так:

X = (х₁, …х₇)

U = ((х₁,х₁),(х₁,х₂)…(х₄, х₅), (х₅, х₆))

Рис. 2 Ориентированный граф

Для ориентированного графа множества вершин и дуг записываются следующим образом:

X = (х₁, …х₇)

U = ((х₁,х₂),(х₁,х₃), (х₃, х₂), (х₃, х₃), (х₃, х₄))

Рис. Графы

Самостоятельно. Для гамильтонова графа указать гамильтонову цепь и гамильтонов цикл.

Матрицей смежности графа, содержащего n-вершин, называется квадратная матрица А (n*m), каждый элемент которой определяется следующим образом:

- 1, если вершины i и j соединены ребром или дугой;

- 0, в противном случае.

Матрицей инцидентности ориентированного графа с n вершинами и m ребрами называется матрица В с n строками и m столбцами, элемент которой определяется следующим образом:

1, если вершина является началом ребра (i, j);

-1, если вершина является концом ребра (i, j);

2, если вершина и начало, и конец ребра (i, j);

0, если вершина и ребро не инцидентны.

Самостоятельно. Для неориентированного графа (рис. 1) построить матрицу смежности. Для ориентированного графа (рис. 2) построить матрицу смежности и инцидентности.

2. Природа потоков в сетях и принцип их сохранения

Рассматривается сеть с одним узлом входа (источник) и одним узлом выхода (сток). Какова максимальная величина потока (количество машин, сообщений, и т.д.), который может войти в сетевую систему и выйти из нее в заданный период времени?

Условное изображение в сети

означает, что мощность потока от узла 1 к узлу 2 равна 6, а мощность потока от узла 2 к узлу 1 равна 0, то есть это — «улица с односторонним движением».

Условное же изображение

означает, что мощность потока в каждом направлении равна 2.

Алгоритм определения максимального потока:

Полагаем искомую величину максимального потока равной нулю.

Шаг 1. Найти какой-нибудь путь от источника до стока, который образован дугами, каждая из которых имеет в направлении потока ненулевую мощность. Если такого пути нет, то оптимальное решение найдено.

Шаг 2. Найти наименьшее значение мощности дуги P на выбранном пути шага 1. Увеличить поток через сеть на эту величину.

Шаг 3.. На пути из шага 1 сократить на P мощности потоков на всех дугах в направлении потока и увеличить на эту же величину мощности потоков на всех дугах в обратном направлении. Перейти к шагу 1

Пример. Система автодорог «Север — Юг», проходящих через Псковскую область, может обеспечить пропускные способности, показанные на приводимой ниже схеме (тыс. автомашин в час).

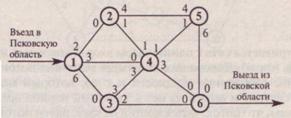
1. Каков максимальный поток через эту систему (тыс. автомашин в час)?

2. Сколько автомашин должно проехать по дороге 5—6, чтобы обеспечить максимальный поток?

Решение.

Самостоятельно.

Чему равен максимальный поток автомашин для системы автодорог? Рассматривается возможность введения секции 3—4 с пропускной способностью 3 тыс. автомашин в час. На сколько увеличится величина максимального потока автомашин?

Построение минимального остовного дерева

Определение. Остовным деревом сети называется дерево, содержащее все узлы сети.

Сеть с пятью узлами:

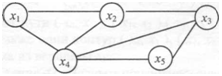Построить остовные деревья.

Алгоритм построения минимального остовного дерева сети

1. Выбрать произвольный узел сети х_i, C₁ = ‹x_i›, C₁¹ = X\‹x_i›

2. Выбрать из оставшихся узлов узел x_j, ближайший к множеству узлов C₁:

C₂ = ‹x_i, x_j›, C₂¹= X\‹x_i, x_j›

3. Выбрать из множества С₂¹, узел, ближайший к узлам множества С₂, включить его в множество С₂ и исключить из множества С₂¹.

4. Т.д. За конечное число шагов будут обработаны все узлы сети и построено минимальное остовное дерево.

Пример. Компания планирует подключение к кабельной сети пяти новых районов. Структура планируемой сети и расстояния между пунктами заданы рисунком.

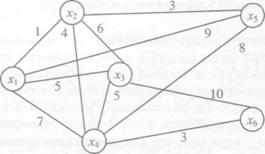
Требуется спланировать наиболее экономичный маршрут. Необходимо провести пошаговое построение минимального остовного дерева для данной сети.

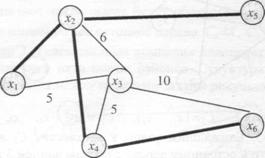
Самостоятельно.

1. Для сетей, изображенных на рисунке, найдите по три остовных дерева.

2. Компания проектирует строительство складских помещений в некоторых пунктах области. Структура сети и расстояние между населенными пунктами приведены на схеме. Необходимо рассмотреть возможность построения транспортной сети минимальной протяженности, охватывающей все пункты.

3. В модульных перевозках трейлерные платформы перевозятся по железной дороге между перевалочными железнодорожными терминалами. На схеме показаны железнодорожные терминалы и пути между ними. Выделите сегменты железных дорог так, чтобы были связаны все железнодорожные терминалы.

4. На рисунке показаны расстояния между платформами, добывающими газ в открытом море, и приемным пунктом, расположенным берегу. Платформа х1 оснащена оборудованием для перекачки газа остальных платформ к приемному пункту. Требуется спроектировать сеть трубопроводов минимальной длины.

4. Предположим, что в условиях предыдущей задачи все платформ разбиты на две группы в зависимости от давления газа в скважинах к группе с высоким давлением относятся платформы х1, х2, х4, х6, с низких давлением — х5, x7, x8 и х9. Из-за разницы давлений газопроводы разнь групп нельзя соединить между собой. Газопроводы от этих групп могут подсоединяться к приемному пункту через платформу х1. Требуется спроектировать сеть трубопроводов минимальной длины в данной ситуации.