Исходные данные к задаче 1

Вариант	№ схемы	Р Кн.
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	10

Рис. 1

Вариант

	Схема	а, м	F, кН	м, кнм	q, кН/м
1	1
2	2
3	3
4	4
5	5
6	6	1	8	22	3
7	7
8	8
9	9
10	10

Задача 2 «а»: определить реакции в опорах для балки. Данные для задачи своего варианта взять из таблицы 2 и схемы на рисунке 2 «а»;

Задача 2 «б»: определить реакции в опорах для рамы. Данные для задачи своего варианта взять из таблицы 2 и схемы на рисунке 2 «б».

 

 

Таблица 2

 

Исходные данные к задаче 2 «а», 2 «б»

 

Рис. 2 «а»

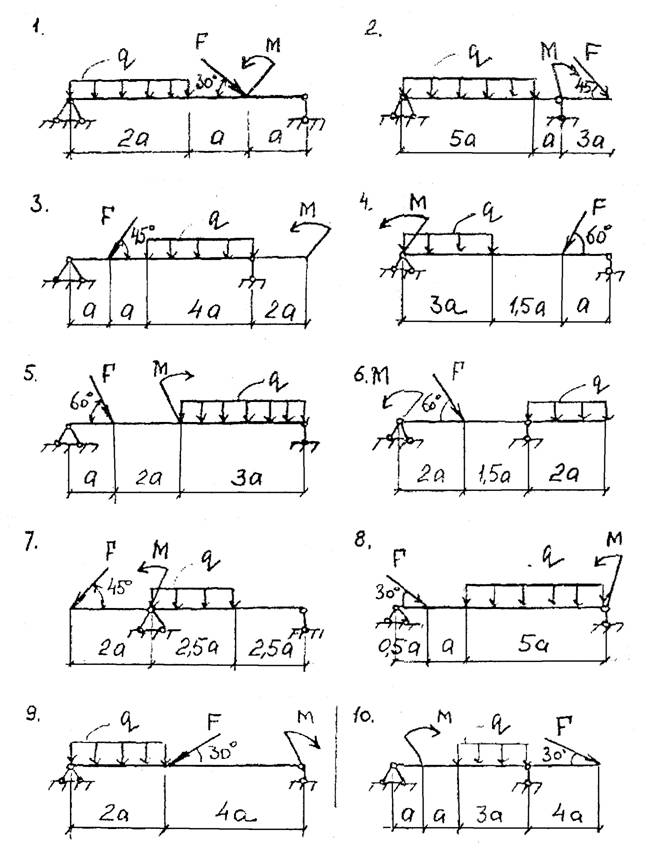
Рис. 2 «б»

 

Задача 3 Определить главные центральные моменты инерции сечения, составленного из прокатных профилей. Данные для задачи своего варианта взять из таблицы 3, схема на рисунке 3

 

Таблица 3

Исходные данные к задаче 3

Вариант	Схема	№ профиля	лист
			b x h, мм
1	1	10	92	4
2	2	10	80	4
3	3	10	100	4
4	4	10	-	-
5	5	10	-	-
6	6	8	80	4
7	7	10	100	4
8	8	10	100	4
9	9	12	-	-
10	10	12	-	-

 

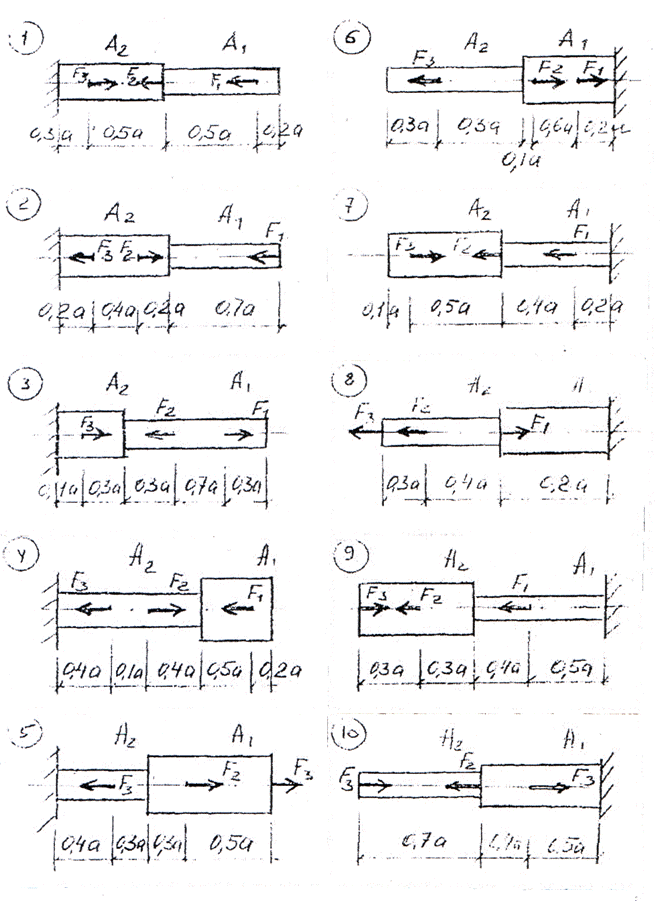
Задача 4 Двухступенчатый стальной брус нагружен силами F₁; F₂; F_3. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆1 свободного края бруса, если Е = 2 х 10⁵ Н/мм². значения F₁; F₂; F₃ и площади поперечных сечений А₁ и А₂ для своего варианта взять из таблицы 4 и схемы на рисунке 4

 

 

Таблица 4

Вариант	№ схемы	F1, кН	F2, кН	F3, кН	A1, см2	A2, см2	а, m
1	1				2	4
2	2				2	4
3	3				2	4
4	4				4	2
5	5	40	60	20	4	2	1
6	6				4	2
7	7				2	4
8	8				4	2
9	9				2	4
10	10				4	2

 Исходные данные к задаче 4

 

 

Рис. 3

 

 

 

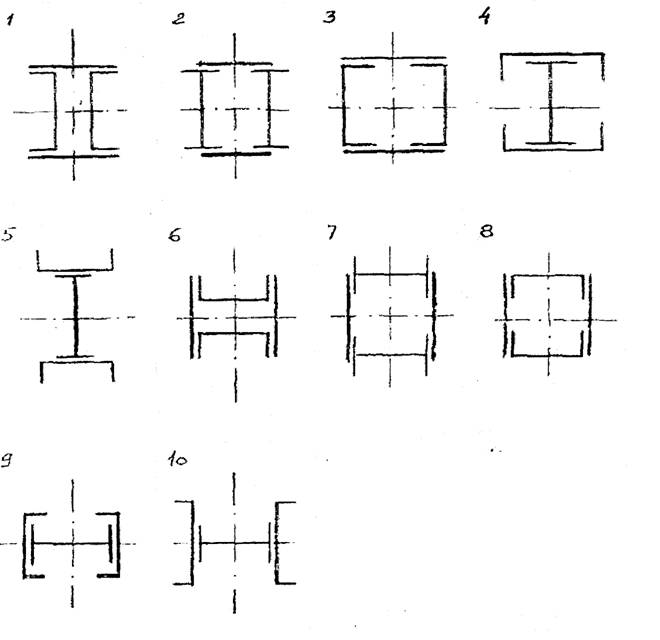
Рис. 4

           Методические указания по выполнению контрольной работы № 1

К задаче № 1.

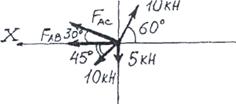
Определить усилия в стержневой системе АС и АВ, если к шарнирному болту А при­ложены силы Р₁, Р₂, Рз.  Р = 5 кН   (рис. 5)

 

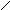
                        С

                                                                                     Р₃=2Р

                         В                       30^о      А  60^о

                                                     Р₂=2Р 45^о Р₁=Р             Рис.5

 

Решение:

1. Будем рассматривать равновесие шарнира А (точки А), так как к этому шарниру
приложены все силы.

2. Освобождаем точку А от связей (отбрасываем стержни АС и ВА) и заменяем их дей­
ствие реакциями F_Ac и Fab.

3. Таким образом, на точку А действуют силы:

 

• активные P₁, P₂, Рз (известные);

• реактивные Fac и Fab (неизвестные).
Действующие силы показаны на рисунке 9.

 

Рис. 6

Получили плоскую систему сходящихся сил, находящуюся в равновесии, действитель­ные направления сил Fac и Fab неизвестны. Принято предполагать, что стержни испытывают растяжение и направлять их реакции от узла (шарнира). Знак усилия, полученный в резуль­тате аналитического решения, подскажет истинное его направление: если усилие положи­тельное - направление предполагалось верным, отрицательное - направление противопо­ложно предполагаемому.

4. Определим искомые усилия двумя способами: аналитическим и геометрическим.

5. Аналитический способ. Выбираем систему координат и записываем равновесия       плоской системы сходящихся сил.

= F_AB +F_AC •cos30⁰+10·cos45°-10·cos60° =0

 = F_AC •sin30°+10-sin60⁰ -10·sin45° -5 = 0

Fac = 7 кН (растяжение)

F_AB + — + 2 = 0; Fab = -7,95 кН (сжатие)

Выбор системы координат и обозначение осей выполняется произвольно. Однако ра­циональный выбор осей может несколько упростить решение задачи. Желательно, чтобы возможно большее число неизвестных сил было перпендикулярно той или иной координат­ной оси. Уравнение равновесия получается проще (например, с одним неизвестным).

6. Геометрический способ (рис. 7). Полученная плоская система сходящихся сил на­ходится в равновесии, следовательно, силовой многоугольник, построенный на силах этой системы, должен быть замкнутым.

Строим силовой многоугольник. От точки О в выбранном масштабе откладываем в лю­бой последовательности известные силы Р_ь Р₂, Рз, совмещая начало последующей силы с концом предыдущей. После того, как отложены известные силы, получаем точку М.

Рис. 7

Через точку М проводим прямую, параллельную АС, а через точку О - прямую, парал­лельную АВ. Отрезки т. О и т. М представляют собой искомые усилия. Стрелки, изобра­жающие направления искомых сил, ставим так, чтобы в векторном многоугольнике было единое направление обхода.

Измерив отрезки т. О и т. М в соответствии с выбранным масштабом, находим абсо­лютные величины реакций.

Fa._b = 8кНF_AC = 7,2кН

Направление реакции Fac совпадает с предварительно выбранным (элемент АС дейст­вительно растянут), а направление реакции Fab - противоположно предварительно выбран­ному (элемент АВ - сжат).

7. Решение выполнено двумя способами, которые дали почти совпадающие результаты. Некоторые расхождения вызваны неточностью построения.

К задаче № 2 «а».

Рис. 8

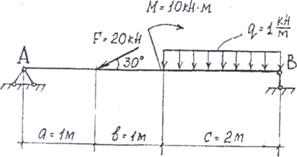
Определить реакции в опорах для балки (рис. 8)

 

Решение:

1. Рассматриваем равновесие балки АВ. Освобождаем балку от опор и заменяем их
действия реакциями (шарнирно-подвижную - одной, шарнирно-неподвижную - двумя вза­имно перпендикулярными).

2. Выбираем оси координат х и у.

3. Силу F раскладываем на две составляющие:

F_x = F·cos30°; F_y = F·sin30°.

                              

Y

 

Рис. 9

F_x = 20·cos30° = 20х0,87 = 17кН;

F_v = 20·sin30^о = 20x0,5 = 10кН.

4. Получили плоскую систему произвольно расположенных сил (рис. 9). Составляем уравнение статики, уравнения равновесия системы.

1) ∑М_А = F_ya + M – R_B(a + b + c) + q · c(a + b +с/2) = 0

10 + 10 – R_B(1 + 1 + 2) + 1 · 2(1 + 1 + 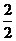) = 0

- R_B · 4 + 26 = 0 R_B = 6,5 кН

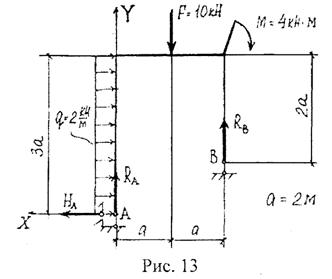
2) ∑М_В = - q · c · 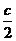 + M – F_y(c + b) + R_A(a + b + c) = 0

– 1 · 2 · 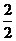 + 10 – 10(2 + 1) + R_A(1 + 1 + 2) = 0

R_A · 4 – 22 = 0 R_A = 5,5 кН

3) ∑x_i = F_x – H_A = 0

17 – H_A = 0  H_A = 17 кН

5. Проверяем правильность найденных результатов:

∑y_i= R_A + R_B – F_y – q – c = 0

5,5 + 6,5 – 10 – 1 – 2 = 0 0 = 0

Условие равновесия выполняется, следовательно, реакции опор найдены верно.

 

 

К задаче № 2 «б».

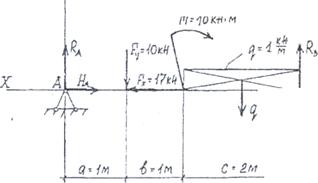
Определить реакции в опорах для рамы (рис. 10)

Решение:

1. Рассматриваем равновесие рамы АВ. Отбрасываем опорные закрепления и заменяем
их действие реакциями (шарнирно-подвижную - одной, шарнирно-неподвижную - двумя).

2. Выбираем оси координат х и у.

3. Получили плоскую систему произвольно-расположенных сил. Составляем уравнение
статики (уравнения равновесия системы).

 

1) ∑x_i = H_A – q · 3a = 0

H_A – 2 · 6 = 0; H_A = 12 кН

2) ∑М_А = q · 3a · l,5a + F · a + M – R_b ^. 2a = 0

2 ^. 6 · l,5 · 2 + 10 · 2 + 4 - R_b · 4  = 0; R_b = 60/4=15кН

3) ∑M_b =R_A · 2a – F_a ^. а + M + q · 3a · 0,5a + H_A · a = 0

R_A · 4 – 10 · 2 + 4 + 2 ^. 6 · 0,5 · 2 + 12 · 2 = 0;  

R_A =  -20/4 = -5кН

4. Проверяем правильность результатов, составив уравнение:

∑Y_i = R_A + R_b – F = 0

-5 +15 – 10 = 0                    0 = 0

Условия равновесия выполняется, следовательно, реакции опор найдены верно.

К задаче 3.

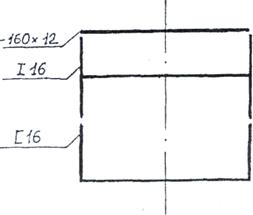
Определить главные центральные моменты инерции сечения, составленного из прокат­ных профилей (рис. 11).

 

Рис. 11

 

Решение:

1. Вычертим сечение в масштабе, взяв необходимые размеры и характеристики в таб­лицах сортамента (приложения 3,4).

2. Покажем на схеме сечения центры тяжести составных частей С_1,С_2,С₃(рис. 12).

 

 

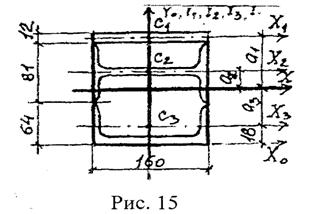
C₁ – центр тяжести прямоугольной полосы; С₂ – центр тяжести двутавра;

С₃ – центр тяжести швеллера.

Проводим центральные оси отдельных частей: x₁, x₂, x₃, y₁, y₂, y₃.

3. Определяем положение центра тяжести всего сечения в осях х_о; у_о (ось х_о выбраны произвольно, у_о - совмещена с осью симметрии сечения).

Так как сечение симметрично относительно оси у_о, то его центр тяжести расположен на этой оси.

Следовательно, координата х_с центра тяжести составного сечения равна нулю, коорди­нату у_с, определим по формуле:

 

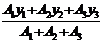
А₁, А₂, Аз — площади отдельных частей;

y₁ = 6,4 + 0,6 + 8,1 = 15,1 см; y₂ = 6,4 + 4,05 = 10,45 см; у₃ = 1,8 см.

 

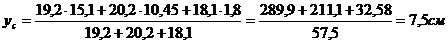
Показываем на чертеже центр тяжести сечения с (0; 7,5) и проводим через него главные центральные оси х и у.

4. Вычислим расстояние между главной центральной осью всего сечения х и централь­ными осями отдельных частей относительно оси х: а_1,а_2,а₃ и определим моменты инерции отдельных частей сечения

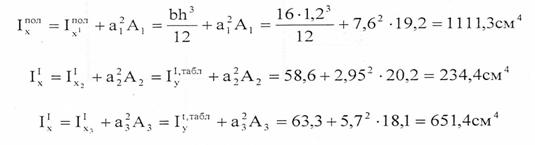
Таким образом, центральный осевой момент инерции сечения относительно оси х.

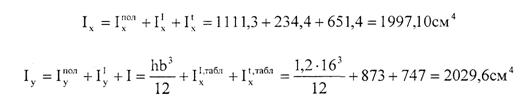
К задаче 4.

Двухступенчатый стальной брус нагружен силами F₁, F₂, F₃ (рис. 13). Построить эпюры продольных сил N и нормальных напряжений δ по длине бруса. Определить перемещение ∆ 1 свободного края бруса (Е = 2 х 10⁵ Н/мм²).

 

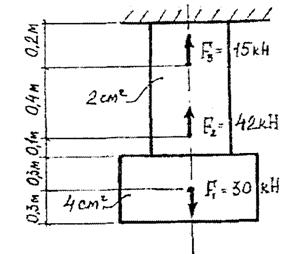
Рис. 13

 

Решение:

1. Разбиваем брус на участки, начиная от свободного края. Границами участков будут сечения, в которых приложены силы (рис. 14).

 

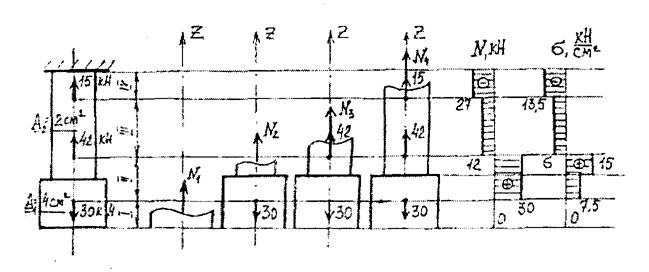
Рис. 14

Данный брус имеет 4 участка. В пределах каждого участка воспользуемся методом се­чений:

- Разбиваем брус на рассматриваемом участке сечением, перпендикулярным оси бруса;

- Мысленно отбрасываем любую часть бруса (лучше отбросить верхнюю часть с жест­
кой заделкой, чтобы не определять реакцию в заземлении);

- Заменяем влияние отброшенной части на оставленную внутренней силой Ni;

- Рассматриваем в равновесии оставленную (нижнюю) часть бруса под действием
внешних сил и внутренней силы Ni;

- Составляем уравнение равновесия (уравнение статики Z = 0) и, решив его, определяем
искомые внутренние силы.

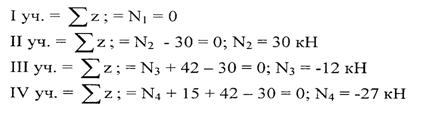
По найденным значениям строим эпюру продольных сил.

2. Вычисляем ординаты эпюры нормальных напряжений

 

 

Строим эпюру нормальных напряжений.

 

 

3. Определяем перемещение свободного края как алгебраическую сумму абсолютных удлинений (укорочений) отдельных участков:

 

(сжатие или укорочение)

 

Приложение 1