ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ. 4
1.1 Векторный, координатный и естественный способы задания движения точки 5
1.2. Скорость и ускорения движущейся точки при векторном способе задания ее движения. 6
1.3. Скорость и ускорение точки при координатном способе задания ее движения 7
1.4. Скорость и ускорение точки при естественном способе задания движения 8
1.5. Поступательное движение твердого тела. 9
1.6. Вращательное движение твердого тела вокруг неподвижной оси 10
1.7. Скорость и ускорение точек тела при вращательном движении 12
1.8. Плоскопараллельное движение твердого тела. 13
1.9. Определение скоростей точек плоской фигуры.. 14
1.10 Теорема о проекциях скоростей двух точек тела, движущего плоскопараллельно 16
1.11. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. 17
1.12. Некоторые частные случаи определения положения мгновенного центра скоростей 18
1.14. Сложное движение точки. 20
1.15 Теорема сложения скоростей и ускорений – при сложном движении точки 21
1.16 Ускорение Кориолиса. 22
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 24
ВВЕДЕНИЕ
Основной задачей настоящего методического указания является оказание помощи студенту заочной формы обучения при подготовке к аудиторной контрольной работе по разделу теоретической механики «Кинематика». При положительной оценке преподавателем результатов указанной контрольной работы студент будет допущен к сдаче зачета или экзамена по указанным разделам дисциплины «Теоретическая механика».
В контрольной работе содержаться два теоретических вопроса (один по разделу «Статика», второй по разделу «Кинематика») и одна задача на применение основных законов и принципов раздела «Статика» или «Кинематика».
В методических указаниях содержится минимум необходимый для ответов на теоретические вопросы материалов, а также примеры решения задач, тематика которых совпадает с тематикой задач, которые будут представлены при проведении аудиторной контрольной работы.
Рецензированию подлежат только те контрольные работы, в которых содержится ответ на один теоретический вопрос и дано решение предложенной задачи. Преподаватель оценивает полноту ответов на теоретические вопросы, правильность решения задачи и делает окончательное заключение о получении оценки «зачтено».
КИНЕМАТИКА
Векторный, координатный и естественный способы задания движения точки
Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Установление математических способов задания движения точек или тел является одной из важных задач кинематики.
Пусть точка М движется по отношению к некоторой системе отсчета Охуz (рис. 2.1).
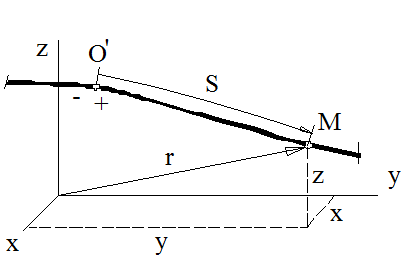
Рис.1.1
Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 
, проведенный из точки О в точку М.
При движении точки М данный вектор будет с течением времени изменяться по величине, и по направлению. Следовательно, он является переменным вектором (вектором-функцией), зависящим от времени t:
.
Это равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий радиус-вектор и найти положение движущейся точки в любой момент времени.
Если вместо зависимости 
будут заданы координаты х, у и z точки как функции времени
,
то такой способ задания движения точки будет называться координатным.
Если движение точки происходит в одной плоскости, то, приняв эту плоскость за плоскость Оху, получим два уравнения движения:
При прямолинейном движении точки, направив вдоль ее траектории координатную ось Ох, движение будет определяться одним уравнением
Естественным способом задания движения точки удобно пользоваться в случае, если известна траектория движущейся точки.
Движение точки считается описанным естественным способом, если известны (рис.2.1): траектория γ, дуговая координата 
, начало отсчёта (O /), положительное (+) направление отсчета S. Величина s в уравнении определяет положение движущейся точки на траектории, а не пройденный ею путь.
