Оценку погрешности результата измерения выполняют при разработке методики выполнения измерений (МВИ). Источниками погрешностей являются модель объекта измерений (ОИ), метод измерения (МВИ), средство измерения (СИ), оператор связи измеряемых и вычисляемых физических величин, влияющие факторы условий измерений, алгоритм обработки результатов наблюдений.
Как правило, погрешность результате измерения оценивается при доверительной вероятности Р - 0,95.
При выборе значения Р необходимо учитывать степень важности (ответственности) результата измерений. Например, если ошибка в измерении может привести к гибели людей или к тяжелым экологическим последствиям, значение Р должно быть увеличено.
1. Измерения с однократными наблюдениями. За результат измерения в этом случае принимают результат однократного наблюдения х (с введением поправки, если она имеется), используя предварительно полученные (например, при разработке МВИ) данные об источниках, составляющих погрешность.
Доверительные границы неисключенной систематической погрешности (НСП) результата измерения Ө(Р) вычисляют по формуле:
где k(P) - коэффициент, определяемый принятой Р и числом m, составляющих НСП: Ө(Р) - найденные нестатистическими методами границы j-ой составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале). При Р = 0,90 и 0,95 k(P) равен 0,95 и 1,1, соответственно при любом числе слагаемых Ш| При Р - 0,99 значения k(P) следующие (табл. 3.1):
Таблица 3.1. значения коэффициентов k(P)
| m | k(P) | m | k(P) |
| 5 и более | 1,45 | 3 | 1,3 |
| 4 | 1,4 | 2 | 1,2 |
Если составляющие НСП распределены равномерно и заданы доверительными границами Θ(Р), то доверительную границу НСП результата измерения вычисляют по формуле:
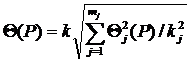, (3.1.)
где k и kj - те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности Р и Pj соответственно; mj - число составляющих НСП.
Среднеквадратическое отклонение (СКО) результата измерения с однократным наблюдением вычисляют одним из следующих способов.
Если в технической документации на СИ или в МВИ указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т.д.), то СКО вычисляют по формуле:
(3.2)
где m2 - число составляющих случайной погрешности; Sj - значения СКО этих составляющих.
Доверительную границу случайной погрешности результата измерения е(Р) в этом случае вычисляют по формуле:
e(P) = z p/2 S2j (x) (3.3.)
где Z p/2 - значение нормированной функции Лапласа в точке Р/2 при доверительной вероятности Р (табл. 3.2):
Таблица 3.2. значения нормированной функции Лапласа
| Р | Z p/2 | Р | Z p/2 |
| 0,90 | 1,65 | 0,97 | 2,17 |
| 0,95 | 1,96 | 0,98 | 2,33 |
| 0,96 | 2,06 | 0,99 | 2,58 |
2. Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами еj(Р) при одной и той же доверительной вероятности Р, то доверительную границу случайной погрешности результата измерения с однократным наблюдением пои доверительной вероятности вычисляют по формуле
(3.4)
3. Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений и N <30, то:
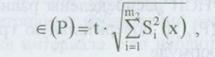(3.5.)
где t - коэффициент Стьюдента, соответствующий наименьшему числу наблюдений nj из всех N, можно найти в [4] или в любом справочнике по теории вероятностей; S(x) - оценки СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле (3.2). Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определено сразу суммарное СКО, то в формуле (3.2) m2 = 1.
4. Если случайные составляющие погрешности результата наблюдений представлены доверительными границами e(Pj), соответствующими
разным вероятностям Рj то сначала определяют СКО результата измерения с однократным наблюдением по формуле:
(3.5a)
Где Z p/2 - значение нормированной функции Лапласа в точке Р/2. Затем вычисляют e(P) по формуле 3.5.
Для суммирования систематической и случайной погрешностей рекомендуется следующий способ. Если 
, то НСП Θ(P) пренебрегают, и окончательно принимают έ(Р) за погрешность результата измерения Δ(Р) при доверительной вероятности Р. Если Θ(Р)/S(P) >0,8, то пренебрегают случайной погрешностью и принимают Δ(Р)= Θ(Р).
3.2. Измерения с многократными наблюдениями. Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах — это результат х „ отдельного наблюдения, входящего в ряд из N наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного.
При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое х результатов наблюдений х, по формуле:
.
Затем вычисляют оценку СКО результат наблюдений как
.
Далее находят Vn предполагаемого промаха xn от 
:
.
По числу всех наблюдений, (в том числе и хn), и принятому Р (обычно 0,95), находят Z(P,n) – нормированное выборочное отклонение нормального распределения. Если Vn < Z(P,n)*S, то наблюдение xn не является промахом.
Если Vn > Z(P,n)*S, то наблюдение xn - промах, подлежащий исключению.
После исключения промахов xn повторяют вычисление и S, для оставшегося ряда результатов наблюдений и повторяют проверку на промах наибольшего из оставшихся значений xn при новых значений N.
Доверительные границы Ө(Р) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением - по формулам (3.4).
Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении Δ(Р) рекомендуется осуществлять с использованием критериев и формул (3.6 - 3.8), в которых при этом S(x) заменяется на S(x) = S(x)/√n.
1. Косвенные измерения. Значение измеряемой величины А находят по результатам измерений аргументов а1, a2..., а,,...аm, связанных с искомой величиной уравнением:
.
Вид функции f определяется при установлении модели объекта измерения ОИ.
Косвенное измерение при линейной зависимости. Искомая величина А связана с т измеряемыми аргументами уравнением
где bj - постоянные коэффициенты.
Предполагается, что корреляция между погрешностями измерений а, отсутствует. Результат измерения А вычисляют по формуле
где ấ, — результат измерения а, с введенными поправками. Оценку СКО результата измерения S(A) вычисляют по формуле:
Где S(A) – оценка СКО результат измерений аj.
Доверительные границы e(P) случайной погрешности А при нормальном распределении погрешностей а:
где t(Р,nef) — коэффициент Стьюдента, соответствующий доверительной вероятности Р (обычно 0,95, в исключительных случаях 0,99) и эффективному числу наблюдений nef, вычисляемому по формуле
Здесь nj – число наблюдений при измерении а.
Доверительные границы Ө(Р) НСП результата такого измерения, сумму Ө(Р) и е(Р) для получения окончательного значения Δ(Р) рекомендуется вычислять с использованием критериев и формул (3.1), (3.2), (3.3), в которых m 1, Ө j, и S(x) заменяются, соответственно, на m, biӨi, и S(A).
Лекция 4
ИЗМЕРЕНИЯ. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
