Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется совместной, в противном случае – несовместной
1. Решение систем матричным методом.
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных
Пусть дана система уравнений
Рассмотрим матрицу составленную из коэффициентов при неизвестных:
.
Свободные члены и неизвестные можно записать в виде матриц-столбцов:
.
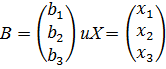Тогда, используя правило умножения матриц, эту систему уравнений можно записать так:
∙ 
= 
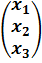или А∙В=Х.
(Решение матричных уравнений мы разбирали на прошлой лекции)
2. Решение систем методом Крамера.
Пусть дана система линейных уравнений
Составим матрицу составленную из коэффициентов при неизвестных:
.
Свободные члены и неизвестные запишем в виде матриц-столбцов:
.
Определитель матрицы А обозначим D и назовем определителем системы:
.
Пусть D ≠0
Если в определителе системы заменить поочередно столбцы коэффициентов при х1, х2, х3 на столбец свободных членов, то получим определители:
,
Тогда формулы Крамера для решения системы запишутся так:
.
Если D =0, то:
1) если каждый определитель Di =0, тогда, система имеет бесчисленное множество решений;
2) хотя бы один из Di ≠ 0, тогда система не имеет решений.
3. Решение систем методом Гаусса.
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы.
Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
Замечание. Диагональная матрица - это пример матрицы, которая является одновременно верхне- и нижнетреугольной.
Пример:
- верхнетреугольная матрица
Системы уравнений называются эквивалентными, если множество их решений совпадают.
Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов
Метод Гаусса - метод последовательного исключения неизвестных. Он состоит в следующем: систему уравнений 
приводят к эквивалентной ей системе с треугольной матрицей. 
Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратных ход).
При выполнения прямого хода используют следующие преобразования:
ü умножение или деление коэффициентов и свободных членов на одно и тоже число;
ü сложение и вычитание уравнений;
ü перестановку уравнений;
ü исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.
