Этапы решения задач на ЭВМ

Введение

 

     Информационные технологии в настоящее время являются одной из наиболее быстро развивающихся областей современной жизни. Развитие информационных технологий обусловливает и развитие программного обеспечения (ПО), как одной из важнейших своих составляющих. В создании ПО значительную роль играет уровень возможностей средств общения человека с ЭВМ. Во многом этот уровень определяется языками программирования (ЯП).

    Первые ЯП представляли собой набор машинных команд в двоичном (бинарном) или восьмеричном формате, который определялся архитектурой конкретной ЭВМ. Каждый тип ЭВМ имел свой ЯП, программы на котором были пригодны только для данного типа ЭВМ. От программиста при этом требовалось хорошее знание не только машинного языка, но и архитектуры ЭВМ.

     Следующий этап развития ЯП характеризуется созданием языков ассемблерного типа, позволяющих вместо двоичных форматов машинных команд использовать их мнемонические символьные обозначения (имена). Являясь существенным шагом вперед, ассемблерные языки все еще оставались машинно-зависимыми, а программист все также должен был быть хорошо знаком с организацией и функционированием аппаратной среды конкретного типа ЭВМ. При этом ассемблерные программы также затруднительны для чтения, трудоемки при отладке и требуют больших усилий для переноса на другие типы ЭВМ.

     Языки высокого уровня (ЯВУ) открывают третье поколение ЯП. Основная черта высокоуровневых языков - введение смысловых конструкций, кратко описывающих целые структуры данных и операции над ними. Первый ЯВУ - Fortran - был разработан под руководством Дж. Бэкуса в фирме IBM в 1956 г.

     ЯВУ характеризовались следующими чертами:

- от пользователя не требуется знания машинного языка;

- язык не связан с определенным типом ЭВМ, поэтому обеспечивает перевод программ с одной ЭВМ на другую;

- одна инструкция ЯВУ переводится в несколько команд машинного кода;

- выражения языка соответствуют области его применения.

    Таким образом, можно сделать следующие выводы:

     1. Языки низкого уровня исторически появились первыми. Команды этих языков выполняют простейшие операции по обработке информации: сложение, вычитание, умножение, деление и т.д. Программы для решения большинства даже самых простых задач состоят из нескольких десятков или сотен таких команд. Работать с такой программой человеку очень трудно. В то же время, языки низкого уровня позволяют писать наиболее эффективные программы.

    2. Языки высокого уровня близки к языку математики и разговорному (традиционно - английскому). В этих языках:

- формулы записываются на языке, близком к математическому, с явным указанием всех операций;

- используется ограниченное количество типовых конструкций (вычисление по формулам, принятие решения, повторение, цикл, процедуры и т.п.);

- для выполнения на ЭВМ программы преобразуются на машинный язык с помощью самой ЭВМ.

 

Этапы решения задач на ЭВМ

 

     Решение задач на ЭВМ состоит из следующих этапов:

 

- постановка задачи;

- математическая формализация;

- построение алгоритма;

- составление программы на языке программирования;

- отладка и тестирование программы;

- анализ полученных результатов.

 

    Этап постановки задачи включает формулировку условия задачи, определение конечных целей решения задачи, описание исходных данных (их типов, диапазонов возможных значений, структуры и т. п.), определение формы выдачи результатов. На этом этапе должно быть четко определено, что известно и что требуется получить в результате.

    Этап математической формализации включает выбор математических методов и моделей, запись формул, обеспечивающих решение задачи, составление плана решения.

     Этап построения алгоритма предполагает формирование строгой и четкой системы правил, определяющей последовательность действий, которая за конечное число шагов должна привести к результату.

     Этап составления программы включает следующие шаги: выбор языка программирования; уточнение способов организации данных; запись алгоритма на выбранном языке программирования.

     Под отладкой программы понимается процесс испытания работы программы и исправления обнаруженных при этом ошибок.

Возможны программные ошибки трех видов:

- синтаксические (ошибки в правилах языка);

- алгоритмические (ошибки в логике программы);

- ошибки времени исполнения, возникающие в процессе работы запущенной программы.

Компилятор способен найти только синтаксические ошибки, для выявления же алгоритмических ошибок служит этап тестирования программы. Ошибки времени исполнения возникают как результат некорректных действий пользователя, недопустимых операций над данными (например, попытки извлечь квадратный корень из отрицательного числа, поделить на ноль) или ошибок программного и аппаратного обеспечения ЭВМ.

    Анализ полученных результатов – последний этап, на котором делается вывод о возможности применения разработанной программы для получения искомых результатов. Кроме того, на этом этапе могут быть сделаны выводы о некорректности постановки задачи или разработанной математической модели.

 

    1.2. Алгоритм. Свойства алгоритмов.

 

     Алгоритм – это точное предписание о выполнении в определенном порядке некоторых операций, приводящих к решению всех задач данного класса. Другими словами, алгоритмом можно назвать однозначно определенную последовательность действий, записанную на понятном исполнителю алгоритмическом языке и определяющую процесс перехода от исходных данных к результату.

       Свойства алгоритма:

1) определенность (точность предписаний и однозначность результата);

2) массовость (ориентированность на класс задач, например, решение системы произвольного количества уравнений при любых исходных данных);

3) дискретность (деление процесса решения на этапы, понятные человеку и ЭВМ);

4) результативность (за конечное число шагов достигается некоторый результат);

5) конечность - заключается в том, что последовательность элементарных действий алгоритма не может быть бесконечной, неограниченной, хотя может быть очень большой (если требуется, например, большая точность вычислений);

6) корректность - означает, что если алгоритм создан для решения определенной задачи, то для всех исходных данных он должен всегда давать правильный результат и ни для каких исходных данных не будет получен неправильный результат.

    Программа - это реализация алгоритма на конкретном языке программирования.

     Схемы алгоритмов и программ входят в состав программной документации и оформляются в соответствии с ГОСТ 19.701 – 90 (ИСО 5807 – 85) "Схемы алгоритмов, программ, данных и систем" (взамен ГОСТ 19.002-80, 19.003-80). При этом используются условные графические обозначения (УГО), которые вписываются в прямоугольник (см. рис. 1.1). Стороны прямоугольника имеют следующие размеры:

a = 10, 15, 20 и т.д. через 5 мм,    b = 1,5а или b = 2a.

Наиболее часто используемые блоки приведены в табл. 1.

Таблица 1 Блоки для изображения схем алгоритмов и программ

 

Наименование	Обозначение	Действие
Процесс		Выполнение любых операций по обработке данных, например, вычисления по формуле
Решение		Выбор направления выполнения алгоритма в зависимости от условия
Ввод – вывод		Ввод – вывод данных. Внутри блока – имена переменных
Дисплей		Представление данных на дисплее при выводе. Внутри записывают имена выводимых переменных
Документ		Вывод данных на бумажный носитель. Внутри записывают имена выводимых переменных
Пуск – останов
Соединитель		Связь между прерванными линиями схемы
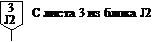Межстраничный соединитель		Связь между блоками на разных листах

 

Схема алгоритма представляет собой совокупность УГО, соединенных линиями связи. Схема начинается блоком "Начало" и заканчивается блоком "Конец". Для каждого элемента схемы должно выполняться условие:существует, по крайней мере, один путь от блока "Начало" до блока "Конец", проходящий через этот элемент.

 

     Тема 2. Базовые алгоритмические конструкции

        

    Вопросы темы:

 

1. Алгоритмическая конструкция «следование».

2. Алгоритмическая конструкция «ветвление».

3. Алгоритмическая конструкция «цикл».

 

Все алгоритмы традиционно можно разделить на три основных типа.

 

1. Линейный, который предполагает естественный порядок выполнения (следования) блоков ввода, процесса и вывода, т.е. действия осуществляются

последовательно друг за другом.

 

                      Рис. 1.2. Схема линейного алгоритма.

 

  2. Разветвляющийся, который задает выполнение вычислений по одному из возможных направлений, в зависимости от исходных данных или промежуточных результатов, т.е. действие выполняется по одной из возможных ветвей решения задачи, в зависимости от выполнения условий. В отличие от линейных алгоритмов, в которых действия выполняются последовательно, в разветвляющиеся алгоритмы входит условие, в зависимости от выполнения или невыполнения которого производится та или

иная последовательность действий.

   В качестве условия в разветвляющемся алгоритме может быть использовано любое понятное исполнителю утверждение, которое может соблюдаться (быть истинно) или не соблюдаться (быть ложно). Такое утверждение может быть выражено как словами, так и формулой. Таким образом, алгоритм ветвления состоит из условия и двух последовательностей команд. Пример такого алгоритма показан на следующем рисунке 1.3.

            Рис. 1.3. Схема разветвляющегося алгоритма

 

   3. Циклический, который содержит многократно повторяющиеся участки (циклы). Здесь некоторая часть операций (тело цикла - последовательность команд) выполняется многократно. 

   Перед операцией цикла осуществляются операции присвоения

начальных значений тем объектам, которые используются в теле цикла. В цикл входят в качестве базовых следующие структуры: блок проверки условия и блок, называемый телом цикла. Если тело цикла расположено после проверки условия (цикл с предусловием), то может случиться, что

при определенных условиях тело цикла не выполнится ни разу. Такой вариант организации цикла, управляемый предусловием, называется цикл типа пока (здесь условие - это условие на продолжение цикла).

    Возможен другой случай, когда тело цикла выполняется по крайней мере один раз и будет повторяться до тех пор, пока не станет истинным условие. Такая организация цикла, когда его тело расположено перед проверкой условия, носит название цикла с постусловием, или цикла типа

                          Рис. 1.4. Схема циклического алгоритма.

до. Истинность условия в этом случае - условие окончания цикла.Итак, цикл до завершается, когда условие становится истинным, а цикл пока -когда условие становится ложным.

     Циклические алгоритмы, в которых тело цикла выполняется заданное число раз, реализуются с помощью цикла со счетчиком. Цикл со счетчиком реализуется с помощью рекурсивного увеличения значения счетчика в теле цикла.

                   

  На рис. 1.4. показан пример циклического алгоритма для вычисления значения функции

Y=Sin(X)

для аргумента, изменяющегося в диапазоне от Xn до Xk с шагом h.