Количество движения. Момент количества движения
Количество движения МТ в пространстве Oxyz –
.
Количество движения МТ по направлению l –
.
Момент количества движения (кинетический момент) МТ относительно центра О –
.
Для МСМТ количество движения
,
или используя центр масс
.
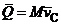Кинетический момент 
вычисляется по аналогии с моментом силы 
относительно центра О: кинетический момент МТ относительно центра О направлен перпендикулярно плоскости, в которой расположены векторы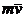 
и 
, а модуль его равен
,
где h - плечо количества движения относительно центра момента О. Приложен вектор к точке О.
Момент количества движения МТ Kz относительно оси Oz (как в статике) равен проекции на эту ось момента количества движения точки относительно центра О, расположенного на этой оси
.
Для МСМТ кинетический момент
,
.
Кинетическая энергия
Кинетическую энергию МТ массой m, движущейся со скоростью 
, определяют по формуле
.
Кинетическая энергия МСМТ
.
Кинетическая энергия ТТ:
, где - скорость частицы тела (γ) массы d m.
При поступательном движении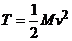 
,
при вращательном движении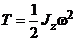 
,
при плоском движении (поступательное движение центра масс + вращение вокруг оси z C)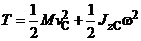 
.
Работа и мощность силы
Понятие «работа силы» характеризует действие силы на тело на некотором его перемещении.
При движении частицы М под действием силы за меру действия силы на пути dS принимают элементарную работу силы δ А:
.
, 
, отсюда 
.
Таким образом, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.
Работа силы тяжести: 
, 
- высота опускания (+) или поднимания (-) груза.
Работа силы тяжести не зависит от формы траектории между начальной и конечной точкой, и если эти точки совпадают, то работа силы тяжести равна нулю. Работа равна нулю и если траектория движения лежит в одной и той же горизонтальной плоскости.
Работа линейной силы упругости:
Линейной силой упругости называют силу, действующую по закону Гука,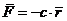 
,
где - радиус-вектор от произвольного положения точки до точки статического равновесия (то есть до точки, в которой эта сила равна нулю), с - коэффициент жесткости упругого элемента.
Если начало координат в точке статического равновесия, то сила упругости в проекциях на координатные оси: 
, 
, 
.
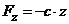Работа силы упругости: 
. Работа силы на перемещении от произвольной точки M0 до точки М: 
, где - расстояние между точкой M и точкой статического равновесия.
Работа сил трения:
Трение скольжения:
, G – вес тела, f – коэффициент трения скольжения.
Трение качения:
, G – вес тела, k – коэффициент трения качения.
Мощность силы – работа силы в единицу времени, 
.
В векторной, координатной и естественной формах
,
,
.
Мощность силы и пары сил, приложенных к ТТ
Мощность силы 
, приложенной в точке М k тела
,
где А – полюс. Иначе
,
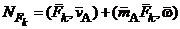- момент силы относительно полюса.
Мощность пары сил 
.
При поступательном движении
, 
.
При вращательном движении
, 
.
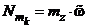При плоском движении
, 
,
А – полюс фигуры, P - мцс.
ОБШИЕ ТЕОРЕМЫ ДИНАМИКИ
Теорема о движении центра масс МС
Центр масс МСМТ движется как МТ с массой, равной массе системы, под действием силы, равной главному вектору всех внешних сил, приложенных к точкам системы:
.
Следствия (закон сохранения движения центра масс):
1) действием одних только внутренних сил нельзя изменить движение центра масс МСМТ;
2) если главный вектор внешних сил равен нулю или равна нулю его проекция на какое-либо направление, то в первом случае центр масс системы находится в покое или движется равномерно и прямолинейно, а во втором случае сохраняется движение центра масс по этому направлению.
