КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
При движении абсолютно твердого тела (АТТ) в общем случае отдельные его точки движутся по различным траекториям и имеют в каждый момент времени различные скорости и ускорения. Движение твердого тела считается заданным, если имеется способ определения положения любой его точки в любой момент времени по отношению к выбранной системе отсчета.
Основными задачами кинематики АТТ являются:
1) задание движения АТТ;
2) определение кинематических характеристик АТТ;
3) определение траекторий, скоростей и ускорений всех точек АТТ.
Поступательное движение абсолютно твердого тела
Поступательным называют такое движение АТТ, при котором любая прямая, жестко скрепленная с телом, перемещается, оставаясь параллельной самой себе.
Закон движения. Для задания поступательного движения АТТ достаточно задать движение некоторой его точки А - полюса. Закон поступательного движения АТТ - это закон движения полюса:
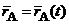- в векторной форме; 
— в координатной форме.
Кинематические характеристики - скорость тела 
, равная скорости полюса, и ускорение тела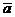 
, равное ускорению полюса.
Скорость и ускорение произвольной точки поступательно движущегося АТТ равны скорости и ускорению полюса.
Если уравнение движения 
, то 
, 
.
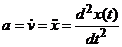Вращательное движение абсолютно твердого тела вокруг неподвижной оси
Вращательным вокруг неподвижной оси называют движение АТТ, имеющего две
неподвижные точки. Прямая, проходящая через эти две точки, называется осью вращения.
Траектории всех точек представляют собой окружности.
Закон движения. Положение тела полностью определено, если задан угол 
- угол поворота АТТ. Закон вращательного движения - .
Кинематические характеристики – угловая скорость 
, (
- алгебраическая величина), угловое ускорение 
. Векторы угловой скорости и углового ускорения направлены вдоль оси вращения.
Скорость и ускорение произвольной точки.
Для произвольной точки M на расстоянии R от оси вращения ее алгебраическая скорость 
. Вектор скорости направлен в сторону вращения по касательной к траектории движения. Ускорение точки 
- сумма касательного и нормального ускорений,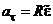 
, 
, 
.
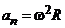→ Задача К2.
Плоское движение абсолютно твердого тела
Плоским называют такое движение АТТ, при котором каждая его точка все время движется в одной и той же плоскости. Траектории точек – плоские кривые.
Закон движения.
Выбирают отрезок АВ, выбирают за полюс точку А, связывают с фигурой систему координат A x 1 y 1. Положение отрезка относительно системы координат O XY определяется задание координат x A, y A, φ. Закон движения: 
, 
, .
Кинематические характеристики: скорость полюса 
, угловая скорость АТТ , ускорение полюса 
, угловое ускорение АТТ 
.
, 
, 
, 
.
Скорость и ускорение произвольной точки.
1 способ определения:
, скорость любой точки складывается из скорости полюса и скорости точки в круговом движении вокруг полюса; 
.
, ускорение любой точки складывается из ускорения полюса и ускорения точки в круговом движении вокруг полюса; 
, 
, 
.
2 способ определения:
Плоское движение АТТ может быть представлено как мгновенно вращательное движение с угловой скоростью вокруг некоторой точки, скорость которой в данный момент времени равна 0 – мгновенный центр скоростей P. 
, отсюда угловая скорость фигуры 
.
Способы определения положения МЦС: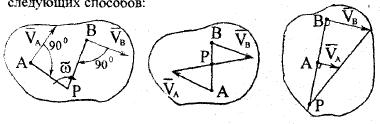 
Для определения ускорения используют мгновенный центр ускорений – точка Q, в которой в данный момент времени ускорение равно 0. 
.
Способы определения положения МЦУ:
1) от ускорения под углом 
в сторону ε отложить отрезок 
.
2) Повернуть ускорения двух известных точек на угол μ в сторону ε, на пересечении будет МЦУ.
3) Когда ε = 0, от точки А вдоль ускорения отложить отрезок 
.
4) Когда ω = 0, из точки А под углом μ = 90° в сторону ε отложить отрезок 
.
→ Задача К3.
