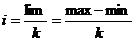1. Выбрать на листе Excel ячейки и ввести в них данные с омменариями
2. Последовательно решать задачу: выполнять действия, расчеты и вносить комментарии к ячейкам, в которых производились расчеты
3. Выделить ячейки с результатами (цветом, шрифтом и др.) и написать вывод


Рис. Два способа размещения компьютерной модели на листе Excel
Задание №1
В Excel создать компьютерную модель решения задачи построения таблицы ранжированием данных.
| Действия | Пояснения и визуализация действий | ||||||||||
| 1.Ввести в блок листа Excel данные эксперимента (n=10 – размер выборки) в столбец | Вес новорожденных при рождении был равен (в кг): 3,3; 3,1; 3,2; 4,2; 3,4; 3,0; 3,8; 3,3; 3,2; 4,2. | ||||||||||
| 2.Копировать данные в соседний столбец. Применить к данным процедуру ранжирования Данные-Сортировка | 
| ||||||||||
| 4.По результатам ранжирования построить таблицу, которая является результатом группировки |
|
Сущность ранжирования состоит в том, что варианты располагаются в строгом порядке по принципу их увеличения или уменьшения (т.е. по ранжиру). Минимальный вес новорожденных 3,0 кг, максимальный – 4,2 кг.
Группировка методом построения вариационных рядов.
Для больших выборок (n>30) основным методом группировки является построение ряда распределения. Каждая пара числовых рядов, составленная в результате группировки по одному признаку, называется рядом распределения. Если признак качественный, то ряд называется атрибутивным; если признак количественный – ряд вариационный.
Вариационным рядом называется двойной ряд, отражающий распределение количественных вариант по классам. При составлении вариационного ряда значения, которые принимает признак, называют классами (x), а количество вариант в классе – частотами (p). Сумма частот по всем классам должна равняться объему выборки (n). В математическом выражении это записывается так: Sp = n.
Вариационные ряды могут быть дискретными и непрерывными в зависимости от того, какой признак лежит в основе группировки – дискретный или непрерывный. Вариационные ряды, построенные на основе непрерывного признака, всегда – интервальные. Интервальными могут быть и ряды, в основе которых лежат дискретные признаки.
Например.
| Число смежных специальностей x | 1 - 2 | 3 - 4 | 5 – 6 |
| Число рабочих p | 229 | 113 | 55 |
Это интервальный ряд. Интервалы имеют верхнюю и нижнюю границы 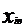 и
и  .
.
В вариационном ряду, преобразованном в интервальный из ряда, построенного на основе дискретного признака, может быть утрачена часть первичной информации. Предыдущий ряд был получен из следующего с потерей информации. Поэтому последующая обработка данных даёт лишь приблизительные результаты.
| Число смежных специальностей x | 1 | 2 | 3 | 4 | 5 | 6 |
| Число рабочих p | 105 | 124 | 68 | 45 | 17 | 38 |
Для интервальных распределений вводится показатель плотность распределения – частота, приходящаяся на единицу величины интервала - 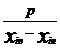 .
.
Задание №2
В Excel создать компьютерную модель решения задачи построения вариационного ряда.
| Действия | Пояснения и визуализация действий | ||||||
| 1. При взвешивании 50 спортсменов получены следующие данные (в кг): ввести данные в столбец. Слева в столбце пронумеровать данные. | 58 50 53 53 50 61 58 58 57 52 49 51 63 55 50 57 66 46 60 53 58 53 50 54 50 51 67 47 52 47 47 54 59 54 53 57 52 50 46 56 42 55 52 57 54 56 50 59 49 54 | ||||||
| 2. Для составления вариационного ряда необходимо: Найти в данных максимальное (max) и минимальное (min) значения признака. Разница между максимальным и минимальным значениями признака (варианта) – это размах изменчивости признака (lim = max–min). Исходя из объема выборки и размаха изменчивости, выбрать оптимальное число классов (k) для проведения группировки | Число наблюдений Число классов 40–60 6–10 61–100 7–10 101–200 9–12 201–500 12–17 В нашем примере число измерений равняется 50. Значит, число классов должно быть в пределах 6–10. В этих пределах подбирать число классов следует таким образом, чтобы величина классового промежутка была удобной для подсчета и, желательно, оканчивалась на цифру 5 или 0. Оформление Min= Max= Lim= K= | ||||||
| 3. На основании выбранного количества классов и размаха изменчивости признака установить величину классового промежутка (i), т.е. величину, на которую один класс должен отличаться от другого: |
max = 67; min = 42; lim = 25; k = 8 (подобранное нами число классов = 8)
- длина интервала (величина класса) | ||||||
| 4.Создать и заполнить таблицу. Началом первого класса обычно служит варианта с минимальным значением признака, концом первого класса – величина, равная началу первого класса, увеличенному на классовый промежуток (i). Конец последнего класса завершается максимальным значением варианты. Конец предыдущего и начало следующего классов должны совпадать. | 
| ||||||
| 5.Подсчитать частоты попадания данных в интервалы с помощью функции СЧЁТЕСЛИ. Сумма всех частот должна равняться объему выборки. | СЧЁТЕСЛИ(диапазон;критерий) Диапазон — диапазон, в котором нужно подсчитать ячейки. Критерий — критерий в форме числа, выражения, ссылки на ячейку или текста, который определяет, какие ячейки надо подсчитывать. Количество ячеек со значениями, большими или равным 32 и меньшими или равными 85 из диапазона B2:B5 равно =СЧЕТЕСЛИ(B2:B5,">=32")-СЧЕТЕСЛИ(B2:B5,">85") |
Задание №3
Решить задачу из задания №2, используя другой подход к выбору оптимальной величины интервала.
Для выбора оптимальной величины интервала, при котором вариационный ряд не будет громоздким и в нём не исчезнут особенности явления, также используют формулу Стерджеса: i = (хmax - xmin)/(1 + 3,2lnn) (в нашем примере = (хmax - xmin)/(1+3,2х3,9)= (хmax - xmin)/12,5=2), где n- число единиц совокупности, хmax, xmin - соответственно максимальное и минимальное значения совокупности, i - величина интервала (длина интервала, величина класса).
Задание №4
В Excel создать компьютерную модель решения задачи построения вариационного ряда для данных эксперимента, придумав название признака и определив единицы его измерения
8, 33, 30, 43, 39, 22, 7, 49, 41,11, 39,34,39,16, 22, 14, 10, 21, 6, 5, 47, 14, 43, 37, 5, 15, 48, 29, 10, 49, 9, 29, 39, 45, 16, 10, 28, 48, 40, 46, 22, 15, 33, 36, 36, 29, 42, 13, 38, 33, 44, 9,47,17, 46, 34, 32, 22, 14, 45, 9, 38, 32, 43, 48, 10, 36, 48, 31, 28, 46, 25, 27, 11, 25
| Действия | Пояснения и визуализация действий | |||
| 1.Ввести данные эксперимента (n=75) в блок листа Excel | 8, 33, 30, 43, 39, 22, 7, 49, 41,11, 39,34,39,16, 22, 14, 10, 21, 6, 5, 47, 14, 43, 37, 5, 15, 48, 29, 10, 49, 9, 29, 39, 45, 16, 10, 28, 48, 40, 46, 22, 15, 33, 36, 36, 29, 42, 13, 38, 33, 44, 9,47,17, 46, 34, 32, 22, 14, 45, 9, 38, 32, 43, 48, 10, 36, 48, 31, 28, 46, 25, 27, 11, 25 | |||
| 2.Если значения данных эксперимента разделить в Word вместо запятой знаком табуляции (инициируется клавишей Tab), то можно их поместить в блок ячеек листа Excel с помощью буфера обмена: Выделить – Копировать - Вставить | Например
8 33 30 43 39 22
7 49 41 11 39
34 39 16 22 14

| |||
| 3.Для определения величины класса используем формулу: i = (хmax - xmin)/(1 + 3,2lnn) | Для этого нужно найти: хmax xmin Lnn = Ln75 = 4,32 | |||
| 4.Для определения хmax и xmin используем в Excel строку состояния. Если выделить блок чисел, то в строке состояния отображается информация о выделенном блоке: максимальное или минимальное число, сумма, количество элементов. Какая именно информация выводится задает пользователь при помощи контекстного меню (щелкнуть правой кнопкой на строке состояния и выбрать) | 

| |||
| 5.Находим хmax и xmin | ||||
| 6.Подбираем число классов: k=7-10 | ||||
| 7.Находим величину классового промежутка |
| |||
| 8/Заполняем первую строку таблицы, в которой будет представлен наш вариационный ряд (у каждого своя) | ||||
| 9.Теперь надо заполнить вторую строку таблицы. Для этого используем функцию СЧЁТЕСЛИ | СЧЁТЕСЛИ(диапазон; критерий) Диапазон — диапазон, в котором нужно подсчитать ячейки. Критерий — критерий в форме числа, выражения, ссылки на ячейку или текста, который определяет, какие ячейки надо подсчитывать. Количество ячеек со значениями, большими или равным 32 и меньшими или равными 85 из диапазона B2:B5 = =СЧЕТЕСЛИ(B2:B5,">=32")-СЧЕТЕСЛИ(B2:B5,">85") | |||
| В первую ячейку набираем следующую формулу. Предполагаем, что в P16:W24 этот блок ячеек содержит данные эксперимента. Соответственно заполняем и другие ячейки. Сумма заполненных ячеек должна равняться n=75 | 
|
Вывод. Группировка статистического материала даёт возможность судить о структуре объекта исследования, о связях и зависимостях между явлениями и их признаками внутри изучаемых совокупностей. Для применения других статистических методов обработки и анализа группировка является необходимым подготовительным этапом. В основу группировки кладутся существенные признаки. Деление признаков на основные и неосновные зависит от задач и условий исследований.
Контрольные вопросы
1. Задачи статистического моделирования
2. Для чего нужны статистические таблицы
3. Подлежащее и сказуемое
4. Классификации таблиц
5. Методы создания статистических таблиц
6. Компьютерная модель решения задачи в Excel
7. Вариационные ряды и методы их построения
8. Функция СЧЁТЕСЛИ